何为最短路径
最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径,大致可以分为如下几种问题,可无论如何分类问题,其本质思想还是不变的,即,求两点间的最短距离。
a) 确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题。
b) 确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
c) 确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径。
d) 全局最短路径问题 - 求图中所有的最短路径。
迪杰斯特拉算法介绍
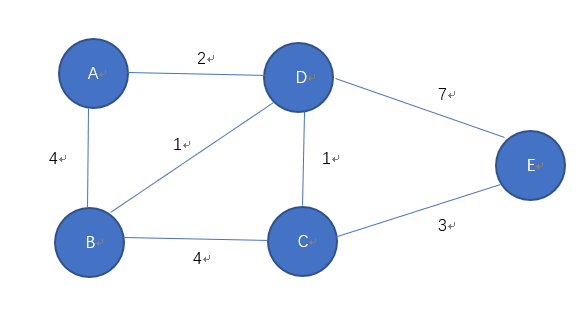
如上图,迪杰斯特拉算法的核心思路是:
1) 指定一个节点,例如我们要计算 'A' 到其他节点的最短路径
2) 引入两个集合(S、U),S集合包含已求出的最短路径的点(以及相应的最短长度),U集合包含未求出最短路径的点(以及A到该点的路径,注意 如上图所示,A->C由于没有直接相连 初始时为∞)
3) 初始化两个集合,S集合初始时 只有当前要计算的节点,A->A = 0,
4) U集合初始时为 A->B = 4, A->C = ∞, A->D = 2, A->E = ∞
5) 从U集合中找出路径最短的点,加入S集合,例如 A->D = 2
6) 更新U集合路径,if ( 'D 到 B,C,E 的距离' + 'AD 距离' < 'A 到 B,C,E 的距离' ) 则更新U
7) 循环执行 4、5 两步骤,直至遍历结束,得到A 到其他节点的最短路径
样例代码

#include <iostream>
#include <iomanip>
#include <string>
using namespace std;
#define INFINITY 65535//无边时的权值
#define MAX_VERTEX_NUM 10//最大顶点数
typedef struct MGraph {
string vexs[10];//顶点信息
int arcs[10][10];//邻接矩阵
int vexnum, arcnum;//顶点数和边数
} MGraph;
int LocateVex(MGraph G, string u) { //返回顶点u在图中的位置
for(int i=0; i<G.vexnum; i++)
if(G.vexs[i]==u)
return i;
return -1;
}
void CreateDN(MGraph &G) { //构造有向网
string v1, v2;
int w;
int i, j, k;
cout<<"请输入顶点数和边数:";
cin>>G.vexnum>>G.arcnum;
cout<<"请输入顶点:";
for(i=0; i<G.vexnum; i++)
cin>>G.vexs[i];
for(i=0; i<G.vexnum; i++)
for(j=0; j<G.vexnum; j++)
G.arcs[i][j]=INFINITY;
cout<<"请输入边和权值:"<<endl;
for(k=0; k<G.arcnum; k++) {
cin>>v1>>v2>>w;
i=LocateVex(G, v1);
j=LocateVex(G, v2);
G.arcs[i][j]=w;
}
}
//迪杰斯特拉算法求有向网G的v0顶点到其余顶点v的最短路径p[v]及带权长度D[v]
//p[][]=-1表示没有路径,p[v][i]存的是从v0到v当前求得的最短路径经过的第i+1个顶点(这是打印最短路径的关键),则v0到v的最短路径即为p[v][0]到p[v][j]直到p[v][j]=-1,路径打印完毕。
//final[v]为true当且仅当v∈S,即已经求得从v0到v的最短路径。
void ShortestPath_DIJ(MGraph G, int v0, int p[][MAX_VERTEX_NUM], int D[]) {
int v, w, i, j, min;
bool final[10];
for(v=0; v<G.vexnum; v++) {
final[v]=false;//设初值
D[v]=G.arcs[v0][v];//D[]存放v0到v得最短距离,初值为v0到v的直接距离
for(w=0; w<G.vexnum; w++)
p[v][w]=-1;//设p[][]初值为-1,即没有路径
if(D[v]<INFINITY) { //v0到v有直接路径
p[v][0]=v0;//v0到v最短路径经过的第一个顶点
p[v][1]=v;//v0到v最短路径经过的第二个顶点
}
}
D[v0]=0;//v0到v0距离为0
final[v0]=true;//v0顶点并入S集
for(i=1; i<G.vexnum; i++) { //其余G.vexnum-1个顶点
//开始主循环,每次求得v0到某个顶点v的最短路径,并将v并入S集,然后更新p和D
min=INFINITY;
for(w=0; w<G.vexnum; w++)//对所有顶点检查
if(!final[w] && D[w]<min) { //在S集之外(即final[]=false)的顶点中找离v0最近的顶点,将其赋给v,距离赋给min
v=w;
min=D[w];
}
final[v]=true;//v并入S集
for(w=0; w<G.vexnum; w++) { //根据新并入的顶点,更新不在S集的顶点到v0的距离和路径数组
if(!final[w] && min<INFINITY && G.arcs[v][w]<INFINITY && (min+G.arcs[v][w]<D[w])) {
//w不属于S集且v0->v->w的距离<目前v0->w的距离
D[w]=min+G.arcs[v][w];//更新D[w]
for(j=0; j<G.vexnum; j++) { //修改p[w],v0到w经过的顶点包括v0到v经过的所有顶点再加上顶点w
p[w][j]=p[v][j];
if(p[w][j]==-1) { //在p[w][]第一个等于-1的地方加上顶点w
p[w][j]=w;
break;
}
}
}
}
}
}
int main() {
int i, j;
MGraph g;
CreateDN(g);
int p[MAX_VERTEX_NUM][MAX_VERTEX_NUM];//最短路径数组p
int D[MAX_VERTEX_NUM];//最短距离数组D
ShortestPath_DIJ(g, 0, p, D);
cout<<"最短路径数组p[i][j]如下:"<<endl;
for(i=0; i<g.vexnum; i++) {
for(j=0; j<g.vexnum; j++)
cout<<setw(3)<<p[i][j]<<" ";
cout<<endl;
}
cout<<g.vexs[0]<<"到各顶点的最短路径及长度为:"<<endl;
for(i=0; i<g.vexnum; i++) {
if(i!=0 && D[i]!=INFINITY) {
cout<<g.vexs[0]<<"-"<<g.vexs[i]<<"的最短路径长度为:"<<D[i];
cout<<" 最短路径为:";
for(j=0; j<g.vexnum; j++) {
if(p[i][j]>-1)
cout<<g.vexs[p[i][j]]<<" ";
}
cout<<endl;
} else if(D[i]==INFINITY)
cout<<g.vexs[0]<<"-"<<g.vexs[i]<<":"<<"不可达"<<endl;
}
return 0;
}
样例输入
请输入顶点数和边数:5 7
请输入顶点:A B C D E
请输入边和权值:
A D 2
A B 4
B D 1
B C 4
C D 1
D E 7
C E 3
最短路径数组p[i][j]如下:
-1 -1 -1 -1 -1
0 1 -1 -1 -1
0 1 2 -1 -1
0 3 -1 -1 -1
0 3 4 -1 -1
A到各顶点的最短路径及长度为:
A-B的最短路径长度为:4 最短路径为:A B
A-C的最短路径长度为:8 最短路径为:A B C
A-D的最短路径长度为:2 最短路径为:A D
A-E的最短路径长度为:9 最短路径为:A D E
