• 哈夫曼树

    哈夫曼树

    简介

    哈夫曼树（Huffman Tree），又名：最优二叉树，赫夫曼树

    其标准含义是：给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

    相关名词

    由于本篇存在一定的难度，因此在开始相关的学习之前，请让我们来巩固以下本文所涉及的名词知识点。

    a) 路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径。

    b) 路径长度：在一条路径中，每经过一个结点，路径长度都要加 1 。例如在一棵树中，规定根结点所在层数为1层，那么从根结点到第 i 层结点的路径长度为 i - 1 。

    c) 结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权。

    d) 结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。

    e)  树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL”。

    构建哈夫曼树

    在构建哈夫曼树时，只需要遵循一个原则，那就是权重越大的结点距离树根越近。

    因此，在构建过程中，有如下的规律：

    31.png

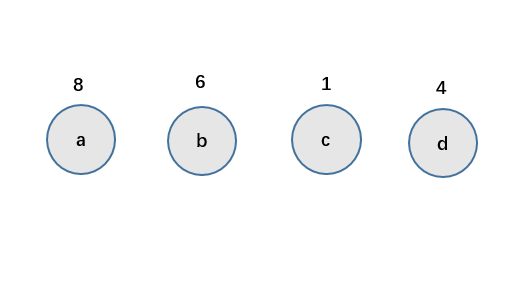
    首先，选出我们数据中最小的两个数据，构建成二叉树的左孩子和右孩子，而根的数据为两者之和

    32.png

    33.png

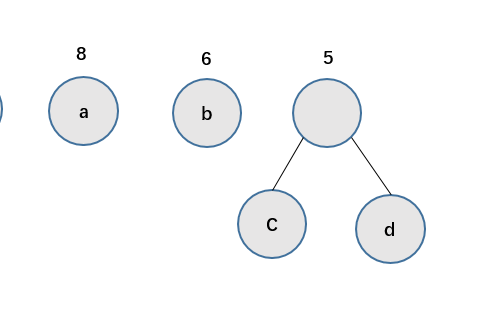
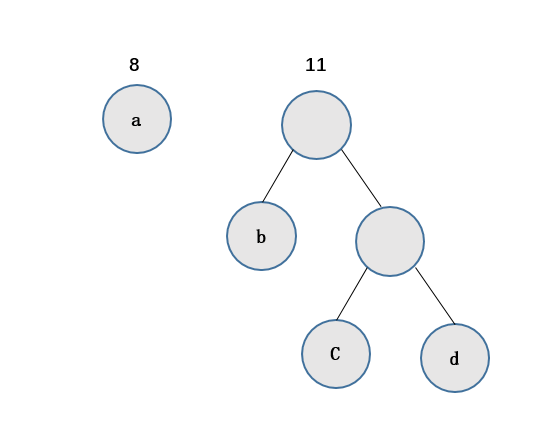
    其次，将刚才合成的数据作为右孩子，左孩子从未处理的数据中选出最小的一个，作为左孩子，他们的根同样为左右孩子的权值和

    34.png

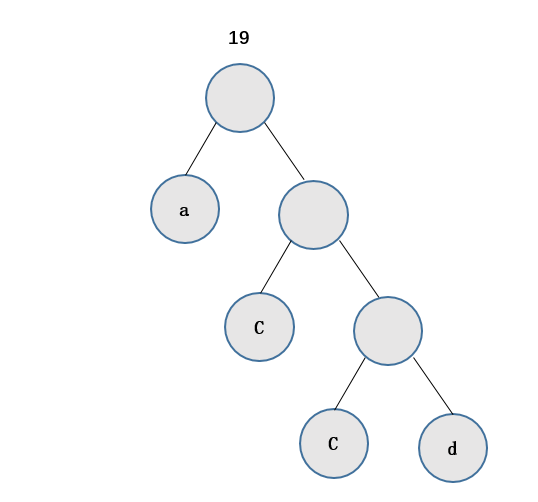
    不断重复上述的步骤，直到将所有的数据全部处理完并构建出二叉树，这棵二叉树就是我们的哈夫曼树。

    如图这颗哈夫曼树的WPL值为：WPL= 8*1+ 6*2 + 1*3 + 4*3 = 273

    哈弗曼树中结点结构

    构建哈夫曼树时，首先需要确定树中结点的构成。由于哈夫曼树的构建是从叶子结点开始，不断地构建新的父结点，直至树根，所以结点中应包含指向父结点的指针。但是在使用哈夫曼树时是从树根开始，根据需求遍历树中的结点，因此每个结点需要有指向其左孩子和右孩子的指针。

    所以，哈夫曼树中结点构成用代码表示为：

    //哈夫曼树结点结构
typedef struct {
    int weight;//结点权重
    int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
}HTNode, *HuffmanTree;

    哈弗曼树中的查找算法

    构建哈夫曼树时，需要每次根据各个结点的权重值，筛选出其中值最小的两个结点，然后构建二叉树。

    查找权重值最小的两个结点的思想是：从树组起始位置开始，首先找到两个无父结点的结点（说明还未使用其构建成树），然后和后续无父结点的结点依次做比较，有两种情况需要考虑：

      • 如果比两个结点中较小的那个还小，就保留这个结点，删除原来较大的结点；
      • 如果介于两个结点权重值之间，替换原来较大的结点；
    //HT数组中存放的哈夫曼树，end表示HT数组中存放结点的最终位置，s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
void Select(HuffmanTree HT, int end, int *s1, int *s2)
{
    int min1, min2;
    //遍历数组初始下标为 1
    int i = 1;
    //找到还没构建树的结点
    while(HT[i].parent != 0 && i <= end){
        i++;
    }
    min1 = HT[i].weight;
    *s1 = i;
   
    i++;
    while(HT[i].parent != 0 && i <= end){
        i++;
    }
    //对找到的两个结点比较大小，min2为大的，min1为小的
    if(HT[i].weight < min1){
        min2 = min1;
        *s2 = *s1;
        min1 = HT[i].weight;
        *s1 = i;
    }else{
        min2 = HT[i].weight;
        *s2 = i;
    }
    //两个结点和后续的所有未构建成树的结点做比较
    for(int j=i+1; j <= end; j++)
    {
        //如果有父结点，直接跳过，进行下一个
        if(HT[j].parent != 0){
            continue;
        }
        //如果比最小的还小，将min2=min1，min1赋值新的结点的下标
        if(HT[j].weight < min1){
            min2 = min1;
            min1 = HT[j].weight;
            *s2 = *s1;
            *s1 = j;
        }
        //如果介于两者之间，min2赋值为新的结点的位置下标
        else if(HT[j].weight >= min1 && HT[j].weight < min2){
            min2 = HT[j].weight;
            *s2 = j;
        }
    }
}

    构建哈弗曼树的代码实现

    //HT为地址传递的存储哈夫曼树的数组，w为存储结点权重值的数组，n为结点个数
void CreateHuffmanTree(HuffmanTree *HT, int *w, int n)
{
    if(n<=1) return; // 如果只有一个编码就相当于0
    int m = 2*n-1; // 哈夫曼树总节点数，n就是叶子结点
    *HT = (HuffmanTree) malloc((m+1) * sizeof(HTNode)); // 0号位置不用
    HuffmanTree p = *HT;
    // 初始化哈夫曼树中的所有结点
    for(int i = 1; i <= n; i++)
    {
        (p+i)->weight = *(w+i-1);
        (p+i)->parent = 0;
        (p+i)->left = 0;
        (p+i)->right = 0;
    }
    //从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
    for(int i = n+1; i <= m; i++)
    {
        (p+i)->weight = 0;
        (p+i)->parent = 0;
        (p+i)->left = 0;
        (p+i)->right = 0;
    }
    //构建哈夫曼树
    for(int i = n+1; i <= m; i++)
    {
        int s1, s2;
        Select(*HT, i-1, &s1, &s2);
        (*HT)[s1].parent = (*HT)[s2].parent = i;
        (*HT)[i].left = s1;
        (*HT)[i].right = s2;
        (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
    }
}

    哈夫曼编码

    哈夫曼编码就是在哈夫曼树的基础上构建的，这种编码方式最大的优点就是用最少的字符包含最多的信息内容。

    根据发送信息的内容，通过统计文本中相同字符的个数作为每个字符的权值，建立哈夫曼树。对于树中的每一个子树，统一规定其左孩子标记为 0 ，右孩子标记为 1 。这样，用到哪个字符时，从哈夫曼树的根结点开始，依次写出经过结点的标记，最终得到的就是该结点的哈夫曼编码。

    文本中字符出现的次数越多，在哈夫曼树中的体现就是越接近树根。编码的长度越短。

     


    　　图 3 哈夫曼编码

    如图 3 所示，字符 a 用到的次数最多，其次是字符 b 。字符 a 在哈夫曼编码是 0 ，字符 b 编码为 10 ，字符 c 的编码为 110 ，字符 d 的编码为 111 。

    使用程序求哈夫曼编码有两种方法：

    1. 从叶子结点一直找到根结点，逆向记录途中经过的标记。例如，图 3 中字符 c 的哈夫曼编码从结点 c 开始一直找到根结点，结果为：0 1 1 ，所以字符 c 的哈夫曼编码为：1 1 0（逆序输出）。
    2. 从根结点出发，一直到叶子结点，记录途中经过的标记。例如，求图 3 中字符 c 的哈夫曼编码，就从根结点开始，依次为：1 1 0。


    采用方法 1 的实现代码为：

    //HT为哈夫曼树，HC为存储结点哈夫曼编码的二维动态数组，n为结点的个数
void HuffmanCoding(HuffmanTree HT, HuffmanCode *HC,int n){
    *HC = (HuffmanCode) malloc((n+1) * sizeof(char *));
    char *cd = (char *)malloc(n*sizeof(char)); //存放结点哈夫曼编码的字符串数组
    cd[n-1] = '';//字符串结束符
   
    for(int i=1; i<=n; i++){
        //从叶子结点出发，得到的哈夫曼编码是逆序的，需要在字符串数组中逆序存放
        int start = n-1;
        //当前结点在数组中的位置
        int c = i;
        //当前结点的父结点在数组中的位置
        int j = HT[i].parent;
        // 一直寻找到根结点
        while(j != 0){
            // 如果该结点是父结点的左孩子则对应路径编码为0，否则为右孩子编码为1
            if(HT[j].left == c)
                cd[--start] = '0';
            else
                cd[--start] = '1';
            //以父结点为孩子结点，继续朝树根的方向遍历
            c = j;
            j = HT[j].parent;
        }
        //跳出循环后，cd数组中从下标 start 开始，存放的就是该结点的哈夫曼编码
        (*HC)[i] = (char *)malloc((n-start)*sizeof(char));
        strcpy((*HC)[i], &cd[start]);
    }
    //使用malloc申请的cd动态数组需要手动释放
    free(cd);
}

    采用第二种算法的实现代码为：

    //HT为哈夫曼树，HC为存储结点哈夫曼编码的二维动态数组，n为结点的个数
void HuffmanCoding(HuffmanTree HT, HuffmanCode *HC,int n){
    *HC = (HuffmanCode) malloc((n+1) * sizeof(char *));
    int m=2*n-1;
    int p=m;
    int cdlen=0;
    char *cd = (char *)malloc(n*sizeof(char));
    //将各个结点的权重用于记录访问结点的次数，首先初始化为0
    for (int i=1; i<=m; i++) {
        HT[i].weight=0;
    }
    //一开始 p 初始化为 m，也就是从树根开始。一直到p为0
    while (p) {
        //如果当前结点一次没有访问，进入这个if语句
        if (HT[p].weight==0) {
            HT[p].weight=1;//重置访问次数为1
            //如果有左孩子，则访问左孩子，并且存储走过的标记为0
            if (HT[p].left!=0) {
                p=HT[p].left;
                cd[cdlen++]='0';
            }
            //当前结点没有左孩子，也没有右孩子，说明为叶子结点，直接记录哈夫曼编码
            else if(HT[p].right==0){
                (*HC)[p]=(char*)malloc((cdlen+1)*sizeof(char));
                cd[cdlen]='';
                strcpy((*HC)[p], cd);
            }
        }
        //如果weight为1，说明访问过一次，即是从其左孩子返回的
        else if(HT[p].weight==1){
            HT[p].weight=2;//设置访问次数为2
            //如果有右孩子，遍历右孩子，记录标记值 1
            if (HT[p].right!=0) {
                p=HT[p].right;
                cd[cdlen++]='1';
            }
        }
        //如果访问次数为 2，说明左右孩子都遍历完了，返回父结点
        else{
            HT[p].weight=0;
            p=HT[p].parent;
            --cdlen;
        }
    }
}

    完整代码

    #include<stdlib.h>
#include<stdio.h>
#include<string.h>
//哈夫曼树结点结构
typedef struct {
    int weight;//结点权重
    int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
}HTNode, *HuffmanTree;
//动态二维数组，存储哈夫曼编码
typedef char ** HuffmanCode;
//HT数组中存放的哈夫曼树，end表示HT数组中存放结点的最终位置，s1和s2传递的是HT数组中权重值最小的两个结点在数组中的位置
void Select(HuffmanTree HT, int end, int *s1, int *s2)
{
    int min1, min2;
    //遍历数组初始下标为 1
    int i = 1;
    //找到还没构建树的结点
    while(HT[i].parent != 0 && i <= end){
        i++;
    }
    min1 = HT[i].weight;
    *s1 = i;
   
    i++;
    while(HT[i].parent != 0 && i <= end){
        i++;
    }
    //对找到的两个结点比较大小，min2为大的，min1为小的
    if(HT[i].weight < min1){
        min2 = min1;
        *s2 = *s1;
        min1 = HT[i].weight;
        *s1 = i;
    }else{
        min2 = HT[i].weight;
        *s2 = i;
    }
    //两个结点和后续的所有未构建成树的结点做比较
    for(int j=i+1; j <= end; j++)
    {
        //如果有父结点，直接跳过，进行下一个
        if(HT[j].parent != 0){
            continue;
        }
        //如果比最小的还小，将min2=min1，min1赋值新的结点的下标
        if(HT[j].weight < min1){
            min2 = min1;
            min1 = HT[j].weight;
            *s2 = *s1;
            *s1 = j;
        }
        //如果介于两者之间，min2赋值为新的结点的位置下标
        else if(HT[j].weight >= min1 && HT[j].weight < min2){
            min2 = HT[j].weight;
            *s2 = j;
        }
    }
}
//HT为地址传递的存储哈夫曼树的数组，w为存储结点权重值的数组，n为结点个数
void CreateHuffmanTree(HuffmanTree *HT, int *w, int n)
{
    if(n<=1) return; // 如果只有一个编码就相当于0
    int m = 2*n-1; // 哈夫曼树总节点数，n就是叶子结点
    *HT = (HuffmanTree) malloc((m+1) * sizeof(HTNode)); // 0号位置不用
    HuffmanTree p = *HT;
    // 初始化哈夫曼树中的所有结点
    for(int i = 1; i <= n; i++)
    {
        (p+i)->weight = *(w+i-1);
        (p+i)->parent = 0;
        (p+i)->left = 0;
        (p+i)->right = 0;
    }
    //从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点
    for(int i = n+1; i <= m; i++)
    {
        (p+i)->weight = 0;
        (p+i)->parent = 0;
        (p+i)->left = 0;
        (p+i)->right = 0;
    }
    //构建哈夫曼树
    for(int i = n+1; i <= m; i++)
    {
        int s1, s2;
        Select(*HT, i-1, &s1, &s2);
        (*HT)[s1].parent = (*HT)[s2].parent = i;
        (*HT)[i].left = s1;
        (*HT)[i].right = s2;
        (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;
    }
}
//HT为哈夫曼树，HC为存储结点哈夫曼编码的二维动态数组，n为结点的个数
void HuffmanCoding(HuffmanTree HT, HuffmanCode *HC,int n){
    *HC = (HuffmanCode) malloc((n+1) * sizeof(char *));
    char *cd = (char *)malloc(n*sizeof(char)); //存放结点哈夫曼编码的字符串数组
    cd[n-1] = '';//字符串结束符
   
    for(int i=1; i<=n; i++){
        //从叶子结点出发，得到的哈夫曼编码是逆序的，需要在字符串数组中逆序存放
        int start = n-1;
        //当前结点在数组中的位置
        int c = i;
        //当前结点的父结点在数组中的位置
        int j = HT[i].parent;
        // 一直寻找到根结点
        while(j != 0){
            // 如果该结点是父结点的左孩子则对应路径编码为0，否则为右孩子编码为1
            if(HT[j].left == c)
                cd[--start] = '0';
            else
                cd[--start] = '1';
            //以父结点为孩子结点，继续朝树根的方向遍历
            c = j;
            j = HT[j].parent;
        }
        //跳出循环后，cd数组中从下标 start 开始，存放的就是该结点的哈夫曼编码
        (*HC)[i] = (char *)malloc((n-start)*sizeof(char));
        strcpy((*HC)[i], &cd[start]);
    }
    //使用malloc申请的cd动态数组需要手动释放
    free(cd);
}
//打印哈夫曼编码的函数
void PrintHuffmanCode(HuffmanCode htable,int *w,int n)
{
    printf("Huffman code : 
");
    for(int i = 1; i <= n; i++)
        printf("%d code = %s
",w[i-1], htable[i]);
}
int main(void)
{
    int w[5] = {2, 8, 7, 6, 5};
    int n = 5;
    HuffmanTree htree;
    HuffmanCode htable;
    CreateHuffmanTree(&htree, w, n);
    HuffmanCoding(htree, &htable, n);
    PrintHuffmanCode(htable,w, n);
    return 0;
}
    View Code

     

    总结


    图 4 程序运行效果图


    本节的程序中对权重值分别为 2，8，7，6，5 的结点构建的哈夫曼树如图 4（A）所示。图 4（B）是另一个哈夫曼树，两棵树的带权路径长度相同。

    程序运行效果图之所以是（A）而不是（B），原因是在构建哈夫曼树时，结点 2 和结点 5 构建的新的结点 7 存储在动态树组的最后面，所以，在程序继续选择两个权值最小的结点时，直接选择了的叶子结点 6 和 7 。

    因上求缘，果上努力~~~~ 作者：每天卷学习，转载请注明原文链接：https://www.cnblogs.com/BlairGrowing/p/13667642.html
  • 相关阅读:
    前端代码美化的艺术
    CSS3 简单的砸金蛋样式
    为什么 VS Code 能迅速占领 JavaScript 开发者社区
    了解并使用 CSS 中的 rem 单位
    CSS中一些利用伪类、伪元素和相邻元素选择器的技巧
    SVG入门指南
    PAT 1035 Password [字符串][简单]
    生信学习-二代测序知乎专栏总结[转]
    PAT 1119 Pre- and Post-order Traversals [二叉树遍历][难]
    生信笔记-mooc【武大】
  • 原文地址：https://www.cnblogs.com/BlairGrowing/p/13667642.html
Copyright © 2020-2023  润新知