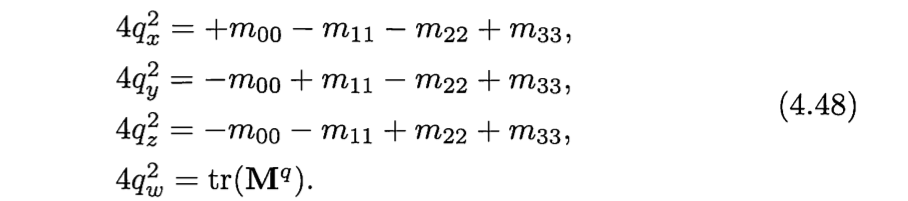四元数产生于1843年,是复数的一个扩展,所以里面包含了一些复数的运算。直到1985年才在图形学中使用。
四元数的优势是,相对与矩阵和欧拉角,四元数更直观和方便。四元数还可以用作某些方向上的插值,而欧拉角可能并不能很好的完成。
四元数使用四个数字表示。通常,前三个和旋转的轴密切相关,最后一个和旋转的角度相关。以下是一些数学背景,对于后面的四元数的变化十分重要。
注意到四元数是复数的一个扩展,那么可以表示为:Û = (â, v), 其中 v 是一个实数,而 â 则是可以看成是虚部,且 â= i*qx + j*qy + k*qz 其中,i j k 都是虚部,他们的计算为
i2 = j2= k2 = -1 , jk = -kj=i , ik = -ki = j , ij = -ji = k ,因为â 含有三个部分,所以,一些向量的操作也是可以用在四元数的虚部上。
对于两个四元数相乘,如下图:
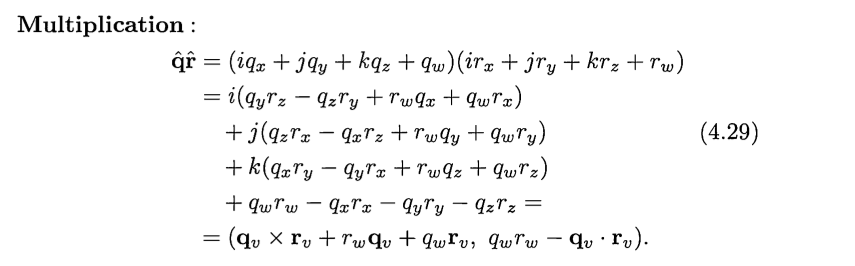
关于其他计算如下:
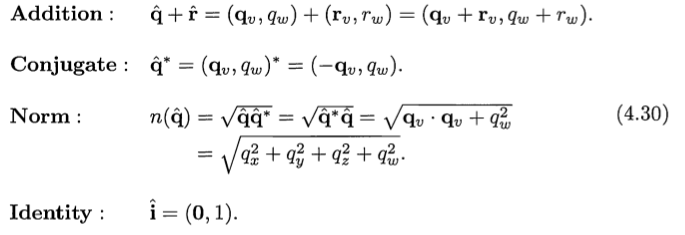
其中 conjugate 是共轭的意思。根据norm运算我们可以推出除法运算:
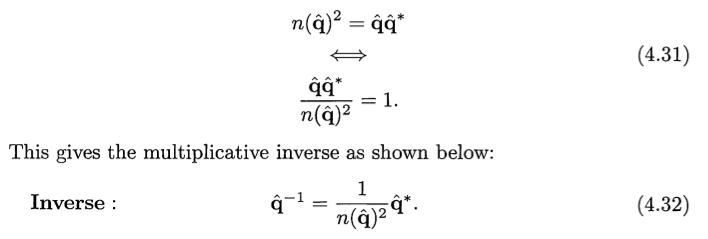
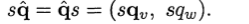
以及其他一些运算规则:

对于单位四元数,我们还可以用下面的方法进表示,这也是表达旋转变化比较直观的方式
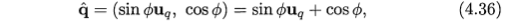
其计算过程如下,其中要求uq是单位向量:
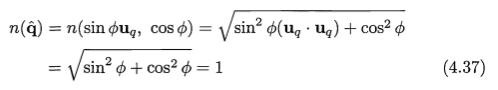
另一种表达方式如下,其可以解决log和平方运算:


对于单位四元数的直观理解如下图:

以上是四元数的基本知识背景。下面来介绍四元数表示的变化。
我们只使用四元数中的一个子集,单位四元数来进行各种旋转变化,十分简单和强大。变化方程为:

其q是一个单位四元数,其形式为公式4.36,而p则是一个四次其次的点或者向量,p的每个部分直接代替四元数的各个部分,形成一个新的四元数。注意到q是单位四元数,所以q-1 = q*。而且,单位四元数与实数相乘并不能改变四元数的作用效果,所以四元数q 和-q的作用效果一样的。那么在从矩阵转化到四元数的过程中,可能得到q也可能得到-q。公式4.40的直观理解就是上面的图。下面的公式代表两个四元数数对一个p进行变化。

四元数和矩阵的转化。因为在硬件上使用矩阵要比使用四元数计算的更快,所以可以在应用层面上使用四元数,但是在计算层面上使用矩阵。他们之间的转化为:
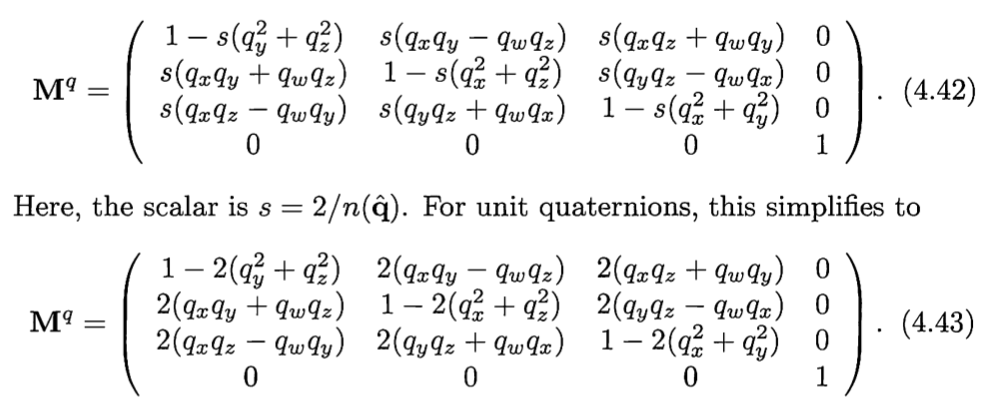
但是在应用层面上要使用四元数时,又要从矩阵转化成四元数。通过观察,可以看到以下等式
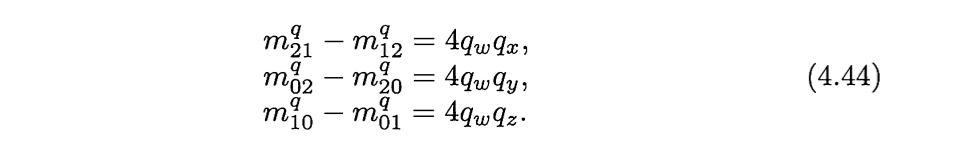
如果直到qw , qx , qy , qz中的任何一个,都可以计算出另外三个。通过观察可以知道如下等式:
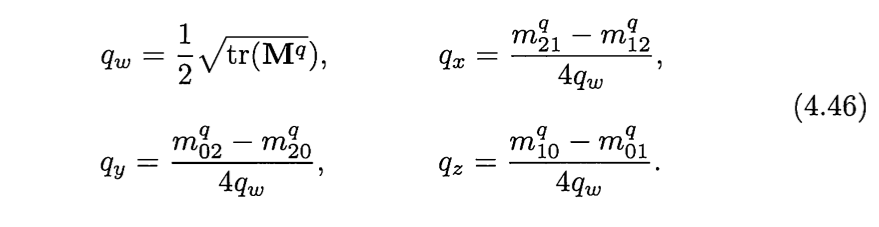
其中tr(Mq)的意思时矩阵的迹,也就是矩阵对角线的和。在计算过程中,我们知道应该尽量避免除以一个比较小的数字。所以4.46不一定时最好的算法。通过以下比较
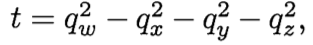
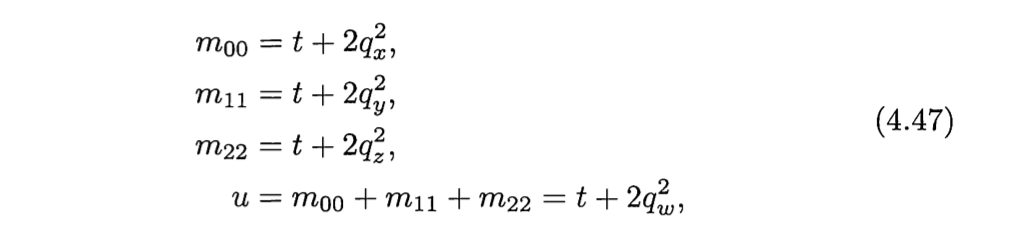
可知,通过比较矩阵的几个元素和u的大小就可以知道qx qy qz qw 的大小关系。如果qw 最大,那么直接使用4.46就可以。如果不是,那么可以使用如下方法,算出最大的那个元素值,然后决定使用4.44时那个元素作为分母。