一、大O记号(表示上界)
1. f(n) = O(g(n))
意味着:存在常数 C>0,n0>0,使得任意 n≥n0,有 0 ≤ f(n) ≤ C·g(n) 成立。
如:2n2 = O(n3) 。
2. 可以将大O理解为一个函数集:
O(g(n)) = { f(n) | 存在常数 C>0,n0>0,使得任意 n≥n0,有 0 ≤ f(n) ≤ C·g(n) 成立 }
O(g(n)) = { f(n) | 存在常数 C>0,n0>0,使得任意 n≥n0,有 0 ≤ f(n) ≤ C·g(n) 成立 }
因此,等号并不对称,严格来说是“属于集合符号”:∈ 。
3. 误差界限:
例:f(n) = n3 + O(n2),即 f(n) 主要是 n3,但也有一些低阶项 O(n2) 。
例:f(n) = n3 + O(n2),即 f(n) 主要是 n3,但也有一些低阶项 O(n2) 。
即:存在函数 f(n),有 h(n)∈O(n2) 使得 f(n) = n3 + h(n)。
首先描述的是首项 n3,然后加上至多为 n2 的误差项。
4. 更微妙的等式:
例:n2 + O(n) = O(n3),也是等号不对称。
例:n2 + O(n) = O(n3),也是等号不对称。
等号不表示“等于”,而表示“是”,即所有等号左边的都是等号右边的。
即:存在 O(n3),有任意 n2 + O(n) 都是 O(n3);反之则不然,所以不对称。
准确定义:对于任意 f(n)∈O(n),存在 h(n)∈O(n3),使得 n2 + f(n) = h(n) 成立。
5. 等式关系链:等式可以从左到右传递下去,即可理解为是通过“什么是什么”组成的链式表达式,
第一个就是最后一个,或者说以最后一个为上界。但不能反过来从后往前传递。
第一个就是最后一个,或者说以最后一个为上界。但不能反过来从后往前传递。
二、大Ω符号(表示下界)
1. f(n) = Ω(g(n))
Ω(g(n)) = { f(n) | 存在常数 C>0,n0>0,使得任意 n≥n0,有 0 ≤ C·g(n) ≤ f(n) 成立 }
1. f(n) = Ω(g(n))
Ω(g(n)) = { f(n) | 存在常数 C>0,n0>0,使得任意 n≥n0,有 0 ≤ C·g(n) ≤ f(n) 成立 }
2. 例:√n = Ω(lgn),即对于足够大的 n,√n 至少是 Ω(lgn) 的常数倍。
三、大Θ符号
三、大Θ符号
1. Θ(n) = O(n) ∩ Ω(n)
2. Θ(g(n)) = { f(n) | 存在常数 C1>0,C2>0,n0>0,使得任意 n≥n0,有 0 ≤ C1·g(n) ≤ f(n) ≤ C2·g(n) }
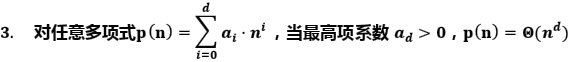
四、小o符号和小ω符号
1. o(g(n)) = { f(n) | 任意常数 C>0,存在 n0>0,使得任意 n≥n0,有 0 ≤ f(n) < C·g(n) 成立 }
lim [ f(n) / g(n) ] = 0 as n->∞
2. ω(g(n)) = { f(n) | 任意常数 C>0,存在 n0>0,使得任意 n≥n0,有 0 ≤ C·g(n) < f(n) 成立 }
lim [ f(n) / g(n) ] = ∞ as n->∞
3. 例:2n2 = o(n3),
证:存在 n0>0,当 n>n0,有 2n2 < C·n3,即 n > 2/C
取 n = [n0],则 n0 = 2/C 。
即存在 n0 = 2/C ,当 n>n0,有 2n2 < C·n3 成立,即 2n2 = o(n3) 。
4. 注:1/2n2 = Θ(n2) ≠ o(n2)
≠ ω(n2)
五、性质及类比:
1. 传递性:
f(n) = Ө(g(n)) 和 g(n) = Ө(h(n)) => f(n) = Ө(h(n))
f(n) = O(g(n)) 和 g(n) = O(h(n)) => f(n) = O(h(n))
f(n) = Ω(g(n)) 和 g(n) = Ω(h(n)) => f(n) = Ω(h(n))
f(n) = o(g(n)) 和 g(n) = o(h(n)) => f(n) = o(h(n))
f(n) = ω(g(n)) 和 g(n) = ω(h(n)) => f(n) = ω(h(n))
2. 自反性:
f(n) = Ө(f(n))
f(n) = O(f(n))
f(n) = Ω(f(n))
3. 转置对称性:
f(n) = Ө(g(n)) 当且仅当 g(n) = Ө(f(n))
f(n) = O(g(n)) 当且仅当 g(n) = Ω(f(n))
f(n) = o(g(n)) 当且仅当 g(n) = ω(f(n))
4. 类比:
可以类比:O Ω Θ o ω
≤ ≥ = < >
但类比并不是等价于;同时小符号是大符号更为严格的记号,但却没有严格的小θ。