前言
本文会全面的介绍java中的移动运算符,虽从基础开始,但是最好先了解什么是二进制,以及十进制如何转换成二进制这些基本知识后再进行阅读。另外本文中会使用下标的方式表示一个数的进制,如下:
(10)10 :表示10进制的10
(10)2 :表示2进制的10,它和(2)10数值相等
一、原码,反码,补码
1、二进制运算
在java中,有八种基本数据类型。其中整数类型有四种,分别是byte、short、int、long。这几种数据类型各自都有自己的长度限制。比如byte是8位,int是32位等。这里所说的"位数"指的就是换算成二进制后所占的位数。毕竟在计算机中都是使用二进制的方式进行运算的。为了方便起见,在本节的例子中,二进制数都会以8位为例。
由于计算机的运算是使用二进制进行,所以首先第一步肯定是将我们常用的十进制数转换成二进制数,然后进行运算,运算结束之后再将二进制转回十进制形成最终结果给人看。
比如:(1)10 + (10)10 = (11)10
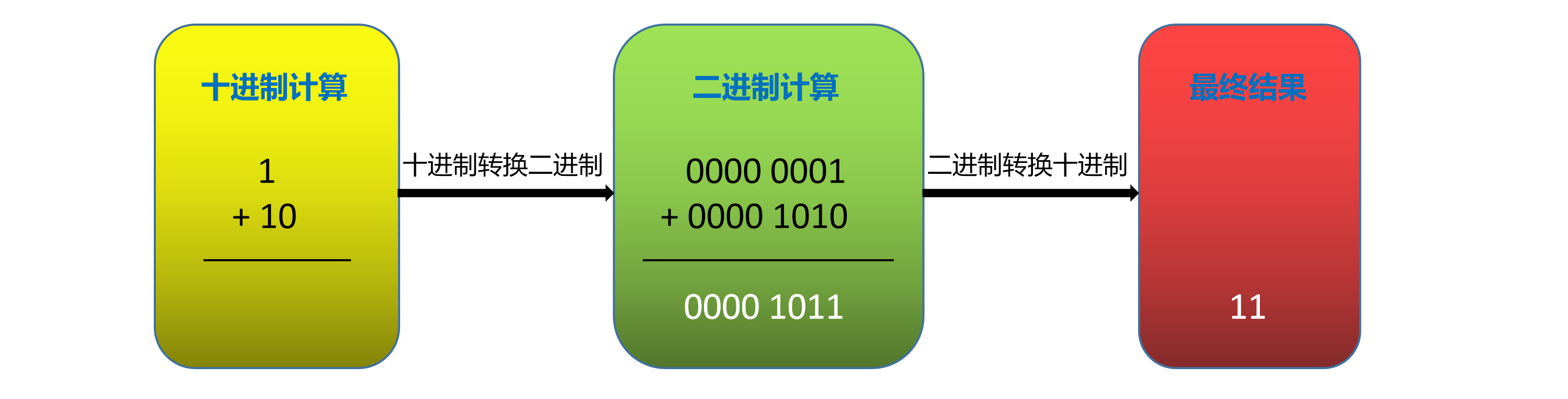
上面是两个正数转换成二进制之后求和。如果有一定的进制转换知识的话,这个运算理解起来应该是非常简单的。不过如果运算的数字中除了正数,还有负数。比如(-1)10又该如何运算呢?
为了区分正负,人为规定取最高位(左起第1位)为符号位。同时规定符号位为0表示该数为正,1表示该数为负,剩下的位数表示数值。比如(1)10转换成二进制就是(0000 0001)2,那(-1)10转换成二进制自然就是(1000 0001)2了。下面再举两个例子:
(10)10 = (0000 1010)2
(-10)10 = (1000 1010)2
可以看到这个规定理解起来没有任何难度,但是如果使用这种二进制进行计算,在负数的情形下,是无法得到正确的结果的。情形如下所示:
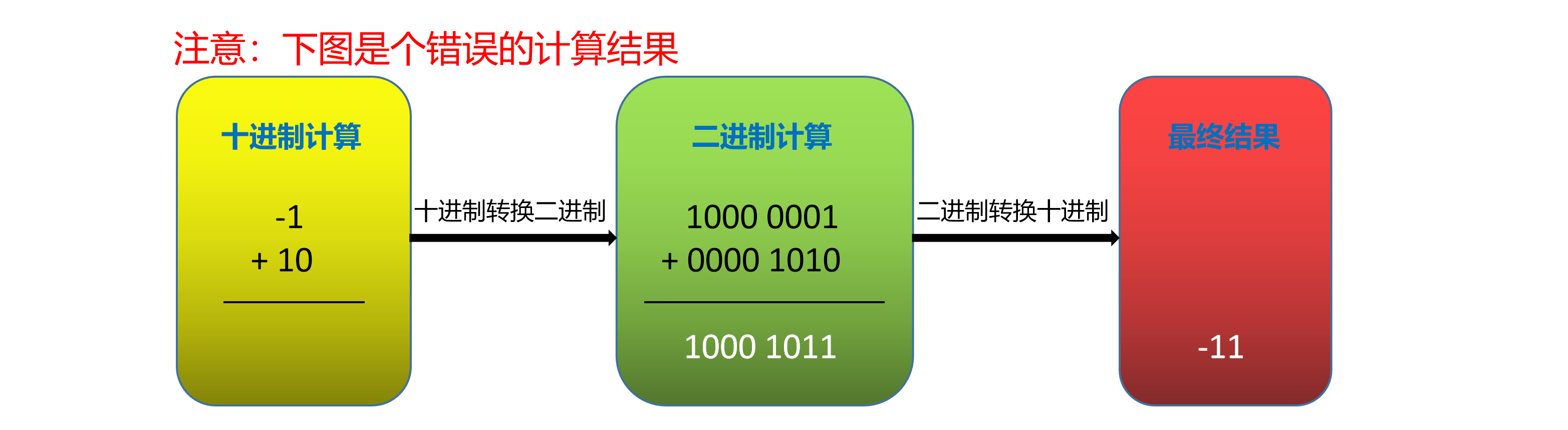
很明显,上面的计算在十进制转化成二进制时是遵循以上规则的,但是计算结果却明显有问题,这说明这样直接计算是不对的。这个问题其实出在负数上。
实际在计算机中,所有的运算都必须使用补码进行运算。上面得到的二进制数实际上都是所谓的原码,关于原码和补码的关系如下表所示:
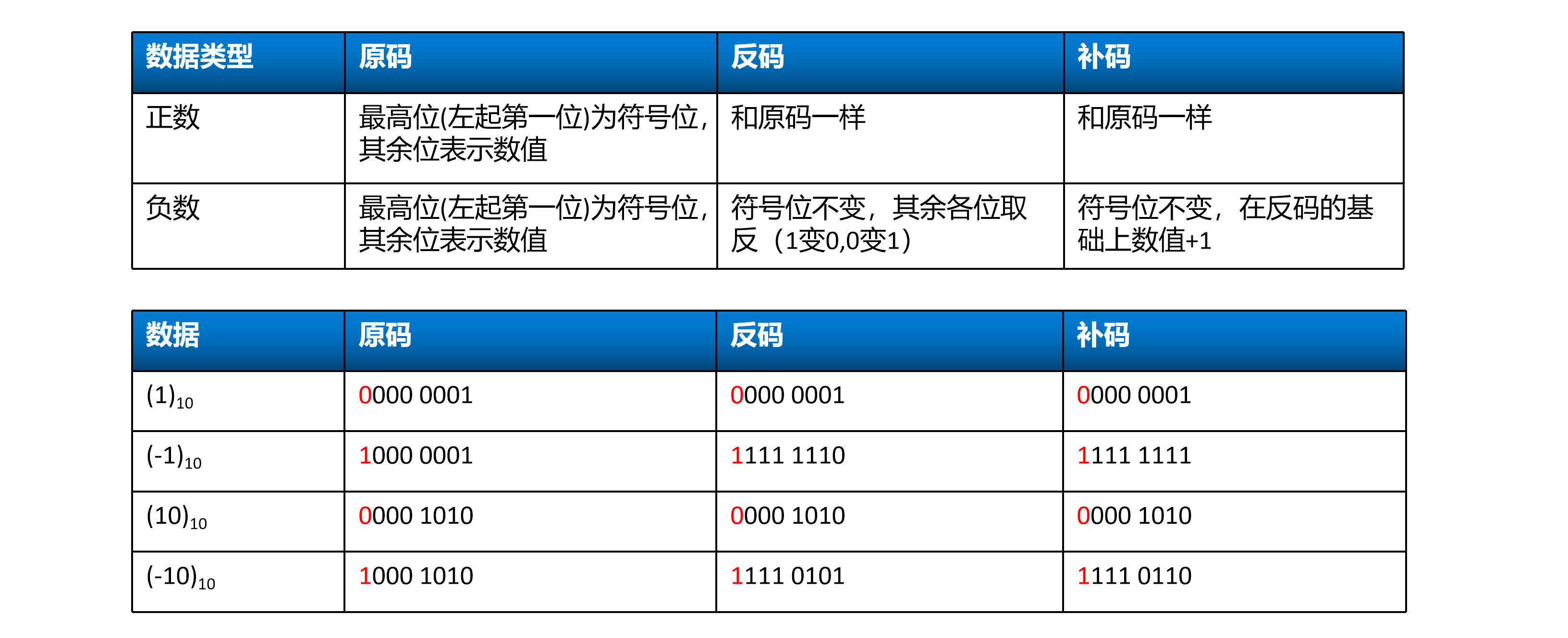
可以看到,正数由于"三码"一致,处理起来比较简单;相对而言对负数就要麻烦一些,处理起来也要小心些。了解了补码后,会发现之前的(-1)10在转成二进制后使用的是原码,需进行修改。使用补码再重新计算一次,情况如下所示:
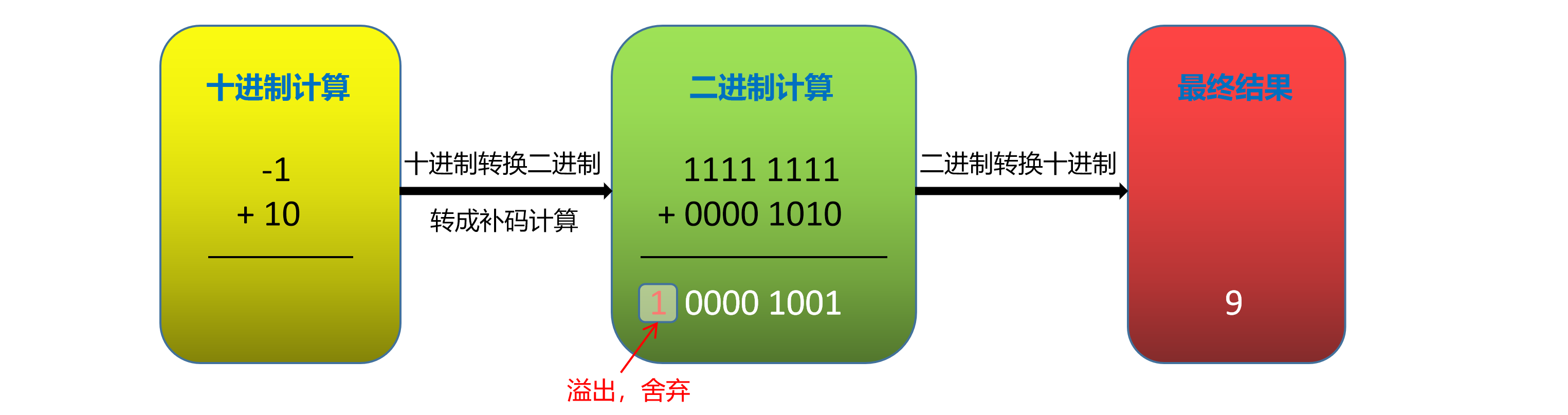
需要说明的是,在二进制计算中,(1111 1111)2和(0000 1010)2相加,总位数明显超过了8位,此时多出的位数会被自动舍弃,仅保留有效的8位。该性质在二进制计算中被广泛使用,有时也会因此产生意想不到的bug。当然在这里是没有bug的。
可以看到,这次运算得到了正确的结果。这说明所有的二进制运算都必须使用补码进行。无论正数还是负数,都需要先转换成补码,再进行运算。正数无需特意转换仅仅是因为它的原、反、补一致而已。
2、二进制数运算步骤
从上面的例子中,可以得到一般情况下二进制运算的步骤:
① 将需要进行运算的数据转换成相应的二进制补码形式;
② 进行相应的运算,溢出位舍弃,这里得到的结果仍然是补码(补码之间运算的到的仍是补码);
③ 将计算得到的结果转换回原码。如果最高位是0表示结果是正数,无需处理。如果最高位为1,那么需进行转换。补码转成原码和上面的原码转补码是互为逆运算。
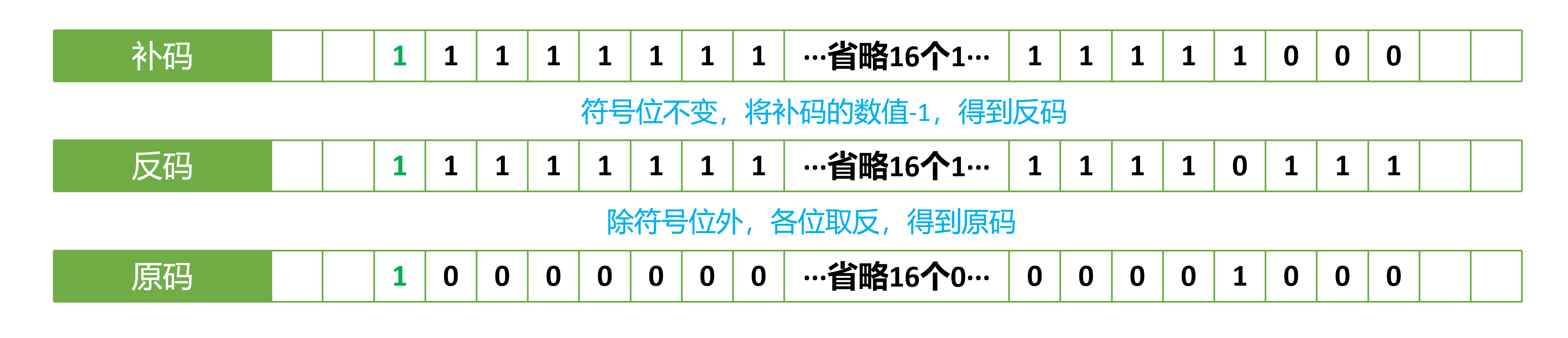
补码转原码:1 - 符号位不变,将补码的数值-1,得到反码;
2 - 除符号位外,各位取反,得到原码;
3、关于补码的理解
如果只是按照上述规则来计算,其实并不难,毕竟规则还是比较简单好记的。但是补码这个东西确实让人觉得有一丝丝的不快。(10)10 = (0000 1010)2这个转换很好理解,(-10)10 = (1000 1010)2这个转换也还行,但是却不能用来计算,这就有点难受了,而且必须要转换成补码才能得到正确的结果。死记硬背当然没问题,但是总感觉这个地方转换的太生硬,莫名其妙搞了个补码出来。学到这里感觉像吃了屎一样的难受。
后来在一篇文章上,得到了启发。多年的便秘终于治好了。
对于计算机来说,其实无法区分正数还是负数,它只认数值。即使我们人为规定了符号位,但那只是一厢情愿,并不代表计算机会认。对于正数来说,符号位其实也没有意义。有无符号位对其几乎无影响,因为它的值和它的绝对值一致。那么我们可以认为(10)10 = (0000 1010)2这个等式是没问题的,因为就算不考虑符号,它也是成立的。对于所有的正数来说,同理。这也是为什么正数的正、反、补一致的原因。那么剩下的工作就是要找寻负数的表示方式。
负数在数学上有个性质:一个负数,如果与其绝对值相等的正数相加,那么和一定为0。另外在计算机中,如果两个8位数相加,最终结果得到的是一个9位数,那么其实只有后8位是有效的,最高位会被舍弃,这个性质也叫"高位溢出",在之前的运算中也已经有所体现。根据这两个性质,我们就能找到所有负数的表达方式了。
比如(10)10 = (0000 1010)2这是已知条件,如果找到了一个数"x"和其相加结果为0,那么这个"x"实际上就是(-10)10的二进制表示。根据高位溢出的原则,实际上只要等式"x + (0000 1010)2 = (1 0000 0000)2"成立即可。因为(1 0000 0000)2在8位的情况下,最高位的"1"已经溢出无效了,就相当于(0000 0000)2。此时"x"的值就显而易见了,x = (1111 0110)2。这个值就是(-10)10的二进制表示。
这个理论很通顺,先得到一个正数,如果需要负数的话只需要找一个和其相加为0的数"x"即可,这个"x"就是相对应的负数。这样正数负数就都有了。
但是这里得到的负数的二进制表示和之前介绍的负数的二进制表示(人为规定正负号的那种)似乎不一样,下面我们来进行下对比:
之前的:(-10)10=(1000 1010)2(反码:(1111 0101),补码:(1111 0110)2)
现在的:(-10)10=(1111 0110)2
现在推出的这个二进制表示和之前的原码虽然不一样,但是恰好和之前介绍的补码一致。
到此,其实结论就已经呼之欲出了。计算机中的二进制表示实际上就应该是补码,而且只有用它计算才能得到正确结果。正数可以直接表示,负数可以由相应的正数得到。理论上是不需要原码和反码的。但是正常人类无法方便的根据一个负数直接得到其补码形式,为了人们的理解和计算更加方便,才整出了原码和反码的概念。客观上说原码和反码只是人类再试图更好的理解计算机语言——补码时的附属品而已。
二、移位运算符
1、小试牛刀
有了上面的基础,下面开始正式介绍移位运算符。
移位运算也是一种运算。这里的"位"和byte长度限定8位中的"位"含义一致,都是针对二进制的。将二进制数向某个方向整体移动指定位数,就是移位运算。
这里先举一个简单的例子,方便理解。以2 << 1 为例,计算步骤如下:
① 先将2变为补码(所有运算必须以补码形式运行),(2)10 = (0000······0010)2;
② 将上述数值按指定方向移动1位,后面补0,移动之后得到 (0000······0100)2;
③ 将结果转回原码展示出来(正数无需处理,负数需要转换), (0000······0100)2 = (4)10;
其中移位的过程如下图所示:
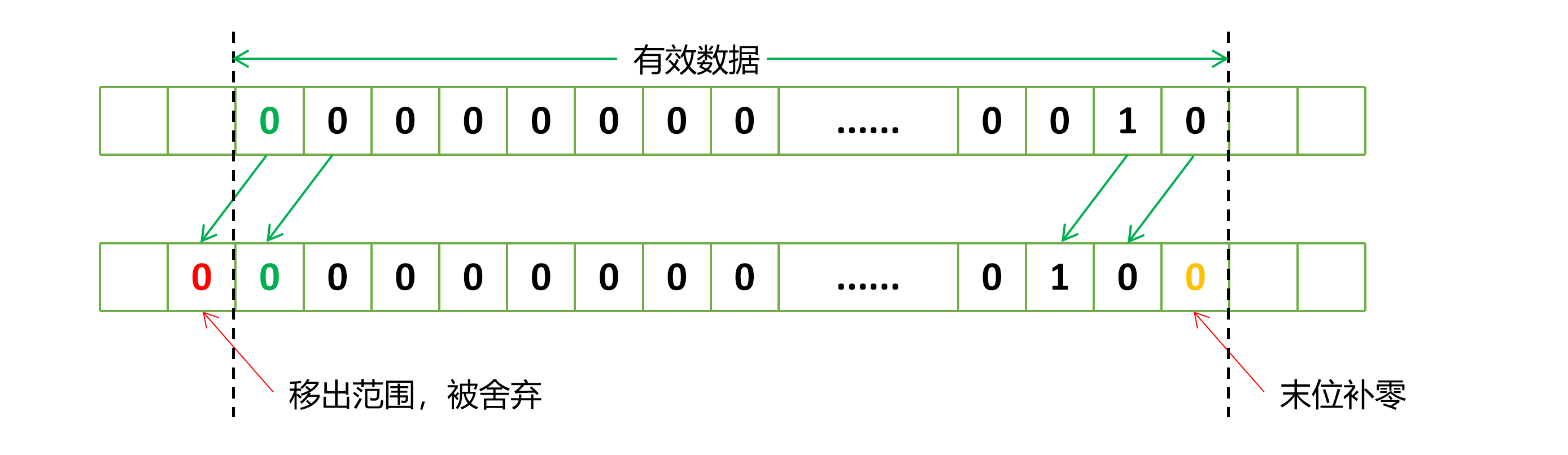
根据运算的情况,可以得出下列等式: 2 << 1 = 4 。单从这个结果来看,向左移动1位,相当于将数值扩大了一倍。从图上也可以很好的理解这一点。二进制上的1被从右起第二位移动到了右起第三位,由于是二进制,所以数值就x2了。如果是十进制的话,向上移动一位,就是x10。
这也是通常说的,左移一位相当于x2。表面上看是这样的,但是这个说法实际上是错误的。同样的还有一个说法,右移(>>)一位相当于÷2,这个说法同样是错误的。
单就上面这个运算的过程和结果来说,毫无疑问是正确的,错误的地方在于移位运算的规则没有上述的这么简单,上述情形只能算作是移位运算下的一个特例。下面就开始真正的认识移位运算。
2、真正的移位运算
移位运算算是java中的"底层陷阱"之一。稍不注意就会出现意想不到的结果。比如1 << 33 = 2 这种,就让人感觉很奇怪;还有更加神奇的,1 << -2 = 1073741824 ,按照之前的那种移位思路,完全无法想象是怎样得到的这种结果。
关于移位运算的情况,在《Java解惑》一书的"谜题27:变幻莫测的i值"中和《Java编程思想》"3.11 移位操作符"中均有介绍,这两处都向我们展示了java中使用移位运算的正确姿势。
在java中移位运算总共分为三种,情况如下图所示:

这三种运算整体形式都是一致的,都是"左操作数 + 运算符 + 右操作数",本文将这种运算表示成如下形式:
value 运算符 num
比如 "2 >> 1",此时表示 value = 2,num = 1。在本文中都会以value代指左操作数,num代指右操作数。
在移位运算中有些通用的规则,这些规则针对三种移位运算都是有效的,规则如下:
① 在java的移位运算中value取值只能是五种基本数据类型,分别是char、byte、short、int、long。其中char是可以被转换成整型的,所以说value的取值范围可以认为只能是整型。比如后面这个式子就会报语法错误:1f >> 1 ;
② 实际上value的取值只有两种类型,分别是int和long。当代码中value的值是byte、short、char类型的时候,在运算前会被先转换成相应的int类型,然后再进行移位运算。比如((byte)1) << 8 ,在该运算中左操作数实际是int类型的1。
③ 由于value的实际取值只有int和long两种类型,这两种类型所占据的位数是有限的,所以就衍生出了第三条规则。运算前应先将num转换成补码形式,当value是int类型时,num只有右侧的低五位有效;当value是long类型时,num只有右侧低六位有效。这个运算规则也是移位运算会出现许多意想不到的情况的罪魁祸首,所以有必要针对该规则做下详细的说明。
3、规则③的说明
在最开始,已阐述了计算机中必须使用补码进行计算的必要性,这里还要在强调的原因是不仅是value要遵循该规则,num在使用时一样需遵循该规则,也就是num也必须转成补码之后才能进行使用。
可以说,在计算机中,只要涉及二进制操作,都必须使用补码进行。
当value值是int类型时,长度为32位。如果移动位数是32位(或32位以上)的话,那么结果将会和移位之前的value没有任何关系,因为所有的位数都消失了。所以java的开发者认为这种操作是无意义的。因此当value是int类型时,num的实际大小被限制在了低五位(二进制补码的低五位)上,这样最大也只会移动31位,不会达到32位。
同样,如果value是long类型的话,那么num的实际大小被限制在了低六位(二进制补码的低六位)上,因为long类型的最大长度为64,最多只能移动63位。
下面准备开始根据上面的规则来进行实际操作,以带符号左移开头,展示移位操作一般情况下的正确姿势。
4、带符号左移(<<)
在本节示例中,例子①会展示移位的过程和计算移动位数的过程。为了方便,后面的例子中仅展示num取有效位(计算移动位数)的过程,不展示移位过程。相信移位的过程对所有人来说都是相对简单的。
① -2 << 4 = -32
分析: value = -2,是负数,那么想要得到补码需要进行转换。再次强调所有的移位操作必须在补码的基础上进行。另外上述式子中value没有指定是long类型,那么就是int类型(java中数字后面带L才是long类型)。此时num转换为补码后,后五位有效。num = 4,是正数,补码和原码一致。截取后五位,情形如下图所示:

② 2 << 33 = 4
分析:上述式子中value = 2,没有指定是long类型,那么value就是int类型。所以对于num来说,转换为补码后,后五位有效。num = 33,是正数,那么它的补码和原码一致,取后五位,情形如下图所示。所以上述式子与"2 << 1"是完全等价的。"2 << 1 = 4",那么"2 << 33 = 4 "。

③ 2 << -15 = 262144
分析:上述式子中value=2,int类型,那么对于num来说自然也是补码的后五位有效。此时num = -15,是负数,所以需要通过转换得到补码,然后再取后五位,情形如下图所示。所以上述式子与"2 << 17"等价。"2 << 1"等于22,那么"2 << 17"相当于218 = 262144。
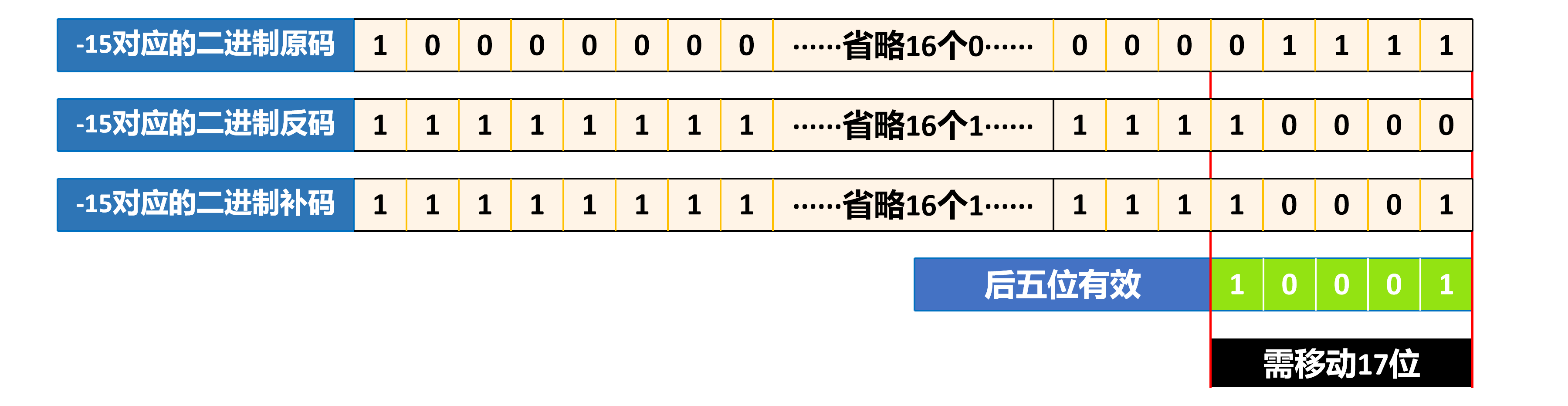
④ 2L << -15 = 1125899906842624
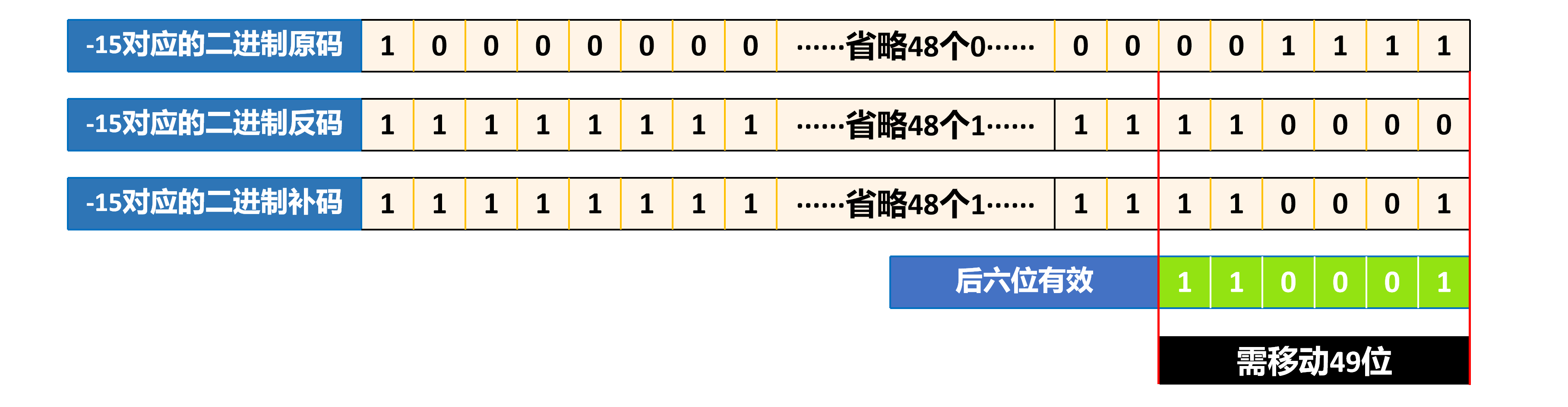
分析:这里和前三个不一样的地方在于value = 2L,是long类型(java中数字后面加"L"或者"l"(小写L)都可以表示一个数是long类型,但是一般不允许使用小写,因为和数字1肉眼不好区分)。那么num的取值就是低六位有效,情形如下所示。所以上述式子与"2 << 49"等价。相当于250 = 1125899906842624。
5、带符号右移(>>)
带符号右移,顾名思义就是数据整体需要往带着符号往右边移动,那么高位就需要补充数据(前面的带符号左移是低位补0)。这里不能像左移一样直接补0,而是需要根据移动之前的符号位来决定补0还是补1。
如果移动之前符号位为0,那么就补0;如果符号位是1,那么就补1
① 8 >> 2 = 2

② 8 >> -64 = 8

③ -8 >> 2

6、无符号右移(>>>)
无符号右移的意思不是不移动符号位,而是无论符号位是1还是0,最高位都补0。由于最高位补0,所以无符号右移最大的特点就是结果一定不是负数。下面针对无符号右移举几个例子:
① -2 >>> 2

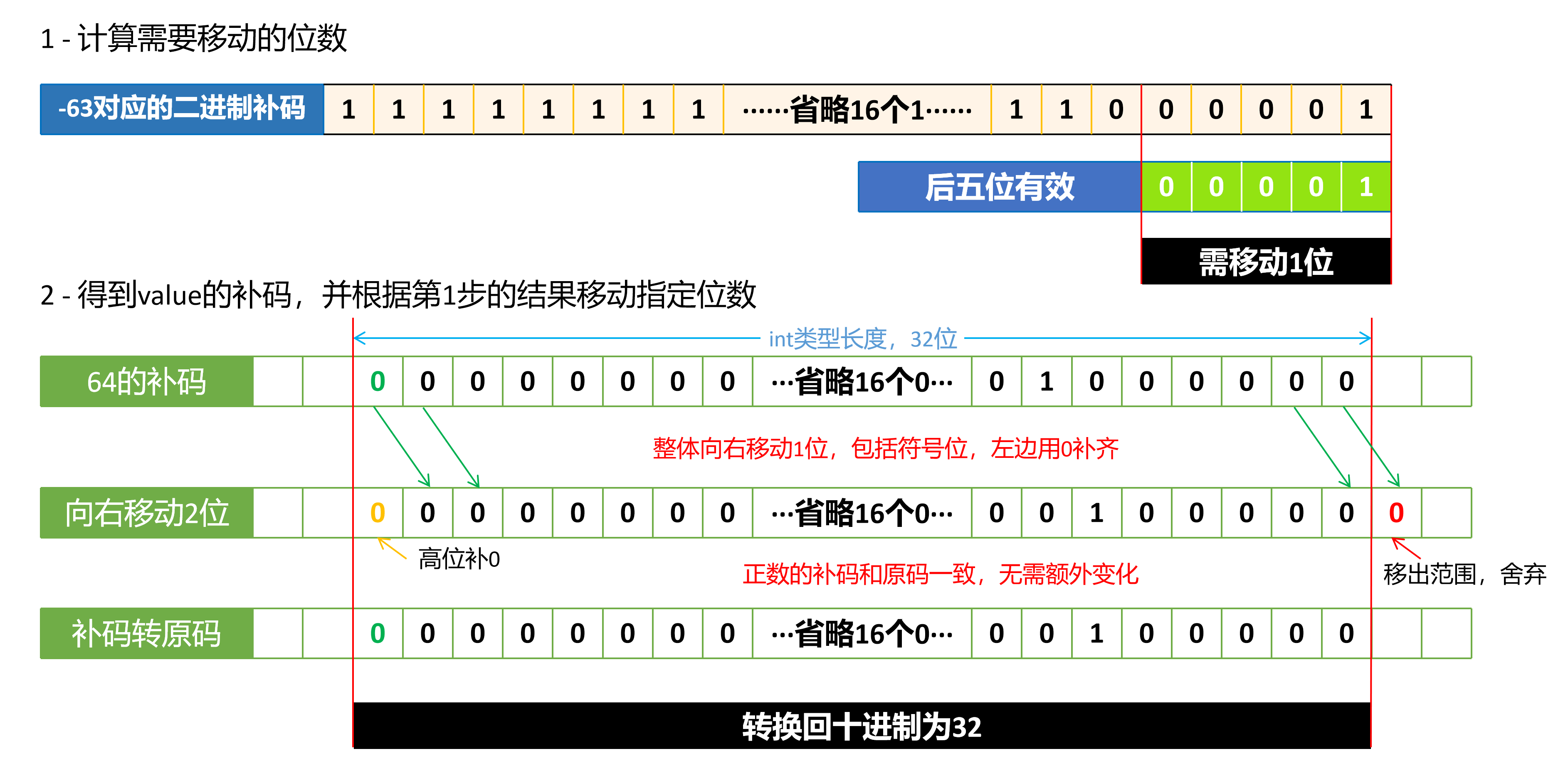
② 64 >>> -63
7、总结
从上面几个示例中,可以总结出移位运算一般情况下正确的操作姿势:
1 - 将num变为补码形式,并根据value的类型决定是取后五位还是后六位,这五位(或六位)数的大小,决定了value需要移动的位数;
2 - 将value变为补码形式,准备移位;
3 - 根据运算符和第1步中得到的移动位数来移动第2步中得到的value的补码;
4 - 将移位之后的结果转换为原码并输出形成最终结果。