题目链接:https://atcoder.jp/contests/abc120
A Favorite Sound
分析:答案为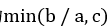 。
。
代码:

1 #include <iostream> 2 3 using namespace std; 4 5 int main() 6 { 7 int a, b, c; 8 cin>>a>>b>>c; 9 cout<<min(b / a, c)<<endl; 10 return 0; 11 }
B K-th Common Divisor
分析:A、B范围很小,枚举即可。注意要判断A、B的大小,从大到小枚举。
代码:

1 #include <cstdio> 2 #include <iostream> 3 4 using namespace std; 5 6 int main() 7 { 8 int a, b, k; 9 scanf("%d %d %d", &a, &b, &k); 10 int imax = max(a, b); 11 int cnt = 0; 12 for(int i = imax; i >= 1; --i) 13 { 14 if(a % i == 0 && b % i == 0) 15 cnt++; 16 if(cnt == k) 17 { 18 printf("%d ", i); 19 break; 20 } 21 } 22 return 0; 23 }
C Unification
分析:因为S串里只有‘0’和‘1’,所以无论如何只要还有‘0’和‘1’同时存在,就一定可以继续该操作。答案就是‘0’和‘1’的数量取最小值的两倍(一次操作两个cube)。
代码:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 5 using namespace std; 6 7 int main() 8 { 9 char s[100005]; 10 scanf("%s", s); 11 int slen = strlen(s); 12 int zero = 0, one = 0; 13 for(int i = 0; i < slen; ++i) 14 { 15 if(s[i] == '0') 16 zero++; 17 else if(s[i] == '1') 18 one++; 19 } 20 printf("%d ", min(zero, one)*2); 21 return 0; 22 }
分析:建边后删边判断连通比较麻烦。我们可以考虑倒着建边。当所有边都删完后,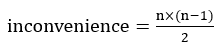 。然后倒序加入每一条边,inconvenience减去加入一条边后连通的点对。判断是否在同一个连通集里可以用并查集维护。这里需要开一个数组s记录每一个集合内的点个数,初始所有点为1.之后更新的时候只要更新并查集里的根节点个数即可。每加一条边
。然后倒序加入每一条边,inconvenience减去加入一条边后连通的点对。判断是否在同一个连通集里可以用并查集维护。这里需要开一个数组s记录每一个集合内的点个数,初始所有点为1.之后更新的时候只要更新并查集里的根节点个数即可。每加一条边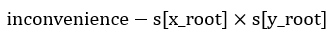 。
。
代码:

1 #include <iostream> 2 #include <cstdio> 3 4 using namespace std; 5 6 typedef long long ll; 7 8 struct bridge 9 { 10 int a; 11 int b; 12 }dict[100005]; 13 14 int parent[100005], trank[100005]; 15 ll sum; 16 ll ans[100005] = {0}; 17 ll s[100005]; 18 19 void init() 20 { 21 for(int i = 0; i < 100005; ++i) 22 { 23 parent[i] = -1; 24 trank[i] = 0; 25 } 26 } 27 28 int find_root(int x) 29 { 30 int x_root = x; 31 while(parent[x_root] != -1) 32 x_root = parent[x_root]; 33 return x_root; 34 } 35 36 int union_set(int x, int y) 37 { 38 int x_root = find_root(x); 39 int y_root = find_root(y); 40 if(x_root == y_root) 41 return 0; 42 else 43 { 44 if(trank[x_root] > trank[y_root]) 45 { 46 parent[y_root] = x_root; 47 sum -= s[x_root]*s[y_root]; 48 s[x_root] += s[y_root]; 49 } 50 else if(trank[y_root] > trank[x_root]) 51 { 52 parent[x_root] = y_root; 53 sum -= s[x_root]*s[y_root]; 54 s[y_root] += s[x_root]; 55 } 56 else 57 { 58 parent[y_root] = x_root; 59 trank[x_root]++; 60 sum -= s[x_root]*s[y_root]; 61 s[x_root] += s[y_root]; 62 } 63 } 64 return 1; 65 } 66 67 int main() 68 { 69 init(); 70 int n, m; 71 scanf("%d %d", &n, &m); 72 for(int i = 0; i < m; ++i) 73 scanf("%d %d", &dict[i].a, &dict[i].b); 74 for(int i = 0; i <= n; ++i) 75 s[i] = 1; 76 sum = 1ll*n*(n-1)/2; 77 for(int i = m - 1; i >= 0; --i) 78 { 79 ans[i] = sum; 80 int x = dict[i].a; 81 int y = dict[i].b; 82 union_set(x, y); 83 } 84 for(int i = 0; i < m; ++i) 85 cout<<ans[i]<<endl; 86 return 0; 87 }
