Lesson2 基于表格法求解RL

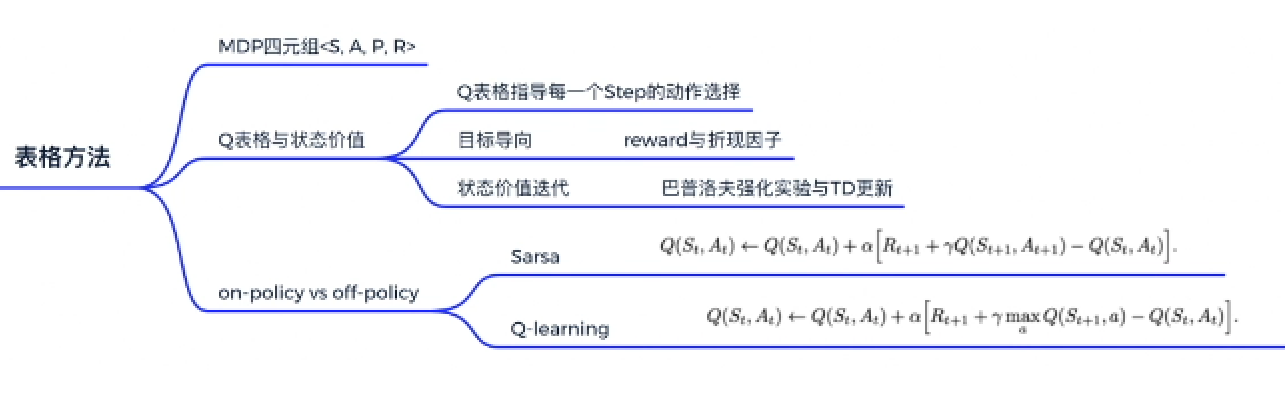
基于表格法求解RL 中相关概念

	含义
S	state 状态(observe)
A	action 动作
R	reward 奖励
P	probability 状态转移概率
MDP	Markov Decision Processes 马尔科夫决策过程(强化学习的基本框架)
TD	Temporal Difference 时序差分（TD单步更新）
on-policy
off-policy

• 强化学习MDP四元组<S,A,P,R>

  (p[s_{t+1},r_t|s_t,a_t])：状态转移概率，下一时刻状态仅取决于这一时刻状态。(s_t)状态下选择(a_t)动作转移到(s_{t+1})并拿到(r_t)的概率，该过程成为MDP。

• 描述环境的方法

  • P函数：probability function: (p[s_{t+1},r_t|s_t,a_t])
  • R函数：reward function：(r[s_t,a_t])

• model-base ：P函数与R函数已知

• model-free ：P函数与R函数未知；试错探索

• Q表格：状态动作价值（一本生活手册），某一状态下不同动作对应的收益大小。

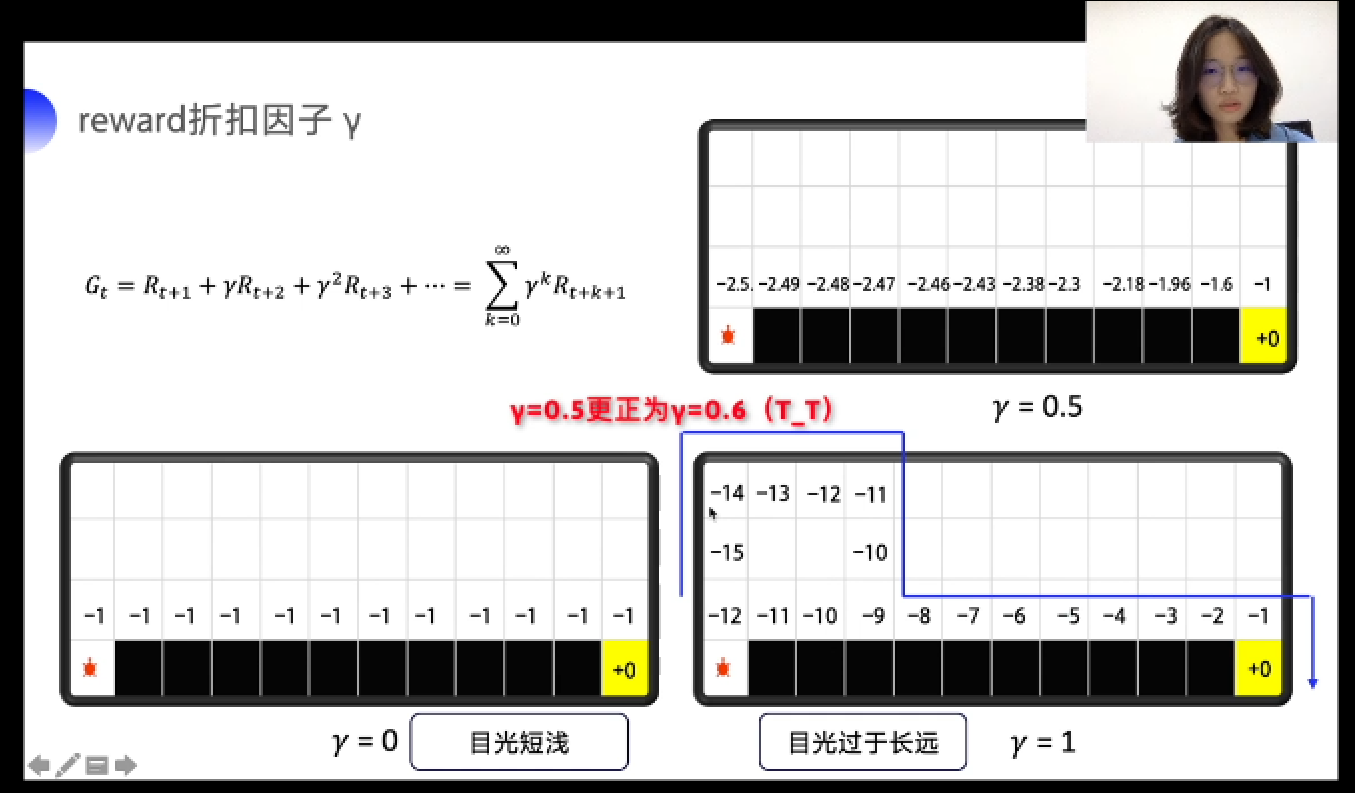
• reward衰减因子(gamma):未来总收益(G_t = R_{t+1}+gamma R_{t+2}+ {gamma}^2 R_{t+3}+...=sum_{k=0}^{infty}gamma ^k R_{t+k+1})

  

• 强化概念：物理意义-巴普洛夫的条件反射实验：反复将条件刺激与无条件刺激在时间上紧密结合，最终条件刺激也能引起无条件反应，形成条件刺激。即，在不断地强化后，上一个状态的价值会影响下一个状态的价值。

  • 上述强化过程称为TD单步更新：(Q(S_t,A_t) ightarrow Q(S,A)+alpha[R_{t+1}+gamma Q(S_{t+1},A_{t+1})-Q(S,A)])，(Q(S_t,A_t))不断地逼近其真实性的未来收益之和。

    

• (epsilon - greedy):一种选择动作的策略，在已知Q表格的情况下，在一定概率下( (epsilon) )下会忽略已有经验随机选取动作，剩余概率下选取收益最高的动作。是一种“利用与探索”相结合的策略。

  	操作
  探索	随机选取动作	(epsilon)
  利用	选取收益最高动作	1-(epsilon)

sarsa

sarsa算法由TD单步更新引入，由于更新Q表格需要t时刻的状态s，对应的动作a，动作奖励r及下一时刻的状态与对应动作a，因此得名sarsa。

算法原理：(Q(S_t,A_t) ightarrow Q(S,A)+alpha[R+gamma Q(S^{'},A^{'})-Q(S,A)])，其中(S^{'})为下一状态，(A^{'})为下一动作。

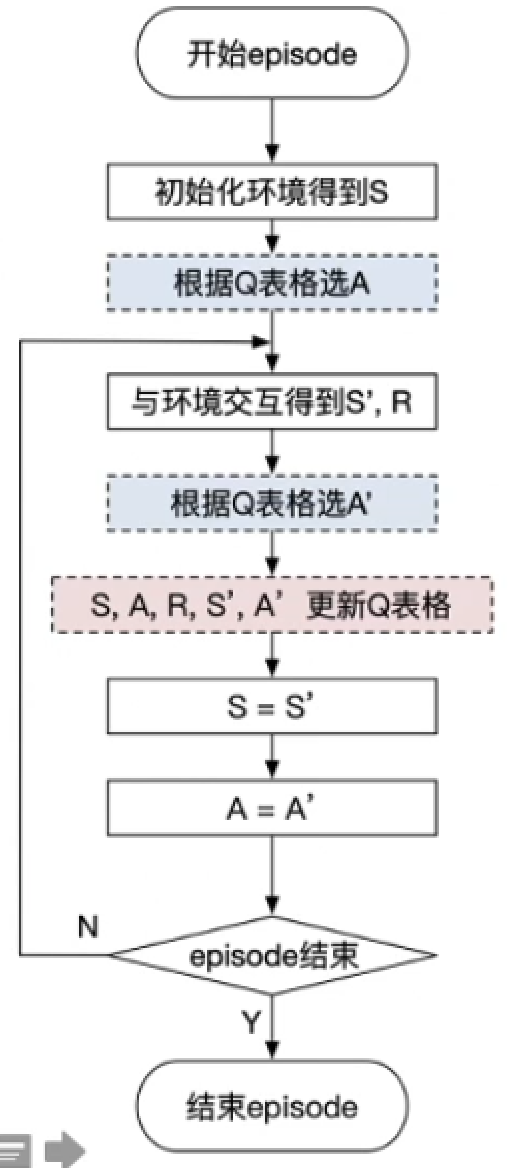
算法流程图如下：

    #----- train.py -----#
    def run_episode(env, agent, render=False):
        total_steps = 0  # 记录每个episode走了多少step
        total_reward = 0
    obs = env.reset()  # 重置环境, 重新开一局（即开始新的一个episode）
    action = agent.sample(obs)  # 根据算法选择一个动作
    
    while True:
        next_obs, reward, done, _ = env.step(action)  # 与环境进行一个交互
        next_action = agent.sample(next_obs)  # 根据算法选择一个动作
        # 训练 Sarsa 算法
        agent.learn(obs, action, reward, next_obs, next_action, done)
    
        action = next_action
        obs = next_obs  # 存储上一个观察值
        total_reward += reward
        total_steps += 1  # 计算step数
        if render:
            env.render()  #渲染新的一帧图形
        if done:
            break
    return total_reward, total_steps
    # ----- agent.py ------ #
    class SarsaAgent(object):
        def __init__(self,
                     obs_n,
                     act_n,
                     learning_rate=0.01,
                     gamma=0.9,
                     e_greed=0.1):
            self.act_n = act_n  # 动作维度，有几个动作可选
            self.lr = learning_rate  # 学习率
            self.gamma = gamma  # reward的衰减率
            self.epsilon = e_greed  # 按一定概率随机选动作
            self.Q = np.zeros((obs_n, act_n))
    
        # 根据输入观察值，采样输出的动作值，带探索
        def sample(self, obs):
            if np.random.uniform(0, 1) < (1.0 - self.epsilon):  #根据table的Q值选动作
                action = self.predict(obs)
            else:
                action = np.random.choice(self.act_n)  #有一定概率随机探索选取一个动作
            return action
    
        # 根据输入观察值，预测输出的动作值
        def predict(self, obs):
            Q_list = self.Q[obs, :]
            maxQ = np.max(Q_list)
            action_list = np.where(Q_list == maxQ)[0]  # maxQ可能对应多个action
            action = np.random.choice(action_list)
            return action
    
        # 学习方法，也就是更新Q-table的方法
        def learn(self, obs, action, reward, next_obs, next_action, done):
            """ on-policy
                obs: 交互前的obs, s_t
                action: 本次交互选择的action, a_t
                reward: 本次动作获得的奖励r
                next_obs: 本次交互后的obs, s_t+1
                next_action: 根据当前Q表格, 针对next_obs会选择的动作, a_t+1
                done: episode是否结束
            """
            predict_Q = self.Q[obs, action]
            if done:
                target_Q = reward  # 没有下一个状态了
            else:
                target_Q = reward + self.gamma * self.Q[next_obs,
                                                        next_action]  # Sarsa
            self.Q[obs, action] += self.lr * (target_Q - predict_Q)  # 修正q

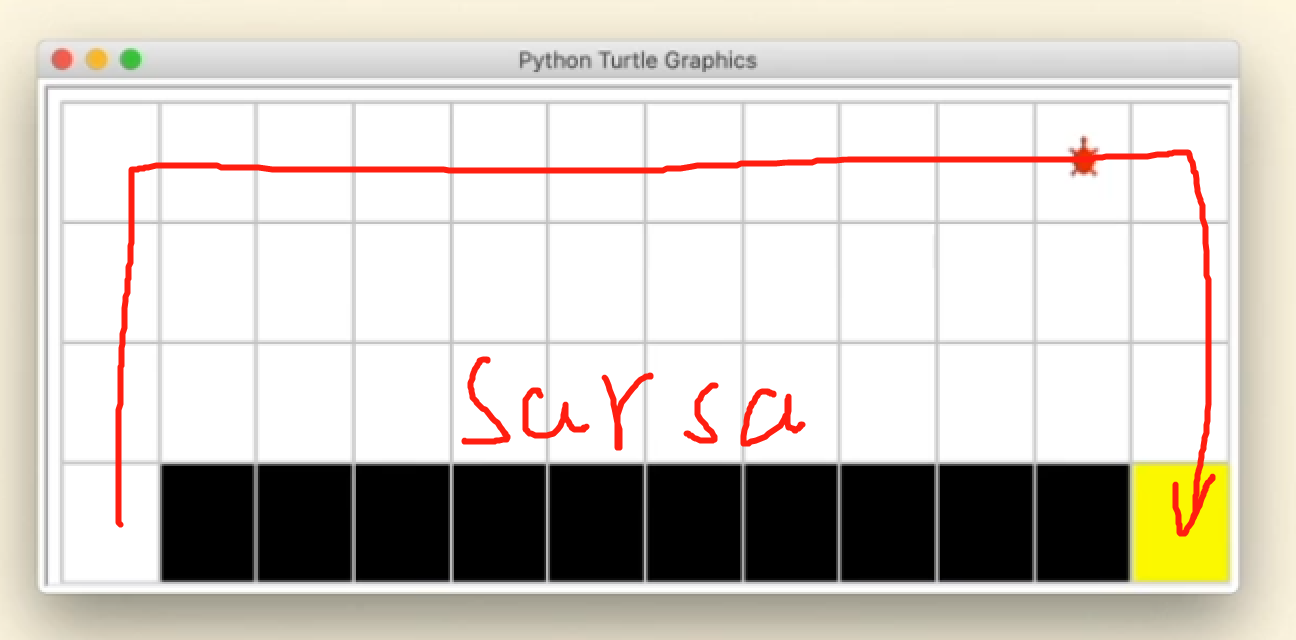
最终sarsa的结果如下，会远离悬崖，因为agent在行动时有一定概率会探索，因此考虑到这个因素，sarsa会远离悬崖。因为，sarsa为on-policy的策略。

on/off - policy 与 Q-learning

1. on-policy 与 off-policy

on/off-policy 是两种不同的学习策略，sarsa属于on-policy。

• on-policy：用下一步“实际会执行的动作”来优化Q表格，选取动作与优化Q表格使用同一种策略。可结合上述sarsa实验结果说明，由于小乌龟选取动作使用(epsilon - greedy)策略，因此sarsa知道自己处于悬崖边时有可能会坠入悬崖，因此优化时就会远离悬崖。

• off-policy：选取动作时使用行为策略(behavior policy)，优化目标时使用目标策略(target policy)。由于探索与利用时使用不同策略，因此off-policy可以尽情试错探索，相较于on-policy会更大胆一些。Q-learning算法就属于off-policy。

  

  使用off-policy更容易获得最优策略

  

2.Q-learning VS Sarsa

Q-learning更新表格代码如下：

# 学习方法，也就是更新Q-table的方法
def learn(self, obs, action, reward, next_obs, done):
    """ off-policy
            obs: 交互前的obs, s_t
            action: 本次交互选择的action, a_t
            reward: 本次动作获得的奖励r
            next_obs: 本次交互后的obs, s_t+1
            done: episode是否结束
        """
    predict_Q = self.Q[obs, action]
    if done:
        target_Q = reward  # 没有下一个状态了
        else:
            target_Q = reward + self.gamma * np.max(
                self.Q[next_obs, :])  # Q-learning
            self.Q[obs, action] += self.lr * (target_Q - predict_Q)  # 修正q

Q-learning与sarsa区别于优化中Target值得计算，sarsa用自身算法产生的动作进行优化Q表格；Q-learning不需要知道下一步动作，直接选取最佳策略来优化Q表格。

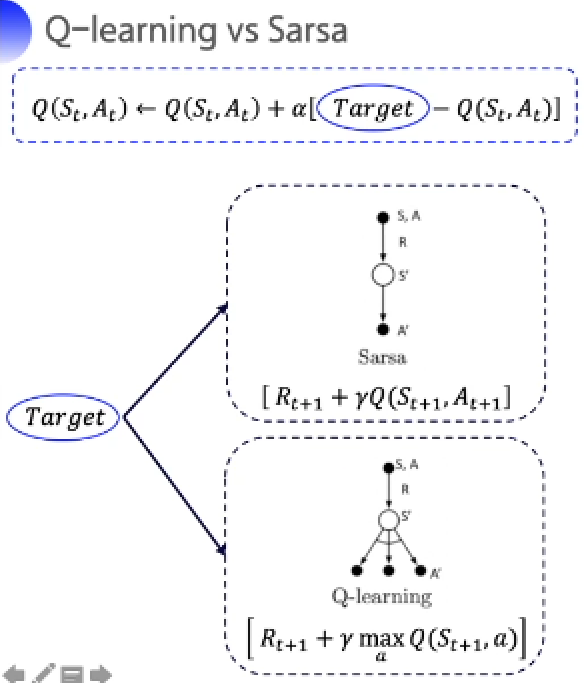
经过对比可知，Sarsa与Q-learning仅在Target处计算有所不同。Target的计算式为(G_t=R_{t+1}+gamma G_{t+1})，两种算法对于(G_{t+1})的计算有所不同：Q-learning使用两种策略，更新Q表格式的目标策略会逼近最佳策略。

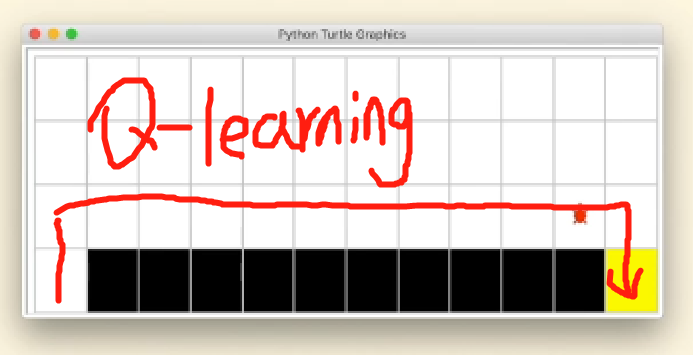
3.总结