一、二叉树的遍历的定义
1.二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问依次且仅被访问依次。树的结点之间不存在唯一的前驱和后继关系,在访问一个结点后,下一个被访问的结点面临着不同的选择,因此,二叉树有多种遍历方法。这多种遍历方法,其实都是把非线性结构的二叉树编程线性序列,从而可以确定二叉树中某个指定结点在某种遍历序列中的前驱和后继。
2.二叉树遍历的性质:
- 已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
- 已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
- 已知前序遍历序列和后序遍历序列,不可以唯一确定一棵二叉树。
二、二叉树递归遍历方法
1.前序遍历
若二叉树为空,则空操作返回;否则
- 先访问根结点
- 前序遍历左子树
- 前序遍历右子树
(1)例如(双亲-左结点-右结点)
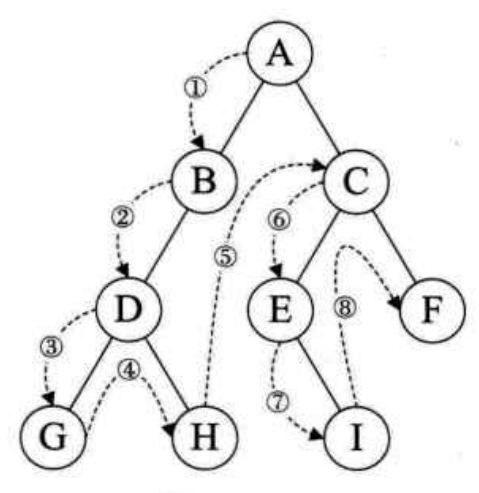
前序遍历的顺序为:ABDGHCEIF
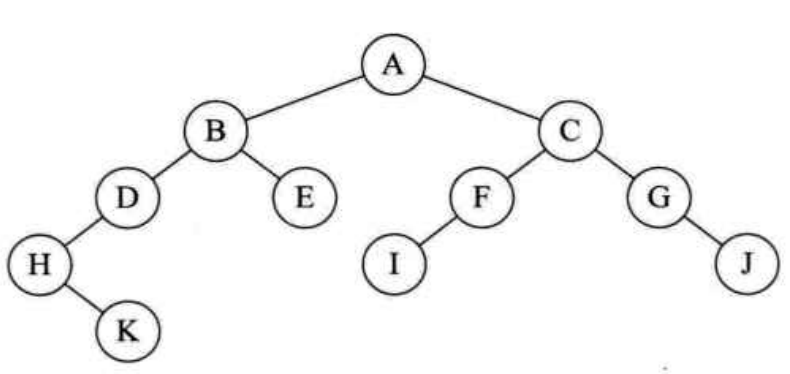
(2)以下面的二叉树T为例分析代码:

1 /* 前序递归遍历T */ 2 void PreOrderTraverse(BiTree T) 3 { 4 if(T==NULL) 5 return; 6 printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */ 7 PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */ 8 PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */ 9 }
最后顺序为:ABDHKECFIGJ
1.T为A, 二叉树T根结点不为null,执行第6行程序,打印A,进入T为A的7
2.T为A, 执行第7行程序,访问结点A的左孩子,执行第4行程序判断A的左孩子不为空,执行第6行程序,打印B,进入T为B的7
3.T为B, 执行第7行程序,访问结点B的左孩子,执行第4行程序判断B的左孩子不为空,执行第6行程序,打印D,进入T为D的7
4.T为D, 执行第7行程序,访问结点D的左孩子,执行第4行程序判断D的左孩子不为空,执行第6行程序,打印H,进入T为H的7
5.T为H, 执行第7行程序,访问结点H的左孩子,执行第4行程序判断H的左孩子为null,return掉,进入H的右孩子的8
6.T为H, 执行第8行程序,访问结点H的右孩子,执行第4行程序判断H的右孩子不为空,执行第6行程序,打印K,进入T为K的8
7.T为K, 执行第7行程序,访问结点K的左孩子,执行第4行程序判断K的左孩子为null,return掉,进入K的的8
8.T为K, 执行第8行程序,访问结点K的右孩子,执行第4行程序判断K的右孩子为null,return掉,执行完毕,到6,执行完毕,到4,进入T为D的8
9.T为D, 执行第8行程序,访问结点D的右孩子,执行第4行程序判断D的右孩子为null,return掉,执行完毕,到3
10.T为B,执行第8行程序,访问结点B的右孩子,执行第4行程序判断B的右孩子不为空,执行第6行程序,打印E,进入T为E的7
11.T为E,执行第7行程序,访问结点E的左孩子,执行第4行程序判断E的左孩子为null,return掉,进入E的8
12.T为E,执行第8行程序,访问结点E的左孩子,执行第4行程序判断E的右孩子为null,return掉,执行完毕,到10,执行完毕,到2,进入T为A的8
...
2.中序遍历
若二叉树为空,则空操作返回;否则
- 中序遍历左子树
- 访问根结点
- 中序遍历右子树
(1)例如(左孩子-双亲-右孩子)

中序遍历的顺序为:GDHBAEICF
(2)以下面的二叉树T为例分析代码:
1 /*中序递归遍历T */ 2 void InOrderTraverse(BiTree T) 3 { 4 if(T==NULL) 5 return; 6 InOrderTraverse(T->lchild); /* 中序遍历左子树 */ 7 printf("%c",T->data); /* 显示结点数据,可以更改为其它对结点操作 */ 8 InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */ 9 }
最后结果为:HKDBEAIFCGJ
1.T为A, 二叉树T根结点不为null,执行第6行程序,进入T为A的6
2.T为A, 执行第6行程序,访问结点A的左孩子,执行第4行程序判断A的左孩子不为空,进入T为B的6
3.T为B, 执行第6行程序,访问结点B的左孩子,执行第4行程序判断B的左孩子不为空,进入T为D的6
4.T为D, 执行第6行程序,访问结点D的左孩子,执行第4行程序判断D的左孩子不为空,进入T为H的6
5.T为H, 执行第6行程序,访问结点H的左孩子,执行第4行程序判断H的左孩子为空,return掉,到4,T为H,执行第7行程序,打印H,进入T为H的8
6.T为H, 执行第8行程序,访问结点H的右孩子,执行第4行程序判断H的右孩子不为空,进入T为K的6
7.T为K, 执行第6行程序,访问结点K的左孩子,执行第4行程序判断K的左孩子为空,return掉,到6,T为k,执行第7行程序,打印K,进入T为K的8
8.T为K, 执行第8行程序,访问结点K的右孩子,执行第4行程序判断K的右孩子为空,return掉,执行完毕,到6,执行完毕,到4,进入T为D的8
9.T为D, 执行第8行程序,访问结点D的右孩子,执行第4行程序判断D的右孩子为空,return掉,执行完毕,到3
10.T为B,执行第8行程序,访问结点B的右孩子,执行第4行程序判断B的右孩子不为空,进入T为E的6
11.T为E,执行第6行程序,访问结点E的左孩子,执行第4行程序E判断的左孩子为空,return掉,到10,T为E,执行第7行程序,打印E,进入T为E的8
12.T为E,执行第8行程序,访问结点E的右孩子,执行第4行程序判断E的右孩子为空,return掉,执行完毕,到10,执行完毕,到2,进入T为A的8
...
3.后序遍历
若二叉树为空,则空操作返回;否则
- 先叶子后结点的方式遍历访问左子树
- 先叶子后结点的方式遍历访问右子树
- 访问根结点
(1)例如(左结点-右结点-双亲)
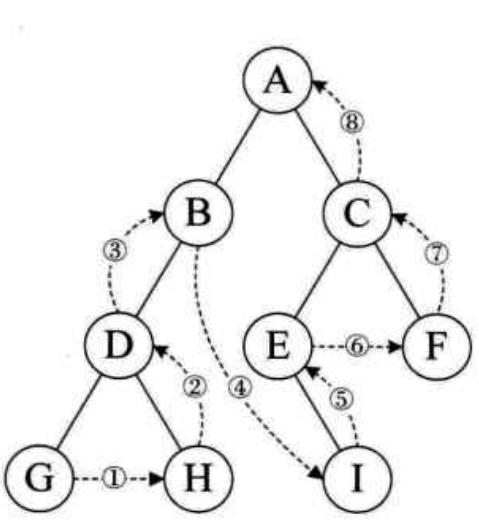
后序遍历的顺序为:GHDBIECFA
(2)以下面的二叉树T为例分析代码:

1 /* 后序递归遍历T */ 2 void PostOrderTraverse(BiTree T) 3 { 4 if(T==NULL) 5 return; 6 PostOrderTraverse(T->lchild); /* 先后序遍历左子树 */ 7 PostOrderTraverse(T->rchild); /* 再后序遍历右子树 */ 8 printf("%c",T->data); /* 显示结点数据,可以更改为其它对结点操作 */ 9 }
最后结果为:KHDEBIFJGCA
1.T为A, 二叉树T根结点不为null,执行第6行程序,进入T为A的6
2.T为A, 执行第6行程序,访问结点A的左孩子,执行第4行程序判断A的左孩子不为空,进入T为B的6
3.T为B, 执行第6行程序,访问结点B的左孩子,执行第4行程序判断B的左孩子不为空,进入T为D的6
4.T为D, 执行第6行程序,访问结点D的左孩子,执行第4行程序判断D的左孩子不为空,进入T为H的6
5.T为H, 执行第6行程序,访问结点H的左孩子,执行第4行程序判断H的左孩子为空,return掉,到4,进入T为H的7
6.T为H, 执行第7行程序,访问结点H的右孩子,执行第4行程序判断H的右孩子不为空,进入T为K的6
7.T为K, 执行第6行程序,访问结点K的左孩子,执行第4行程序判断K的左孩子为空,return掉,到6,进入T为K的7
8.T为K, 执行第7行程序,访问结点K的右孩子,执行第4行程序判断K的右孩子为空,return掉,到7,T为K,执行第8行程序,打印K,执行完毕,到6,执行完毕,到6,T为H,执行第8行程序,打印H,执行完毕,到4,进入T为D的7
9.T为D, 执行第7行程序,访问结点D的右孩子,执行第4行程序判断D的右孩子为空,return掉,到9,T为D,执行第8行程序,打印D,执行完毕,到3,进入T为B的7
10.T为B,执行第7行程序,访问结点B的右孩子,执行第4行程序判断B的右孩子不为空,进入T为E的6
11.T为E,执行第6行程序,访问结点E的左孩子,执行第4行程序E判断的左孩子为空,return掉,到10,进入T为E的7
12.T为E,执行第7行程序,访问结点E的右孩子,执行第4行程序判断E的右孩子为空,return掉,到11,执行完毕,到10,T为E,执行第8行程序,打印E,执行完毕,到10,T为B,执行第8行程序,打印B,执行完毕,到1,进入T为A的7
...
4.层序遍历
若二叉树为空,则空操作返回;否则
- 先访问根结点
- 从左到右依次访问第i(从根结点下面一层开始)层的每一个结点
- 从左到右依次访问第i+1层的每一个结点
(1)例如

层序遍历的顺序为:ABCDEFGHI
三、二叉树递归遍历算法的Java代码实现(二叉树链式存储结构):
package bigjun.iplab.linkBiTree;
import bigjun.iplab.linkQueue.LinkQueue;
import bigjun.iplab.linkStack.LinkStack;
/**
* 二叉树的链式存储结构-二叉链表存储结构
* 前序、中序、后序三种遍历算法的递归实现
*/
public class LinkBiTree {
private BiTreeNode root;
// 构造方法1: 构造一棵空树
public LinkBiTree() {
this.root = null;
}
// 构造方法2: 构造一棵非树
public LinkBiTree(BiTreeNode root) {
this.root = root;
}
// 先序递归遍历算法
public void preOrderTraverse(BiTreeNode T) {
if (T != null) {
System.out.print(T.data);
preOrderTraverse(T.lchild);
preOrderTraverse(T.rchild);
}
}
// 中序递归遍历算法
public void inOrderTraverse(BiTreeNode T) {
if (T != null) {
inOrderTraverse(T.lchild);
System.out.print(T.data);
inOrderTraverse(T.rchild);
}
}
// 后序递归遍历算法
public void postOrderTraverse(BiTreeNode T) {
if (T != null) {
postOrderTraverse(T.lchild);
postOrderTraverse(T.rchild);
System.out.print(T.data);
}
}
// 采用构造方法来构造二叉树
public LinkBiTree createLinkBiTree() {
BiTreeNode k = new BiTreeNode('K'); // 要先定义孩子,因为程序是按先后顺序执行的
BiTreeNode i = new BiTreeNode('I');
BiTreeNode j = new BiTreeNode('J');
BiTreeNode e = new BiTreeNode('E');
BiTreeNode h = new BiTreeNode('H', null, k);
BiTreeNode f = new BiTreeNode('F', i, null);
BiTreeNode g = new BiTreeNode('G', null, j);
BiTreeNode d = new BiTreeNode('D', h, null);
BiTreeNode c = new BiTreeNode('C', f, g);
BiTreeNode b = new BiTreeNode('B', d, e);
BiTreeNode a = new BiTreeNode('A', b, c);
return new LinkBiTree(a);
}
public static void main(String[] args) throws Exception {
LinkBiTree linkBiTree = new LinkBiTree(); // 创建一棵空树
LinkBiTree biTree = linkBiTree.createLinkBiTree(); // 调用创造方法创造根结点为a的二叉树
BiTreeNode root = biTree.root; // 取得二叉树的根结点
System.out.print("先序递归遍历算法得到的序列为: ");
linkBiTree.preOrderTraverse(root);
System.out.println();
System.out.print("中序递归遍历算法得到的序列为: ");
linkBiTree.inOrderTraverse(root);
System.out.println();
System.out.print("后序递归遍历算法得到的序列为: ");
linkBiTree.postOrderTraverse(root);
System.out.println();
}
}
- 输出:
先序递归遍历算法得到的序列为: ABDHKECFIGJ
中序递归遍历算法得到的序列为: HKDBEAIFCGJ
后序递归遍历算法得到的序列为: KHDEBIFJGCA