NOIP2007树网的核 分析性质+树的直径。

NOIP2007树网的核

Solution：

引理：当路径F为直径时，树的偏心距最小

证明：

先给一张图吧，方便发挥（口胡）一点：

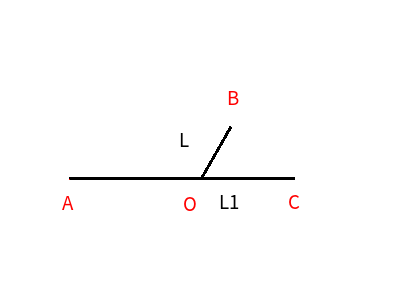
设直径为D（即AOC），ECC[D]=L,设另外一条路径为F1（即AOB）。

假设ECC[F1]<=ECC[D]，

由直径的性质可知：O点右侧任意一点到O的距离Li<=L1，且L<=L1        

那么可以得到：ECC[F1]=L1
    
那么结合假设 可以得到：L=ECC[D]>=ECC[F1]=L1   

∴ L1=L，那么当ECC[F1]为答案时，ECC[D]也为答案，且此时答案最小。
    
可以发现，对于其他任意一条路径Fi，此恒成立。

证毕。

所以我们考虑任意求一条直径，再枚举直径上一段(di,dj)，则

ans=min{ans,max{max{dep(di,dj)},dis(d1,di),dis(dj,dN)}};

dep直径外一点到直径的最小距离。

由于max{dep(di~dj)}为定值ECC[D]，所以我们可以使两边尽量小，即在不超过限制的前提下，核越长越好。

Code↓：

#include<bits/stdc++.h>
#define RG register
#define IL inline
#define LL long long
#define DB double
using namespace std;

IL int gi() {
   RG int x=0,w=0; char ch=getchar();
   while (ch<'0'||ch>'9') {if (ch=='-') w=1;ch=getchar();}
   while (ch>='0'&&ch<='9') x=x*10+(ch^48),ch=getchar();
   return w?-x:x;
}

const int N=5e5+10;

int n,s,S,L,R,cnt,ans=N,tot,head[N],fa[N],dis[N],dia[N],tag[N],d[N],ver[N];

struct EDGE{int next,to,ver;}e[N<<1];
IL void make(int a,int b,int c) {
    e[++tot]=(EDGE){head[a],b,c},head[a]=tot;
    e[++tot]=(EDGE){head[b],a,c},head[b]=tot;
}

void dfs(int x,int fx) {
    RG int i,y;
    for (i=head[x],fa[x]=fx;i;i=e[i].next) 
        if ((y=e[i].to)!=fx) dis[y]=dis[x]+e[i].ver,dfs(y,x);
}

void DFS(int x,int fx) {
    RG int i,y;
    for (i=head[x];i;i=e[i].next)
        if ((y=e[i].to)!=fx&&!tag[y]) DFS(y,x),d[x]=max(d[x],d[y]+e[i].ver);
    for (i=head[x];i;i=e[i].next)	
        if ((y=e[i].to)!=fx&&tag[y]) ver[y]=e[i].ver,DFS(y,x);	
}

int main()
{	
    RG int i,j,x,y,z,MAX;
    n=gi(),s=gi();
    for (i=1;i<n;++i) x=gi(),y=gi(),z=gi(),make(x,y,z);
    for (i=1,dfs(1,0),MAX=0;i<=n;++i)
        if (dis[i]>MAX) MAX=dis[i],S=i;
    for (i=1,dis[S]=0,dfs(S,0),MAX=0;i<=n;++i)
        if (dis[i]>MAX) MAX=dis[i],S=i;
    while (S) dia[++cnt]=S,tag[S]=1,S=fa[S];
    for (i=cnt,DFS(dia[cnt],0),MAX=0;i>=1;--i) MAX=max(MAX,d[dia[i]]),ver[dia[i]]+=ver[dia[i+1]];
    for (L=1,R=1;L<=cnt&&R<=cnt;++L) {
        while (R<cnt&&ver[dia[L]]-ver[dia[R+1]]<=s) ++R;
        ans=min(ans,max(MAX,max(ver[dia[1]]-ver[dia[L]],ver[dia[R]])));
    }
    printf("%d
",ans);
    return 0;
}

The End