图基本的表示方式为邻接矩阵和邻接表,而且两者可以相互转化,本文将讨论简单图(结点没有到本身的边)的表示和遍历以及最小生成树的算法。
1.图的定义表示
#define _CRT_SECURE_NO_DEPRECATE
#include<stdio.h>
#include<stdlib.h>
#include<windows.h>
#define DataType char
#define QueueType int
#define StackType int
const int un = 65535;//边界常量,表示两点之间没有边
const int Maxsize = 10;//图结点最大值
const int MaxEdge = 50;//边最大值
boolean visited[Maxsize];//访问标识数组,用于遍历
//图的邻接矩阵结构定义
typedef struct
{
DataType vertex[Maxsize];//结点数组
int arc[Maxsize][Maxsize];//邻接矩阵
int vertexNum, arcNum;//结点数量和边数量
}AdjMatrix, Graph;
//图的邻接表定义
typedef struct ArcNode//邻接表边结点
{
int adjvex;//邻接点域
ArcNode*next;
}ArcNode;
typedef struct //定义邻接表结点
{
DataType vertex;
ArcNode *firstedge;
}VertexNode;
typedef struct //邻接表
{
VertexNode adjlist[Maxsize];//定点结点数组
int vertexNum, arcNum;//顶点数和边数
}AdjList;
2.邻接表与邻接矩阵转化
这里邻接矩阵只用1表示两个图结点之间有边,0表示没有边。
给出一个有向图(无向图类似):

邻接矩阵:

邻接表:
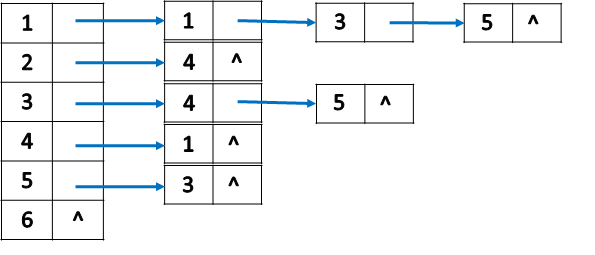
两种表示方式的转换:
//邻接矩阵转换为邻接表
void MatToList(AdjMatrix &A, AdjList &B)
{
B.vertexNum = A.vertexNum;
B.arcNum = A.arcNum;
ArcNode *p;//边结点临时变量
for (int i = 0; i < A.vertexNum; i++)
{
B.adjlist[i].vertex = A.vertex[i];
B.adjlist[i].firstedge = NULL;
}
for (int i = 0; i < A.vertexNum;i++)//双循环找邻接矩阵所有边
for (int j = 0; j < A.vertexNum; j++)
{
if (A.arc[i][j] != 0)
{
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;
p->next = B.adjlist[i].firstedge;//头插法
B.adjlist[i].firstedge = p;
}
}
}
//邻接表转为邻接矩阵
void ListToMat(AdjMatrix &A, AdjList &B)
{
A.vertexNum = B.vertexNum;
A.arcNum = B.arcNum;
ArcNode *p;
for (int i = 0; i < A.vertexNum; i++)
for (int j = 0; j < A.vertexNum; j++)
A.arc[i][j] = 0;
for (int i = 0; i < A.vertexNum; i++)
{
p = B.adjlist[i].firstedge;
while (p)
{
A.arc[i][p->adjvex] = 1;
p = p->next;
}
}
}
3.有向图邻接表建立逆邻接表
void List(AdjList A, AdjList &B)
{
B.vertexNum = A.vertexNum;
B.arcNum = A.arcNum;
ArcNode* p,*q;
for (int i = 0; i < A.vertexNum; i++)
B.adjlist[i].firstedge = NULL;
for (int i = 0; i < A.vertexNum; i++)//头单链表插法来构造
{
p = A.adjlist[i].firstedge;
while (p)
{
q = (ArcNode*)malloc(sizeof(ArcNode));
q->adjvex = i;
q->next = B.adjlist[p->adjvex].firstedge;
B.adjlist[p->adjvex].firstedge=q;
p = p->next;
}
}
}
4.统计出度
//统计出度为0的算法邻接矩阵(入度统计出度)
int SumZero(AdjMatrix &A)
{
int i, j;
int count = 0;
for (i = 0; i < A.vertexNum; i++)
{
for (j = 0; j < A.vertexNum; j++)
{
if (A.arc[i][j] != 0)
break;
}
if (j >= A.vertexNum)
count++;
}
return count;
}
//统计出度为0的算法邻接表(入度可以设置一个数组帮助统计)
int SumZero(AdjList &A)
{
int i;
int count = 0;
for (i = 0; i < A.vertexNum; i++)
{
if(!A.adjlist[i].firstedge)
count++;
}
return count;
}
5.图的遍历邻接矩阵表示法(邻接表类似)
(1)广度优先遍历
广度优先遍历用到队列,类似二叉树的层次遍历,队列在之前的算法中已经定义。
广度优先遍历代码
void BFS_ADJTraverse(AdjMatrix G)//邻接矩阵广度
{
int i, j,t;
SqQueue Q;
for (int i = 0; i < G.vertexNum; i++)
visited[i] = false;
InitQueue(Q);
for (i = 0; i < G.vertexNum; i++)//循环每一个可能的结点,防止是非连通图
{
if (!visited[i])
{
printf("%3c", G.vertex[i]);
visited[i] = true;
Enqueue(Q, i);
while (!QueueEmpty(Q))
{
Dequeue(Q, t);
for (j = 0; j < G.vertexNum; j++)
{
if (G.arc[t][j] == 1 && !visited[j])
{
printf("%3c", G.vertex[j]);
visited[j] = true;
Enqueue(Q, j);
}
}
}
}
}
}
//第二种算法,设置两个函数找邻接点(可以改造一下来针对邻接表,主函数不变)
int FirstNeighborADJ(AdjMatrix G, int vex)
{
int i = 0;
for (i = 0; i < G.vertexNum;i++)
if (G.arc[vex][i] ==1)
break;
return i;//如果没找到则是VertexNum
}
int NextNeighborADJ(AdjMatrix G, int vex, int cur)
{
int i = 0;
for (i = cur+1; i < G.vertexNum; i++)
if (G.arc[vex][i] ==1)
break;
return i;//如果没找到则是VertexNum
}
void BFS_ADJTraverse(AdjMatrix G)//邻接矩阵广度
{
int i, j,t;
SqQueue Q;
for (int i = 0; i < G.vertexNum; i++)
visited[i] = false;
InitQueue(Q);
for (i = 0; i < G.vertexNum; i++)//循环每一个可能的结点,防止是非连通图
{
if (!visited[i])
{
printf("%3c", G.vertex[i]);
visited[i] = true;
Enqueue(Q, i);
while (!QueueEmpty(Q))
{
Dequeue(Q, t);
for (j = FirstNeighborADJ(G, t); j < G.vertexNum; j = NextNeighborADJ(G, t, j))
{
if (!visited[j])
{
printf("%3c", G.vertex[j]);
visited[j] = true;
Enqueue(Q, j);
}
}
}
}
}
}
(2)深度优先遍历,递归方法和非递归方法(非递归用到的栈在之前的算法中已定义)
void DFSADJ(AdjMatrix G, int v)//邻接矩阵深度优先遍历递归,从编号为v的点深度遍历
{
printf("%3c", G.vertex[v]);
visited[v] = true;
for (int i = FirstNeighborADJ(G, v); i < G.vertexNum;i=NextNeighborADJ(G,v,i))
if (!visited[i])
DFSADJ(G, i);
}
void DFS_ADJTraverse(AdjMatrix G)
{
int i;
for (int i = 0; i < G.vertexNum; i++)
visited[i] = false;
for (i = 0; i < G.vertexNum; i++)//循环每一个可能的结点,防止是非连通图
{
if (!visited[i])
DFSADJ(G, i);
}
}
void DFSADJStack(AdjMatrix G, int v)//深度遍历非递归
{
int j, t;
SqStack S;
InitStack(S);
Push(S, v);
visited[v] = true;
printf("%3c", G.vertex[v]);
while (!StackEmpty(S))
{
Pop(S, t);
Push(S, t);
for (j = FirstNeighborADJ(G, t); j < G.vertexNum; j = NextNeighborADJ(G, t, j))
{
if (!visited[j])
{
printf("%3c", G.vertex[j]);
visited[j] = true;
Push(S, j);
break;
}
}
if (j == G.vertexNum)//此时与t结点所有的相连结点都找完了(参照NextNeighborADJ函数),t节点没有可用了,弹栈
Pop(S, t);
}
}
void DFS_ADJTraverseStack(AdjMatrix G)//邻接矩阵深度优先遍历递归
{
int i;
for (int i = 0; i < G.vertexNum; i++)
visited[i] = false;
for (i = 0; i < G.vertexNum; i++)
{
if (!visited[i])
DFSADJStack(G, i);
}
}
//利用深度优先遍历判断是否为树
bool IsTree(Graph G)//判断是否为树,从一点遍历到所有点,且边数n-1
{
for (int i = 0; i < G.vertexNum; i++)
visited[i] = false;
int Vnum = 0, Arcnum = G.arcNum;
if (Arcnum != G.vertexNum - 1)
return false;
int i;
//for (int i = 0; i < G.vertexNum; i++)
// visited[i] = false;
DFSADJStack(G, 0);//从0开始遍历连通变量中所有点,并统计所有访问点的数量(visit[i]==true)
for (i = 0; i < G.vertexNum;i++)
if (visited[i] == true)
Vnum++;
if (Vnum < G.vertexNum)
return false;
else
return true;
}
6.最小生成树算法
用到的加权无向图为

(1)Prim算法,时间复杂度(O(n^2))
(算法思想是按照边的大小来选点,生成树集合中加入新点,关键是定义了一个关联点数组和一个边集数组)
void MinTree_Prim(AdjMatrix G)
{
int i = 0;
int adjvex[Maxsize];//例如{1,2,4,6,3,0}是指该位置顶点分别与1 2 4 6 3 0有联系
int lowarc[Maxsize];//保持相关顶点间的权值,与adjvex相对应
adjvex[0] = 0;
lowarc[0] = 0;//v0加入,开始
for (i = 1; i < G.vertexNum; i++)//初始化为与0的链接关系,边的权值(没有边为un=65535)
{
adjvex[i] = 0;
lowarc[i] = G.arc[0][i];
}
for (i = 1; i < G.vertexNum; i++)//n-1个边中选出最小的
{
int min = un,j=1,k=0;
while (j < G.vertexNum)
{
if (lowarc[j] != 0 && lowarc[j]<min)
{
min = lowarc[j];
k = j;//存储最小的下标
}
j++;
}
printf("%2d--%2d,%3d
", adjvex[k],k, lowarc[k]);
lowarc[k] = 0;//此顶点完成任务,置零
for (j = 1; j < G.vertexNum; j++)//用k行的所有边的值来替代lowarc现有大边,正是prim算法中点逐渐增多的过程
{
if ( G.arc[k][j] < lowarc[j])
{
lowarc[j] = G.arc[k][j];
adjvex[j] = k;
}
}
}
}
(2)Kruskal算法,时间复杂度(O(eloge))
(算法思想是按照点固定,边集合中加入新的小边,关键是定义了一个环路判断函数Find和一个边结构数组)
typedef struct Edge
{
int begin, end;
int weight;
}Edge;//边集
int Find(int parent[], int f)//环路判断函数
{
while (parent[f] > 0)
f = parent[f];
return f;
}
int EdgeCreatSort(Edge edges[], AdjMatrix G)//边集数组按权值排序
{
int n=0,i, j;
Edge temp;
for (i = 0; i < G.vertexNum; i++)
{
for (j = i + 1; j < G.vertexNum; j++)
{
if (G.arc[i][j]!=0&&G.arc[i][j] < un)
{
edges[n].begin = i;
edges[n].end = j;
edges[n].weight = G.arc[i][j];
n++;
}
}
}
for (i = 1; i < n; i++)//插入排序
{
temp = edges[i];
for (j = i - 1; j >= 0 && edges[j].weight > temp.weight; j--)
{
edges[j + 1] = edges[j];
}
edges[j+1 ] = temp;
}
return n ;
}
void MinTree_Kruskal(AdjMatrix G)
{
int i, n, m,edgnum;
Edge edges[MaxEdge];//边集数组
int parent[Maxsize];//定义parent数组用来判断边与边是否构成环路,是否在一棵树上,存放此点所连树的终端节点
edgnum=EdgeCreatSort(edges, G);
for (i = 0; i < G.vertexNum; i++)
parent[i] = 0;
for (i = 0; i < edgnum; i++)
{
n = Find(parent, edges[i].begin);
m = Find(parent, edges[i].end);
if (n != m)
{
parent[n] = m;//将此边结尾号放到起点为下标的parent数组中,表示已在生成树中,遍历会到此树最大标号的节点
printf("%3d--%3d,%3d
", edges[i].begin, edges[i].end, edges[i].weight);
}
}
}
7.测试函数
int main()
{
AdjMatrix myGraph,myweightG;
DataType s[6] = { 'A', 'B', 'C', 'D', 'E', 'F' };
DataType sweight[6] = { 'A', 'B', 'C', 'D', 'E', 'F' };
int arcs[][6] = {
{ 0, 1, 0, 1, 0, 1 },
{ 0, 0, 0, 0, 1, 0 },
{ 0, 0, 0, 0, 1, 1 },
{ 0, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0 },
{ 0, 0, 0, 0, 0, 0 } };
/*int arcs[][6] = { //此图是树
{ 0, 1, 0, 1, 0, 1 },
{ 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ 0, 0, 1, 0, 1, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0 } };*/
int arcsweight[][6] = {
{ 0, 6, 1, 5, un, un },
{ 6, 0, 5, un, 3, un },
{ 1, 5, 0, 5, 6, 4 },
{ 5, un, 5, 0, un, 2 },
{ un, 3, 6, un, 0, 6 },
{ un, un, 4, 2, 6, 0 } };
};
for (int i = 0; i < 6;i++)
myGraph.vertex[i] = s[i];
myGraph.vertexNum = 6;
myGraph.arcNum = 0;
for (int i = 0; i < myGraph.vertexNum;i++)
for (int j = 0; j < myGraph.vertexNum; j++)
{
myGraph.arc[i][j] = arcs[i][j];
if (myGraph.arc[i][j]==1)
myGraph.arcNum++;
}
for (int i = 0; i <6; i++)
myweightG.vertex[i] = sweight[i];
myweightG.vertexNum = 6;
myweightG.arcNum = 0;
for (int i = 0; i < myweightG.vertexNum; i++)
for (int j = 0; j < myweightG.vertexNum; j++)
{
myweightG.arc[i][j] = arcsweight[i][j];
if (myweightG.arc[i][j] != 0 && myweightG.arc[i][j]<un)
myweightG.arcNum++;
}
printf("广度优先遍历结果:
");
BFS_ADJTraverse(myGraph);
printf("
");
printf("深度优先遍历递归结果:
");
DFS_ADJTraverse(myGraph);
printf("
");
printf("深度优先遍历非递归结果:
");
DFS_ADJTraverseStack(myGraph);
printf("
");
if (IsTree(myGraph))
printf("
此图是树
");
else
printf("
此图不是树
");
printf("Prim算法生成树(弧尾--弧头,边权值):
");
MinTree_Prim(myweightG);
printf("
");
printf("Kruskal算法生成树(弧尾--弧头,边权值):
");
MinTree_Kruskal(myweightG);
printf("
");
system("pause");
return 0;
}
8.测试结果
