
反向思维:如果知道最小值,那如何求出这个最小值所在的子数组, 即找到这个最小值左边比它更小的元素的位置left 和 右边比它更小的元素的位置right,res += A[i] * ( i - left ) * ( right - i )。
class Solution { public: int sumSubarrayMins(vector<int>& A) { // find one element : right : next smaller element, left : smaller/equal element int n = A.size(); vector<int> preSmaller(n, -1); //preSmaller[i] = j : i的前面第一个比i小的元素的位置j vector<int> nextSmaller(n, n); //nextSmaller[i] = j : i的后面第一个比i小的元素的位置j //单调栈:(非严格)增序,存index stack<int> Stack; //找nextSmaller for(int i=0; i<n; i++){ while(!Stack.empty() && A[Stack.top()] > A[i]){ //遇到一个比栈顶元素小的,退栈 nextSmaller[Stack.top()] = i; Stack.pop(); } Stack.push(i); } while(!Stack.empty()) Stack.pop(); //把栈清空 //找preSmaller //注意做记录的位置和之前的不同 for(int i=0; i<n; i++){ while(!Stack.empty() && A[Stack.top()] > A[i]) //栈顶元素大于A[i]时,退栈 Stack.pop(); if(!Stack.empty()) preSmaller[i] = Stack.top(); Stack.push(i); } long result = 0; long M = 1e9+7; for(int i = 0; i<n; i++){ //以A[i]为最小元素的subarray个数 long times = (i-preSmaller[i])*(nextSmaller[i] - i); result += A[i] * times; result %= M; } return result; } };

解法一:记忆化递归:
class Solution { public: vector<long> sums; vector<vector<int>> mem; int splitArray(vector<int>& nums, int m) { //记忆化递归 int n = nums.size(); sums = vector<long>(n); mem = vector<vector<int>>(m+1, vector<int>(n, INT_MAX)); //将个数为n得数组分成m个非空连续子数组 sums[0] = nums[0]; for(int i=1; i<n; i++){ sums[i] = sums[i-1] + nums[i]; // 前序和 } return splitArray(nums, n-1, m); } int splitArray(vector<int>& nums, int k, int m){ //min of largest sum of splitting nums[0] - nums[k] into m groups if(m==1) //划分为1个数组 return sums[k]; if(m > k+1) return INT_MAX; if(mem[m][k] != INT_MAX) return mem[m][k]; int ans = INT_MAX; for(int i=0; i<k; i++) ans = min(ans, max(splitArray(nums, i, m-1), int(sums[k]-sums[i])) ); return mem[m][k] = ans; } };
解法二:动态规划
class Solution { public: int splitArray(vector<int>& nums, int m) { int n = nums.size(); vector<long> sums(n); vector<vector<int>> dp(m+1, vector<int>(n, INT_MAX)); //前缀和 sums[0] = nums[0]; for(int i=1; i<n; i++){ sums[i] = sums[i-1] + nums[i]; } //将0-i个数分为1组就是其前缀和 for(int i=0; i<n; i++){ dp[1][i] = sums[i]; } // dp[i][j]:把nums[0] - nums[j] 分为i组 for(int i=2; i<=m; i++){ //将数组划分为i组 for(int j=i-1; j<n; j++){ //末尾元素位置为j for(int k=0; k<j; k++){ //起始元素位置为k // 将0-j分为i组的问题 转化为 将0-k分为i-1组的问题 + sum(k+1...j) dp[i][j] = min(dp[i][j], max(dp[i-1][k], int(sums[j]-sums[k]) ) ); } } } return dp[m][n-1]; } };
解法三:二分法
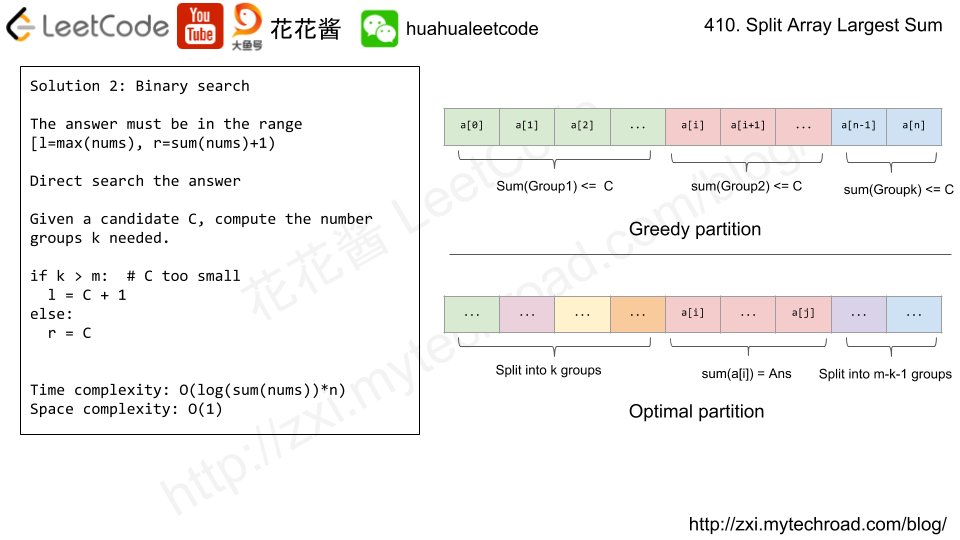

l = max(nums) : 将nums中的每个元素分为1组中的最大值 为 range的下界;
r = sum(nums) : 将nums整体分为1组为range的上界;
range为左闭右开区间,所以 r+1
问题转化为=> 找到一个最小的candidate C ,使得将nums划分为m组的每一组都不大于C
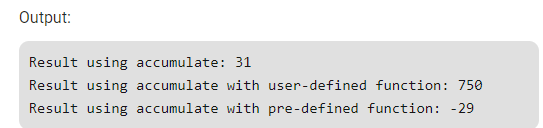
accumulate()
This function returns the sum of all the values lying in a range between [first, last) with the variable sum.
- Syntax 1:
accumulate(first, last, sum); first, last : first and last elements of range whose elements are to be added sum : initial value of the sum - Syntax 2: This function returns the sum of all the values lying between [first, last) with the variable sum.
accumulate(first, last, sum, myfun); myfun : a function for performing any specific task. For example, we can find product of elements between first and last.
// C++ program to demonstrate working of accumulate() #include <iostream> #include <numeric> using namespace std; // User defined function int myfun(int x, int y) { // for this example we have taken product // of adjacent numbers return x * y ; } int main() { // Initialize sum = 1 int sum = 1; int a[] = {5 , 10 , 15} ; // Simple default accumulate function cout << " Result using accumulate: "; cout << accumulate(a , a+3 , sum); // Using accumulate function with // defined function cout << " Result using accumulate with" "user-defined function: "; cout << accumulate(a, a+3, sum, myfun); // Using accumulate function with // pre-defined function cout << " Result using accumulate with " "pre-defined function: "; cout << accumulate(a, a+3, sum, std::minus<int>()); return 0; }
class Solution { public: int splitArray(vector<int>& nums, int m) { long l = *max_element(begin(nums), end(nums)); //得到nums中的最大值 //统计nums中元素的和 并加1 long r = accumulate(begin(nums), end(nums), 0L) +1; // 0L表示long型的0 while(l<r){ long limit = l + (r-l)/2; if(min_groups(nums, limit) > m) //子数组的数量超过m,将每个子数组的和:candidate C分配的大一点 l = limit+1; else r = limit; } return l; } int min_groups(vector<int>& nums, long limit){ long sum = 0; //子数组中元素的和 int groups = 1; //子数组的数量 for(int num : nums){ if(sum + num > limit){ sum = num; groups ++; } else sum += num; } return groups; } };
约瑟夫环问题:

参考:剑值offer 面试题62
解法一:链表
class Solution { public: int LastRemaining_Solution(int n, int m) { if(n<1 || m<1) return -1; int i=0; list<int> numbers; //用std::list来模拟一个环形链表 for(i=0; i<n; i++) numbers.push_back(i); list<int>::iterator current = numbers.begin(); while(numbers.size() >1){ for(int i=1; i<m; i++){ current ++; if(current == numbers.end()) current = numbers.begin(); //因为list不是一个环形结构,故每当current扫描到链表末尾时就将其移到头部 } //list<int>::iterator next = ++current; current++; //current加1后指向被杀掉的人的下一个人 list<int>::iterator next = current; if(next == numbers.end()) next = numbers.begin(); current--; //current-1 后指向被杀掉的人 numbers.erase(current); current = next; } return *current; } };
解法二:循环/递归,用数学找规律法找到一个递归式:


循环写法:
class Solution { public: int LastRemaining_Solution(int n, int m) { if(n<1 || m<1) return -1; int last = 0; for(int i=2; i<=n; i++){ last = (last+m)%i; } return last; } };
hulu 2019笔试第一题:

-
通过约瑟夫环找到由第一个节点开始时获胜的节点的index
-
归纳总结得到 第i个节点开始时获胜的节点为(i+index)%array_len
-
线性获得权值
// pch.cpp: 与预编译标头对应的源文件;编译成功所必需的 #include "pch.h" // 一般情况下,忽略此文件,但如果你使用的是预编译标头,请保留它。 #include <vector> #include <list> #include <map> #include <set> #include <queue> #include <deque> #include <stack> #include <bitset> #include <algorithm> #include <functional> #include <numeric> #include <utility> #include <sstream> #include <iostream> #include <iomanip> #include <cstdio> #include <cmath> #include <cstdlib> #include <ctime> #include <string> #include <cstring> #include <math.h> using namespace std; int yuesefu(int N, int M) { if (N == 1) { return 0; //这里返回下标,从0开始,只有一个元素就是剩余的元素0 } else { return (yuesefu(N - 1, M) + M) % N; //我们传入的n是总共多少个数 } } int main() { int n, m; cin >> n >> m; vector<int> a(n); vector<int> w(n); vector<double> v(n); for (int i = 0; i < n; i++) { cin >> a[i]; //1 good ; 0 bad } double sum = 0; for (int i = 0; i < n; i++) { cin >> w[i]; //1 good ; 0 bad sum += w[i]; } for (int i = 0; i < n; i++) { v[i] = w[i] / sum; } double x = 0; int r = yuesefu(n, m); if(a[r] == 1) x += v[0]; for (int i = 1; i < n; i++) { if (a[(i + r) % n] == 1) x += v[i]; } cout << setiosflags(ios::fixed) << setprecision(5) << x << endl; return 0; }