二叉树 + 递归 + 分治法 + BFS 总结 leetcode: 前序中序后序的的递归及非递归遍历；二叉树的最近公共祖先

二叉树递归相关题目的时间复杂度基本上都是O(n) = 一共有n个点 + 每个点的时间复杂度(1)

而二叉树分治法最坏的时间复杂度为O(n^2)

时间复杂度：T(n) = 2T(n/2) + O(1) = O(n)

Merge Sort, Quick Sort: T(n) = 2T(n/2) + O(n) = O(nlogn)

前序遍历：

解法一：递归，通常是设置一个全局变量来保存结果。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traverse(root, result);
        return result;
    }
    void traverse(TreeNode* root, vector<int>& res){
        //递归终止条件
        if(root == NULL)
            return;
        res.push_back(root->val);
        traverse(root->left, res);
        traverse(root->right, res);
    }
};

解法二：Divide & Conquer

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root == NULL)
            return res;
        
        //divide
        vector<int> left = preorderTraversal(root->left);
        vector<int> right = preorderTraversal(root->right);
        
        //conquer
        res.push_back(root->val);
        for(auto i : left)
            res.push_back(i);
        for(auto i : right)
            res.push_back(i);
        return res;
    }
};

解法三：非递归版本C++

采用堆栈实现。

根节点先入栈
判断栈是否为空，飞空则出栈并加入结果队列
先把右子树入栈再把左子树入栈，这样出栈的时候是先左后右，（中间根已经在上一步输出）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root == NULL)
            return res;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()){
            TreeNode* node = st.top();
            st.pop();
            res.push_back(node->val);
            if(node->right)
                st.push(node->right);
            if(node->left)
                st.push(node->left);
        }
        return res;
    }
};

中序遍历：

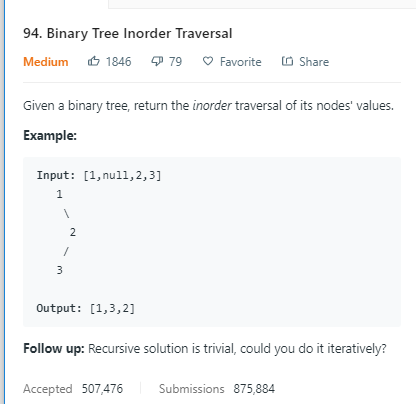
一. 递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root == NULL)
            return res;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()){
            TreeNode* node = st.top();
            st.pop();
            res.push_back(node->val);
            if(node->right)
                st.push(node->right);
            if(node->left)
                st.push(node->left);
        }
        return res;
    }
};

二. Divide and Quaqer

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root == NULL)
            return res;
        
        vector<int> left = inorderTraversal(root->left);
        vector<int> right = inorderTraversal(root->right);
        
        for(int i : left)
            res.push_back(i);
        res.push_back(root->val);
        for(int i: right)
            res.push_back(i);
        
        return res;
    }
};

三. 非递归，用栈来实现。

栈或者当前结点不为空时：

1）把当前结点压入栈中，然后继续压入它的左结点，直到左结点为空；

2）将栈顶元素的值保存在res中，并弹出；

3）转到右结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode* > st;
        TreeNode* cur = root;
        while(cur || !st.empty()){
            while(cur){
                st.push(cur);
                cur = cur->left;
            }
            cur = st.top();
            st.pop();
            res.push_back(cur->val);
            cur = cur->right;
        }
        return res;
    }
};

后序遍历：

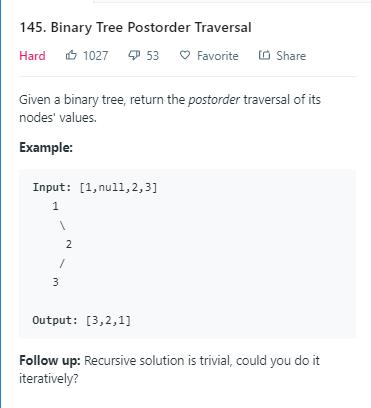
一.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        traverse(root, res);
        return res;
    }
    void traverse(TreeNode* root, vector<int>& res){
        if(root == NULL)
            return;
        traverse(root->left, res);
        traverse(root->right, res);
        res.push_back(root->val);
    }
};

二.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root == NULL)
            return res;
       
        vector<int> left = postorderTraversal(root->left);
        vector<int> right = postorderTraversal(root->right);
        
        for(int i: left)
            res.push_back(i);
        for(int i: right)
            res.push_back(i);
        res.push_back(root->val);
        
        return res;
    }
};

三.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode* > st;
        if(root == NULL)
            return res;
        st.push(root);
        while(!st.empty()){
            TreeNode* tmp = st.top();
            st.pop();
            res.insert(res.begin(), tmp->val);   //在前端插入
            if(tmp->left)
                st.push(tmp->left);
            if(tmp->right)
                st.push(tmp->right);
        }
        return res;
    }
};

一.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    int dep_max;    //全局变量
public:
    int maxDepth(TreeNode* root) {
        dep_max = 0;
        helper(root, 1);  //1为当前根结点
        return dep_max;  
         
    }
    void helper(TreeNode* root, int depth){
        if(root==NULL) return;
        
        dep_max = max(dep_max, depth);
        helper(root->left, depth+1);
        helper(root->right, depth+1);
    }
};

二.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==NULL) return 0;
        
        //左右子树的深度
        int left = maxDepth(root->left);
        int right = maxDepth(root->right);

        return max(left, right)+1;  
         
    }

    
};

平衡二叉树：左右子树高度相差不超过1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root==NULL)
            return true;
        if(abs(getDepth(root->left) - getDepth(root->right)) > 1)
            return false;
        return isBalanced(root->left) && isBalanced(root->right);
    }
    int getDepth(TreeNode* root){
        if(!root)
            return 0;
        return max(getDepth(root->left), getDepth(root->right)) + 1;
    }
    
};

上面的方法使得每个结点都会被上面的点计算深度时访问一次，优化一下：若发现某个结点的子树不平衡，则不计算它的深度，直接返回-1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(depth(root) == -1)
            return false;
        return true;
    }
    int depth(TreeNode* root){
        if(!root)
            return 0;
        int left = depth(root->left);
        if(left==-1)
            return -1;
        int right = depth(root->right);
        if(right == -1)
            return -1;
        int dif = abs(left - right);
        if(dif>1)
            return -1;
        else
            return max(left, right)+1;
    }
};

二叉搜索树的性质是：左子树的值 < 根节点 < 右子树的值

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {        
        if(p->val > q->val)
            swap(p,q);   // ensure p < q
        
        while(root){
            if(root->val < p->val)
                root = root->right;
            else if(root->val > q->val)
                root = root->left;
            else
                return root;
        }
        return NULL;
    }
};

已知A和B的父亲结点：

思路：把A和A的父结点保存在set中，若在B及B的父结点中找到一个和set中相同的结点，就返回这个公共祖先。

/**
 * Definition of ParentTreeNode:
 * class ParentTreeNode {
 * public:
 *     int val;
 *     ParentTreeNode *parent, *left, *right;
 * }
 */


class Solution {
public:
    /*
     * @param root: The root of the tree
     * @param A: node in the tree
     * @param B: node in the tree
     * @return: The lowest common ancestor of A and B
     */
    ParentTreeNode * lowestCommonAncestorII(ParentTreeNode * root, ParentTreeNode * A, ParentTreeNode * B) {
        // write your code here
        if(root == NULL)
            return NULL;
            
        unordered_set<ParentTreeNode*> s;  //保存A向上的路径
        while(A!=NULL){
            s.insert(A);
            A = A->parent;
        }
        
        while(B){
            if(s.find(B) == s.end())
                //s中找不到相同的结点
                B = B->parent;
            else
                return B;
        }
        
    }
};

未知p，q的父亲结点：

分治法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
//若找到了LCA，就返回LCA，即 p和q出现在一左一右，返回它的根结点
//若只找到n1， 就返回n1
//若只找到了n2, 就返回n2
//若都不存在，返回NULL
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL)
            return NULL;
        if(root == p || root == q)
            return root;
        
        //divide
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        
        //Conquer
        if(left != NULL && right != NULL)
            return root;
        
        if(left != NULL)
            return left;
        
        if(right != NULL)
            return right;
        
        return NULL;
    }
};

递归：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL || root == p || root == q){
            return root;
        }
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        if(left && right) return root;
        if(left && right == NULL) return left;
        if(right && left == NULL) return right;
        return NULL;
    }
};

从任一结点到任一结点路径的最大值：

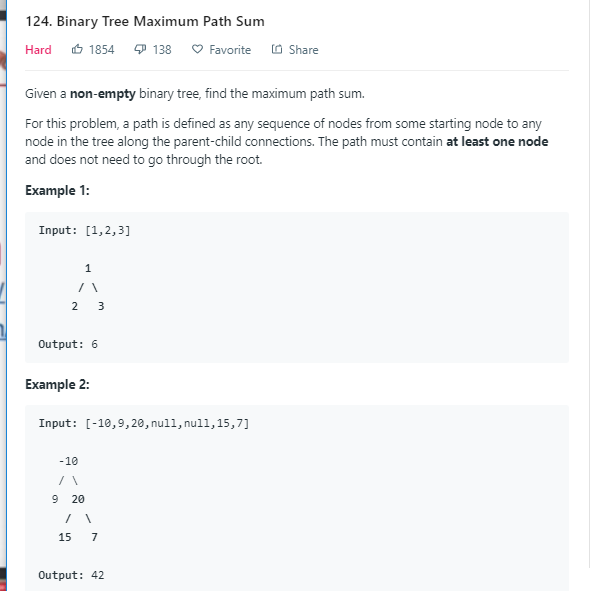
参考链接：https://www.geeksforgeeks.org/find-maximum-path-sum-in-a-binary-tree/

/**
 * Definition of TreeNode:
 * class TreeNode {
 * public:
 *     int val;
 *     TreeNode *left, *right;
 *     TreeNode(int val) {
 *         this->val = val;
 *         this->left = this->right = NULL;
 *     }
 * }
 */
//一颗二叉树，求从根结点到叶子结点的路径的最大值；求从根结点到任一结点的路径的最大值
class Solution {
public:
    /**
     * @param root: The root of binary tree.
     * @return: An integer
     */
    int maxPathSum(TreeNode * root) {
        // write your code here
        if (root == NULL)
            return 0;
        int left = maxPathSum(root->left);
        int right = maxPathSum(root->right);

        //root -> leaf
        //return max(left, right) + root->val;

        //root-> anynode
        return max(0, max(left, right)) + root->val;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
//any to any node: 最长路径的位置：完全在左边；完全在右边；跨过根结点
 //O(n)
class Solution {
public:
    int findMax(TreeNode* root, int &res){
        if(root == NULL)
            return 0;
        
        int l = findMax(root->left, res);
        int r = findMax(root->right, res);
        
        int max_single = max(max(l, r)+root->val, root->val);
        int max_round = max(max_single, l+r+root->val);
        
        res = max(res, max_round);   //store the maximum result
        return max_single;
    }
    
    int maxPathSum(TreeNode* root) {
        int res = INT_MIN;
        findMax(root, res);
        return res;
    }
};

//这次完全是自己写出来的噢

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxd;

    int dfs(TreeNode* cur){
        if(cur == NULL) return 0;

        int left = dfs(cur->left);
        int right = dfs(cur->right);
        int d = cur->val;
        if(left > 0) d+= left;
        if(right > 0) d+= right;
        maxd = max(maxd, d);
        int recur_d = cur->val;
        if(left>0 || right>0){
            recur_d += left>right ? left : right;
        }
        return recur_d;
    }


    int maxPathSum(TreeNode* root) {
        maxd = -1e9;
        dfs(root);
        return maxd;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;
        if(root == NULL)
            return res;   //返回空vector res
        
        if(root->left==NULL && root->right==NULL)
            res.push_back(to_string(root->val));
        
        //divide
        vector<string> left = binaryTreePaths(root->left);
        vector<string> right = binaryTreePaths(root->right);
        
        //conquer
        for(string s : left)
            res.push_back(to_string(root->val) + "->" + s);
        for(string s : right)
            res.push_back(to_string(root->val) + "->" + s);
        
        return res;
        
    }
};

注意这里s不能传入引用。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<string> res;

    void dfs(TreeNode* cur, string s){
        if(cur == NULL) return;

        s += (to_string(cur->val));

        if(cur->left == NULL && cur->right == NULL){
            res.push_back(s);
        }

        if(cur->left) dfs(cur->left, s + "->");
        if(cur->right) dfs(cur->right, s + "->");

    }

    vector<string> binaryTreePaths(TreeNode* root) {
        res={};
        if(root == NULL) return res;

        string s = "";
        dfs(root, s);
        
        return res;
    }
};

用队列来实现二叉树的宽度优先搜索：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
//BFS + queue
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode* > q;
        vector<vector<int>> res;
        if(root == NULL)
            return res;
        
        q.push(root);
        while(!q.empty()){
            int size = q.size();  //取每一层有多少结点，一定要取出来，因为q.size()会变化
            vector<int> curlevel;
            //遍历每一层
            for(int i=0; i<size; i++){
                TreeNode* tmp = q.front();
                curlevel.push_back(tmp->val);
                q.pop();
                if(tmp->left != NULL)
                    q.push(tmp->left);
                if(tmp->right != NULL)
                    q.push(tmp->right);
                
            }
            res.push_back(curlevel);
        }
        
        return res;
    }
};

448. Inorder Successor in BST

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */


class Solution {
public:
    /*
     * @param root: The root of the BST.
     * @param p: You need find the successor node of p.
     * @return: Successor of p.
     */
    TreeNode* cur = NULL;
    TreeNode * inorderSuccessor(TreeNode * root, TreeNode * p) {
        // write your code here
        if(root == NULL || p == NULL) return NULL;
        
        if(root->val <= p->val){
            if(root->right){
                inorderSuccessor(root->right, p);
            }
        }
        else{
            if(root->left) cur = inorderSuccessor(root->left, p);
            if(cur == NULL) return root;
            else return cur;
        }
        
    }
};

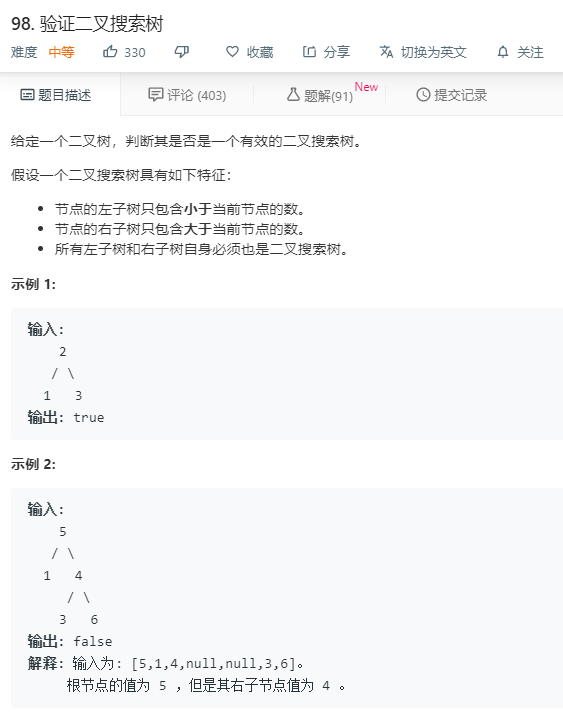
1）

参考： https://zhuanlan.zhihu.com/p/46841937

/** 
 * Definition for a binary tree node. 
 * struct TreeNode { 
 *     int val; 
 *     TreeNode *left; 
 *     TreeNode *right; 
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {} 
 * }; 
 */  
class Solution {  
public:  
    bool isValidBST(TreeNode* root) {  
          
        if(root == NULL) return true;  
        if(root->left == NULL && root->right == NULL) return true;  
        if(root->left){  
            TreeNode* leftmax = left_Max(root->left);  
            if(root->val <= leftmax->val)  
                return false;  
        }  
        if(root->right){  
            TreeNode* rightmin = right_Min(root->right);  
            if(root->val >= rightmin->val)  
                return false;  
        }  
        return isValidBST(root->left) && isValidBST(root->right);  
    }  
    TreeNode* left_Max(TreeNode* cur){  
        while(cur->right)  
            cur = cur->right;  
        return cur;  
    }  
    TreeNode* right_Min(TreeNode* cur){  
        while(cur->left)  
            cur = cur->left;  
        return cur;  
    }  
};

2）中序遍历这颗BST，将结点存到数组res中，再判断res中的结点是否是严格递增的

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> res;

    void inOrder(TreeNode* cur){
        if(cur == NULL) return;
        inOrder(cur->left);
        res.push_back(cur->val);
        inOrder(cur->right);
    }

    bool isValidBST(TreeNode* root) {
        if(root == NULL) return true;
        
        inOrder(root);

        for(int i=0; i<res.size()-1; i++){
            if(res[i] >= res[i+1])
                return false;
        }

        return true;
    }
};

相关阅读:
【Java学习】01. Java基本介绍及环境搭建
 vue组件之间的传值
 检测上传的文件类型js实现方式
 正则表达式学习笔记
 Nuxt.js学习笔记
 Vue+typescript+vuex项目实践学习笔记
 项目依赖&开发依赖
 vuex学习笔记
 export与export default的区别
 ES6 数组去重方法
原文地址：https://www.cnblogs.com/Bella2017/p/11384471.html

二叉树 + 递归 + 分治法 + BFS 总结 leetcode: 前序 中序 后序的的递归及非递归遍历；二叉树的最近公共祖先

二叉树 + 递归 + 分治法 + BFS 总结 leetcode: 前序中序后序的的递归及非递归遍历；二叉树的最近公共祖先