class Solution { public: int findPaths(int m, int n, int N, int i, int j) { int M = 1e9 +7; if(N==0)return 0; int dp[m][n] = {0}; int dp2[m][n]; for(int k=0; k<m; ++k) for(int t=0; t<n; ++t) dp[k][t]=(k==0)+(k==m-1)+(t==0)+(t==n-1); int ans = dp[i][j]; for(int p=0; p<N-1; ++p){ for(int k=0; k<m; ++k){ for(int t=0; t<n; ++t){ int a = (k>0?dp[k-1][t]:0)% M; int b = (k<m-1?dp[k+1][t]:0) % M; int c = (t>0?dp[k][t-1]:0) % M; int d = (t<n-1?dp[k][t+1]:0) % M; dp2[k][t] = ((a+b)%M+(c+d)%M)%M; //if(k==i && t==j) //ans = (ans + dp2[k][t])%M; } } ans = (ans + dp2[i][j]%M)%M; memcpy(dp, dp2, m*n*sizeof(int)); } return ans; } };

思路:
1) 首先计算数组nums里数的和,设为sum;
2)设置一维vector数组dp,长度为 2*sum+1,即下标从0到2*sum,实际表示[-sum, sum]范围内和为索引的有多少种方式。
3)设置一维vector数组d,长度为 2*sum+1,储存每次遍历dp后的值,再覆盖dp。
注意:
1) 将一个vector赋值给另一个vector的语句:dp.assign(d.begin(), d.end());
2)将vector里的值都赋值为0的语句:fill(d.begin(), d.end(), 0);
3)边界条件:sum<S 时 返回 0
4)初始化:用+nums[0],-nums[0] 来初始化dp;
5)遍历中,dp不是累加1,而是累加上上一次的值。
class Solution { public: int findTargetSumWays(vector<int>& nums, int S) { int n = nums.size(); if(n==0 && S==0) return 1; int sum = 0; for(int i=0; i<n;++i){ sum += nums[i]; } if(sum<S) return 0; vector<int> dp(2*sum+1, 0); vector<int> d(2*sum+1, 0); dp[sum + nums[0]] += 1; dp[sum - nums[0]] += 1; for(int i=1; i<n; i++){ for(int j=0; j<2*sum+1; j++){ if(dp[j]!=0){ d[j+nums[i]] += dp[j]; d[j-nums[i]] += dp[j]; } } dp.assign(d.begin(), d.end()); fill(d.begin(), d.end(), 0); } return dp[sum + S]; } };
vector中的sort排序:
vector<int>v;
-
sort(v.begin(), v.end(),less<int>());//升序(默认)也可写为:sort(v.begin(), v.end());
sort(v.begin(), v.end(),greater<int>());//降序
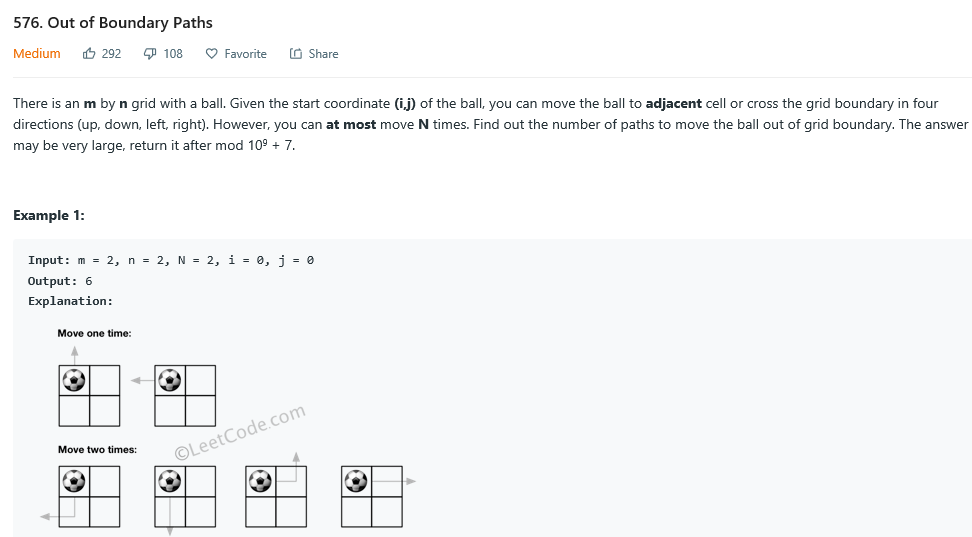
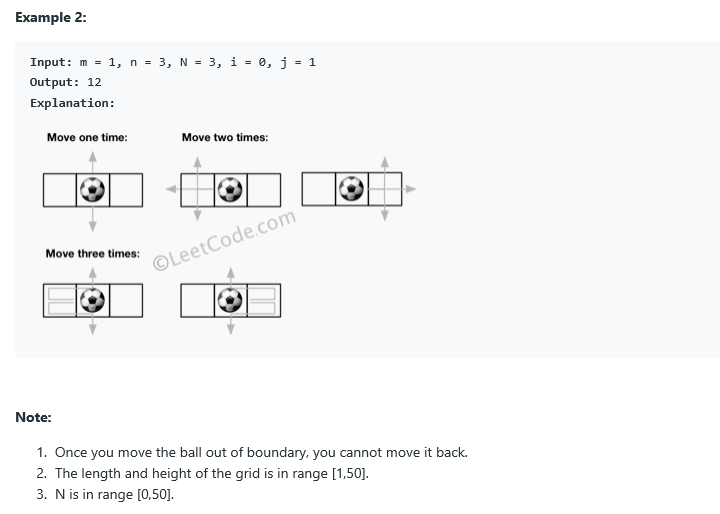
思路:首先初始化一个二维dp[k][t] 矩阵,用来保存需要n步(n<N)走出边界。初始化:当k==0 || k==m-1 || t==0 || t==n-1 时都可以一步走出去。
然后循环N次,更新dp矩阵为上下左右的元素相加。设置ans来记录(i,j)位置每次循环的和。