T1.小 Z 切课本(cut)
小 Z 厌恶数学,他决定将数学课本切成一块一块的。他的课本是一个 n*m 的
矩形,小 Z 决定切 K 刀,每刀他可以横着切或者竖着切,但是切成的矩形的长和
宽都必须是整数。当然,小 Z 不会做出两次相同的操作。例如 n=6,m=4,k=3 时,
以下是一种合法的切法。
不巧的是,小 Z 的数学老师知道了他这个行为,并且刁钻的老师肯定会找到
切出的矩形中面积最小的那一块来 D 他, 所以小 Z 想知道最优情况下面积最小
的那一块面积最大能是多少?
[输入格式]
从 cut.in 中读取数据。
输入数据只包含一行三个整数 n,m,k,含义如题目所述。
[输出格式]
输出一个数字,表示答案。 如果没有合法的方案,输出-1。
[样例输入]
6 4 2
[样例输出]
8
[数据范围与约定]
本题采用子任务制,你只有通过一个 subtask 下的所有测试点才能得到对应的分
数。
Subtask1 : 包含 20Points 满足 n,m<=10
Subtask2 : 包含 20Points 满足 n,m<=5000
Subtask3 : 包含 20Points 满足 n,m<=10^7
Subtask4 : 包含 40Points 满足 n,m<=10^9
对于所有数据,满足 n,m,k>=1, k<=10^9
题解:①无解:k<n+m-2;②k<n或k<m:最优解必定是沿一个方向切,2个方向取最小值即可;③k>m且k>n:我们把一边切满,然后另一边就转换成第二种情况啦,平均切即可,2种情况取最小值。
代码如下:
1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 int n,m,k; 5 long long ans1,ans2; 6 int main() 7 { 8 freopen("cut.in","r",stdin); 9 freopen("cut.out","w",stdout); 10 scanf("%d%d%d",&n,&m,&k); 11 if(k>n+m-2){printf("-1");return 0;} 12 if(n>=k+1||m>=k+1){ 13 ans1=n/(k+1); ans2=m/(k+1); 14 printf("%lld",max(ans1*m,ans2*n)); 15 return 0; 16 } 17 int k1=k-n+1,k2=k-m+1; 18 ans1=m/(k1+1),ans2=n/(k2+1); 19 printf("%lld",max(ans1,ans2)); 20 return 0; 21 }
T2.海棠数组(array)
小 Z 最喜欢数组了,现在他得到了由 n 个正整数组成的数组 ai,他想构造
一个相同大小的正整数数组 bi 满足两个数组的差异度∑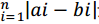 最小。
最小。
特殊的是, bi 数组的所有元素必须满足两两互质。
[输入格式]
从 array.in 中读取数据。
第一行一个数 n, 表示数组大小。
接下来一行 n 个正整数 ai, 表示给定的数组。
[输出格式]
输出一行 n 个正整数 bi,表示答案。
输出的数字必须满足 1<=bi<=10^9。如果有多个答案,你可以输出任意一个。
[样例输入]
5
1 6 4 2 8
[样例输出]
1 5 4 1 9
[样例解释]
差异度为 3,可以证明是最小的差异度。还有其它可行的方案。
[数据范围与约定]
本题采用子任务制,你只有通过一个子任务所有的数据才能得到对应的分数。
Subtask1:包含 20Points,满足 n<=8 1<=ai<=5
Subtask2:包含 30Points,满足 n<=50 1<=ai<=15
Subtask3:包含 50Points,满足 n<=100 1<=ai<=30
题解:状压dp
T3.小 Z 爱修路(road)
L 国包含 n 个城市和 m 条双向道路,第 i 条道路连接 ui,vi 两个城市, 距离为
ti,这些道路将所有 n 个城市连接在一起。 明年, L 国将会在首都,也就是 1 号
城市举办一年一度的 noi,所以 L 国的国王委托小 Z 新建一些道路来减少一些城
市到达首都的距离。小 Z 很快修好了道路,但是他却不是很满意。他想知道最多
可以少新建多少道路,满足首都到所有城市的最短路长度和现在相同。
[输入格式]
从 road.in 中读取数据。
第一行读入三个数字 n,m,k,依次表示城市的数量,原有道路的数量和新建道路
的数量。
接下来 m 行,每行三个数字 ui,vi,ti,表示一条原有的道路
最后 k 行,每行两个数字 si,wi,表示一条新建的道路连接 1 和 si,距离为 wi。
[输出格式]
输出一个整数,表示最多能少修建多少条新建的道路。
[样例输入]
3 2 2
1 2 1
2 3 1
2 2
3 1
[样例输出]
1
[数据范围与约定]
对于 20%的数据,满足 n,m,k<=100
对于另外 20%的数据,满足 k<=4
对于 100%的数据,满足 n,k<=50000 , m<=200000 , 1<=ti,wi<=10^9 , si>=2