【组合数学】【恒等式】(C_{n}^{r} imes C_{n-r}^{k-r}=C_{n}^{k} imes C_k^{r})
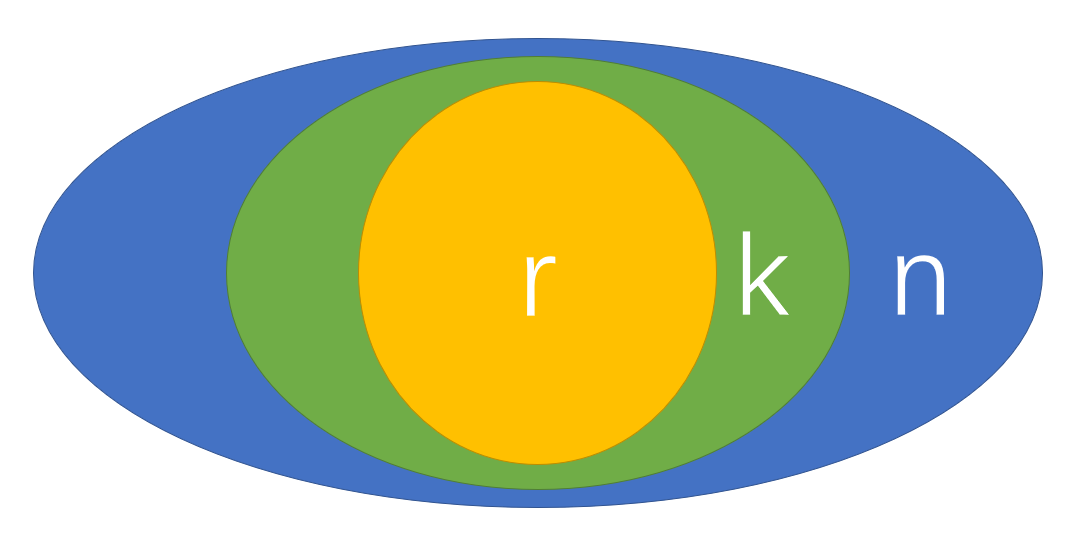
假设有这么一个场景,有n个人参加了一次抽奖活动,其中有k个人获奖,而在这k个人之中又有r个人获得了一等奖,假设每个人中奖的概率是均匀的,求问一共会出现多少种不同的中奖的情况?
思路一:
第一步先从n个人中挑出k个人作为中奖者,然后再继续从k个人之中挑出r个人作为获得一等奖的人选,于是有(C_n^k imes C_k^r)。
思路二:
不同于思路一,我们可以先从n个人直接先挑出r个人作为我们一等奖的人选,再从剩余的n-r个人中挑出k-r个人作为其他获奖的人选。
由于这两种思路都是用于计算同一个问题,所以通过这两种方法算出的答案应是相同的。