前言
本博客将分析OO新手fry第一单元的三次作业,以及和bug斗争的心路历程......
第一次作业
程序结构分析
UML类图
程序讲解
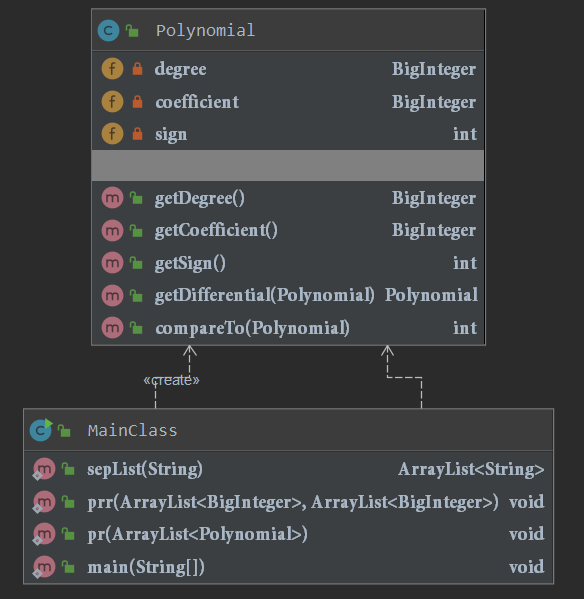
本次作业并不是很复杂,本人所采用的结构也比较简单。程序包括两个类,一个是Polynomial类表示项,一个是Main类用于解析输入以及建立项的对象。
其中Polynomial类有degree(表示指数的幂次),coefficient(表示项的系数),sign(表示项的符号)这三个private属性,并分别通过getDegree(),getCoefficient(),getSign()的三个方法进行他类调用。对于关键的求导步骤,本人在Polynomial类中建立了getDifferential()方法,返回一个Polynomial类型的对象,为后续的排序做准备,重写了compareTo方法。
mainClass类则负责解析输入,建立对象和输出。设立了分割方法,打印方法,和总的main方法,这些方法都没有什么特别的,不在此详细说明。
结构分析
第一次作业当时感觉比较容易,设计性不是很强,也没有为之后的作业考虑,这样一锅粥的写法颇有当年C语言一main到底的赶脚,写的挺快,完全没有意识到之后作业的凶残,用一位朋友的话评价就是:这很不OO....
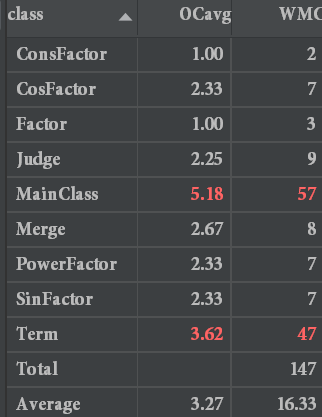
耦合度分析
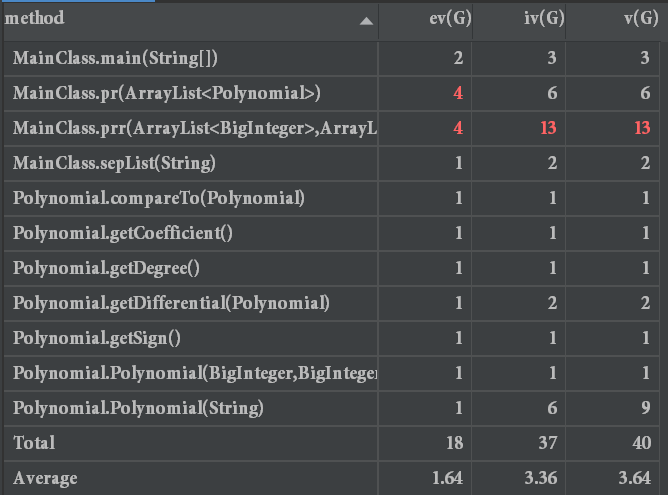
由于写的很不OO,这次代码的耦合度较高,整个解析过程直接在一个函数里完事,输出过程也没想到重写toString方法,而是写了一个单独的输出函数(在代码风格检查时由于方法行数超过了60,不得已分成了两个方法),坦言之,这是一个为了过测试点而存在的程序,代码的复用性几乎为0.
bug分析
个人bug
由于本人在处理合并后为0的式子处理的实在是太过于啰嗦,输出又是一个单独的函数,没有形成字符串而是直接输出,导致会出现合并结果为0而没有输出的神必情况。而在我绞尽脑汁枚举所有可能为0的情况进行输出时,最后还是漏了一个。在不那么强测中侥幸生存,在互测中被朋友们发现了bug,最后修复。这也是我的设计方法的缺陷,如果输出可以提前用字符串的到,那么对于没有空字符串加一个特判输出0即可,比一一枚举省力且正确性高。没事,吃一堑长一智,咱下次作业就用。
别人bug
在互测过程中,发现了两类bug。一类是输出格式不正确(1x出现了!),还有一类是正负号解析出了错。由于这次作业较为简单,评测机跑不出来太多的bug,跑出来的还都是同质的基本上,因此,还是要手动构造一些数据去hack。
第二次作业
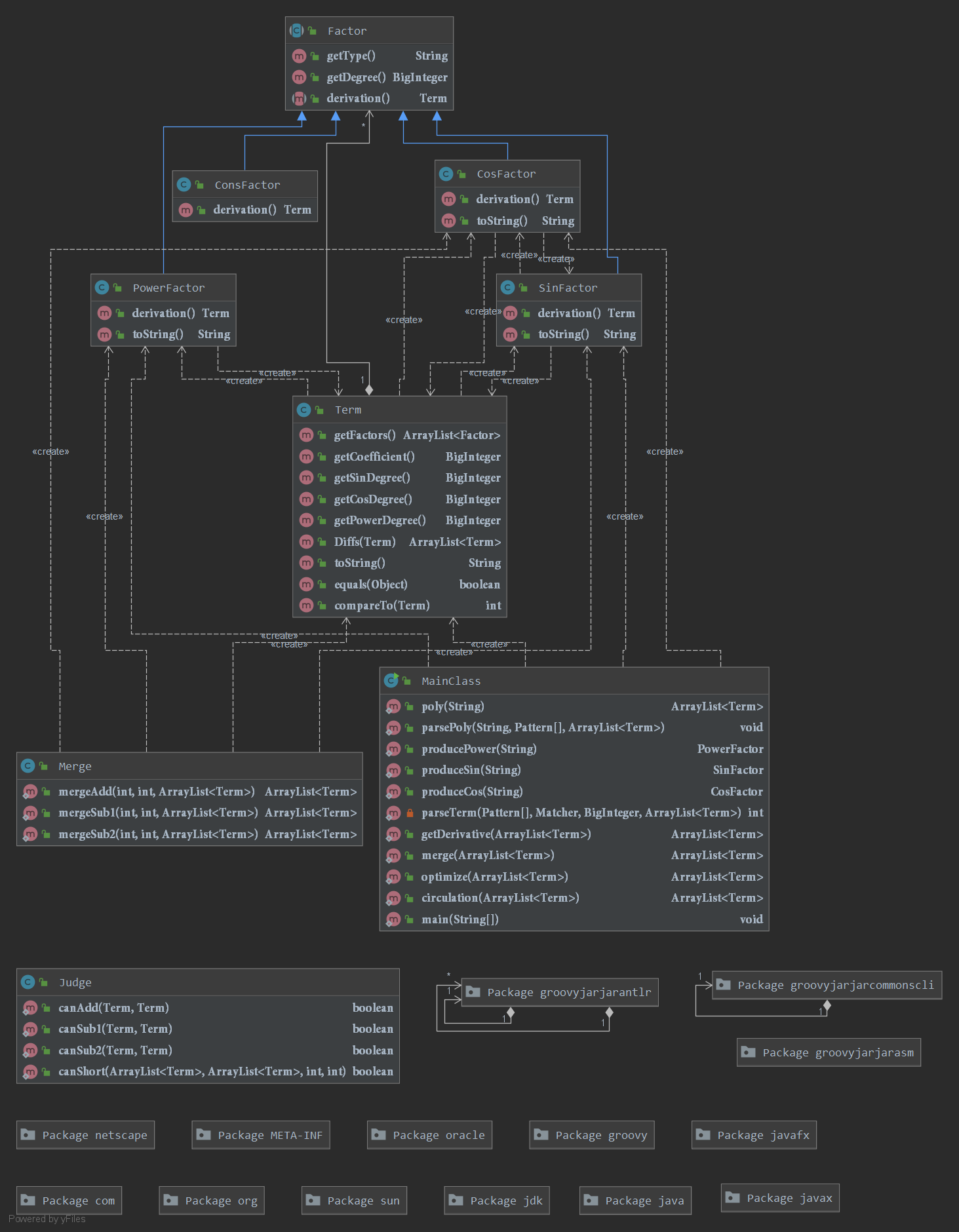
程序结构分析
UML类图
程序讲解
本次作业加入了三角函数以及格式判断。思路是解析字符串--->创建对象--->求导--->优化--->输出。
由于第一次作业写的过于草率,第二次不得不大规模重构。首先,我创建了因子抽象类(Factor),具有幂次和类型两个属性;之后,创建三角函数类(SinFactor,CosFactor),幂函数因子(PowerFactor),常数因子(ConsFactor)这几类分别继承Factor,之后再创建Term类(项),由于求导等操作。
之后为了优化,我又加入了判断类(主要用于判断三角函数能否进行合并),合并类(用于合并三角函数)。
在主类解析,创建对象,求导,优化。(这样看来还是非常面向过程,但比第一次有了进步)
耦合度分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| ConsFactor.ConsFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| ConsFactor.derivation() | 1.0 | 1.0 | 1.0 |
| CosFactor.CosFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| CosFactor.derivation() | 2.0 | 3.0 | 3.0 |
| CosFactor.toString() | 3.0 | 3.0 | 3.0 |
| Factor.Factor(String,BigInteger) | 1.0 | 1.0 | 1.0 |
| Factor.getDegree() | 1.0 | 1.0 | 1.0 |
| Factor.getType() | 1.0 | 1.0 | 1.0 |
| Judge.canAdd(Term,Term) | 2.0 | 3.0 | 5.0 |
| Judge.canShort(ArrayList,ArrayList,int,int) | 1.0 | 3.0 | 3.0 |
| Judge.canSub1(Term,Term) | 2.0 | 2.0 | 6.0 |
| Judge.canSub2(Term,Term) | 2.0 | 2.0 | 6.0 |
| MainClass.circulation(ArrayList) | 1.0 | 2.0 | 2.0 |
| MainClass.getDerivative(ArrayList) | 1.0 | 4.0 | 4.0 |
| MainClass.main(String[]) | 1.0 | 6.0 | 6.0 |
| MainClass.merge(ArrayList) | 6.0 | 6.0 | 8.0 |
| MainClass.optimize(ArrayList) | 5.0 | 11.0 | 12.0 |
| MainClass.parsePoly(String,Pattern[],ArrayList) | 2.0 | 5.0 | 6.0 |
| MainClass.parseTerm(Pattern[],Matcher,BigInteger,ArrayList) | 5.0 | 10.0 | 10.0 |
| MainClass.poly(String) | 2.0 | 2.0 | 4.0 |
| MainClass.produceCos(String) | 1.0 | 2.0 | 2.0 |
| MainClass.producePower(String) | 3.0 | 2.0 | 3.0 |
| MainClass.produceSin(String) | 1.0 | 2.0 | 2.0 |
| Merge.mergeAdd(int,int,ArrayList) | 1.0 | 4.0 | 4.0 |
| Merge.mergeSub1(int,int,ArrayList) | 1.0 | 2.0 | 2.0 |
| Merge.mergeSub2(int,int,ArrayList) | 1.0 | 2.0 | 2.0 |
| PowerFactor.derivation() | 3.0 | 3.0 | 3.0 |
| PowerFactor.PowerFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| PowerFactor.toString() | 3.0 | 3.0 | 3.0 |
| SinFactor.derivation() | 2.0 | 3.0 | 3.0 |
| SinFactor.SinFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| SinFactor.toString() | 3.0 | 3.0 | 3.0 |
| Term.compareTo(Term) | 6.0 | 5.0 | 6.0 |
| Term.Diffs(Term) | 2.0 | 5.0 | 5.0 |
| Term.equals(Object) | 4.0 | 1.0 | 6.0 |
| Term.getCoefficient() | 1.0 | 1.0 | 1.0 |
| Term.getCosDegree() | 1.0 | 1.0 | 1.0 |
| Term.getFactors() | 1.0 | 1.0 | 1.0 |
| Term.getPowerDegree() | 1.0 | 1.0 | 1.0 |
| Term.getSinDegree() | 1.0 | 1.0 | 1.0 |
| Term.Term() | 1.0 | 1.0 | 1.0 |
| Term.Term(ArrayList) | 1.0 | 9.0 | 9.0 |
| Term.Term(BigInteger) | 1.0 | 1.0 | 1.0 |
| Term.Term(BigInteger,ArrayList) | 1.0 | 7.0 | 7.0 |
| Term.toString() | 7.0 | 7.0 | 9.0 |
| Total | 90.0 | 137.0 | 162.0 |
| Average | 2.0 | 3.0444 | 3.6 |
由于这次解析工作放到了主类里,而且本身使用的正则表达式解析出现了神奇的bug,于是我使用了逐层解析,只用小正则,这提升了正确性,也使逻辑清晰了,但是解析篇幅变长,但由于是在提交之后修改bug阶段重写的,时间有些紧,于是便放在了主类里,使主类代码过于臃肿。加上Term类的计算方法过多,以及不同的构造方法,使Term类也代码量较大。该部分在第三次作业会进行改进。另外优化方法放在外边,传参调用,在这次较为简单的结构中尚可存活,但是在下次作业遇到了bug,稍后进行分析。
bug分析
个人bug
这次作业bug聚集在解析和优化两个部分。
首先是解析部分。由于本人正则表达式掌握的不够熟练,导致在写完程序后提交发现解析出现了bug。在调试之后,发现了是正则表达式非贪婪匹配的问题。本想着改正则表达式,但是想起下次作业,最后决定层层解析,改用小正则。由于解析部分比较重要,反复调试之后我才将它和我的后端链接了起来,确保解析正确是本程序成功的第一步。
其次是优化。参见大佬的讨论区帖子,优化的思路非常清晰,对于擅长数(百)学(度)的我们而言,最重要的就是写的时候要多加小心。在搞清楚合并情况之后,我们知道Sin类对象和Cos对象的相关代码具有很强的相似性,我们在复制粘贴的时候,一定要记得改!过!来!不然就会像我一样在互测中悲催的将Sin类型试图转换成Cos类型而报错,输出WF。这一切都是因为我在写判断函数的时候没有把C变为S。
别人bug
由于自己测试自己的程序的时候发现了一个优化操作x * * 2 ---> x * x的时候直接使用replaceAll会把
x * * 200替换成 x * x00的现象,所以互测时试了一下这个数据,果然刀中了朋友。其次就是有的同学不听指导书的建议,使用静态数组,结果数组越界,导致程序re的惨剧....
第三次作业
程序结构分析
UML类图

程序讲解
本次作业加入了嵌套结构,使得解析成为了难点。在了解过递归下降算法后,我决定在解析的时候利用该方法进行。本次程序吸取前两次的教训,书写了专门的Parser类,在其中层层解析(方法和第二次较为相似)。通过层层解析Poly(多项式,通过getPoly方法),Term(项,通过getTerm方法),Factor(因子,通过getFactor方法),ConsFactor(常数因子,通过getCons方法),CosFactor、SinFactor(三角函数因子,在判断具体使用哪种方法的时候采用了根据自定义的FIRST集来实现,之后分别通过getCosFactor以及getSinFactor方法),PoweFactor(指数因子,通过getPower方法),degree(指数,getDegree方法),其中,PowerFactor、ConsFactor不会进入更深层的递归,三角函数则根据内部因子(InnerFactor)的类型决定是否进入更深层递归,而PolyFactor必然有一个内部的Poly,在这里,本人先将其左括号跳过,之后对Poly进行解析。
求导过程较为关键,在延续上次作业的基础上需要修改Sin和Cos的求导方法,同时表述Poly的求导方法(遍历收集Term导数即可)
之前的几个类均仍存在,此外增加了Poly类,同时修改了SinFactor和CosFactor类(由于内部因子多样化),同时每个类增加了优化方法进行优化操作。
耦合度分析
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| ConsFactor.ConsFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| ConsFactor.derivation() | 1.0 | 1.0 | 1.0 |
| ConsFactor.equals(Object) | 3.0 | 1.0 | 3.0 |
| ConsFactor.optimization() | 1.0 | 1.0 | 1.0 |
| ConsFactor.toString() | 1.0 | 1.0 | 1.0 |
| CosFactor.CosFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| CosFactor.CosFactor(BigInteger,Factor) | 1.0 | 1.0 | 1.0 |
| CosFactor.derivation() | 3.0 | 4.0 | 4.0 |
| CosFactor.equals(Object) | 6.0 | 4.0 | 8.0 |
| CosFactor.getInnerFactor() | 1.0 | 1.0 | 1.0 |
| CosFactor.optimization() | 2.0 | 2.0 | 3.0 |
| CosFactor.toString() | 4.0 | 4.0 | 4.0 |
| Factor.Factor(String,BigInteger) | 1.0 | 1.0 | 1.0 |
| Factor.getDegree() | 1.0 | 1.0 | 1.0 |
| Factor.getType() | 1.0 | 1.0 | 1.0 |
| Factor.upToTerm() | 1.0 | 1.0 | 1.0 |
| Judge.canMergeCons(Factor,Factor) | 3.0 | 3.0 | 4.0 |
| Judge.canMergeCos(Factor,Factor) | 6.0 | 4.0 | 9.0 |
| Judge.canMergeFactor(Factor,Factor) | 8.0 | 6.0 | 9.0 |
| Judge.canMergePolyFactor(Factor,Factor) | 1.0 | 1.0 | 1.0 |
| Judge.canMergePower(Factor,Factor) | 3.0 | 3.0 | 4.0 |
| Judge.canMergeSin(Factor,Factor) | 6.0 | 4.0 | 9.0 |
| Judge.canMergeTerm(Term,Term) | 8.0 | 3.0 | 10.0 |
| MainClass.main(String[]) | 1.0 | 3.0 | 3.0 |
| Merge.mergeCons(Factor,Factor) | 1.0 | 1.0 | 1.0 |
| Merge.mergeCos(Factor,Factor) | 1.0 | 1.0 | 1.0 |
| Merge.mergeFactor(Factor,Factor) | 5.0 | 5.0 | 5.0 |
| Merge.mergePolyFactor(Factor,Factor) | 1.0 | 1.0 | 1.0 |
| Merge.mergePower(Factor,Factor) | 1.0 | 1.0 | 1.0 |
| Merge.mergeSin(Factor,Factor) | 1.0 | 1.0 | 1.0 |
| Merge.mergeTerm(Term,Term) | 1.0 | 1.0 | 1.0 |
| Parser.bracketCheck(String) | 1.0 | 2.0 | 4.0 |
| Parser.clearBlank() | 1.0 | 2.0 | 3.0 |
| Parser.getCosFactor() | 2.0 | 1.0 | 2.0 |
| Parser.getDegree() | 3.0 | 2.0 | 3.0 |
| Parser.getFactor() | 6.0 | 6.0 | 6.0 |
| Parser.getInnerFactor() | 5.0 | 2.0 | 5.0 |
| Parser.getPoly() | 2.0 | 6.0 | 7.0 |
| Parser.getPolyFactor() | 1.0 | 1.0 | 1.0 |
| Parser.getPowerFactor() | 2.0 | 2.0 | 2.0 |
| Parser.getSinFactor() | 2.0 | 1.0 | 2.0 |
| Parser.getTerm() | 1.0 | 5.0 | 6.0 |
| Parser.Parser(String) | 3.0 | 1.0 | 3.0 |
| Poly.delete() | 1.0 | 4.0 | 4.0 |
| Poly.Diffs() | 1.0 | 3.0 | 3.0 |
| Poly.equals(Object) | 6.0 | 5.0 | 10.0 |
| Poly.getTerms() | 1.0 | 1.0 | 1.0 |
| Poly.mergeSameTerm() | 1.0 | 4.0 | 4.0 |
| Poly.Poly() | 1.0 | 1.0 | 1.0 |
| Poly.Poly(ArrayList) | 1.0 | 1.0 | 1.0 |
| Poly.toString() | 3.0 | 3.0 | 4.0 |
| Poly.toTerm() | 3.0 | 2.0 | 3.0 |
| PolyFactor.cloneInnerPoly() | 1.0 | 1.0 | 1.0 |
| PolyFactor.derivation() | 1.0 | 1.0 | 1.0 |
| PolyFactor.equals(Object) | 4.0 | 4.0 | 6.0 |
| PolyFactor.getPolyIn() | 1.0 | 1.0 | 1.0 |
| PolyFactor.optimization() | 3.0 | 3.0 | 3.0 |
| PolyFactor.PolyFactor(Poly) | 1.0 | 1.0 | 1.0 |
| PolyFactor.toString() | 1.0 | 1.0 | 1.0 |
| PowerFactor.derivation() | 3.0 | 3.0 | 3.0 |
| PowerFactor.equals(Object) | 3.0 | 1.0 | 3.0 |
| PowerFactor.optimization() | 1.0 | 1.0 | 1.0 |
| PowerFactor.PowerFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| PowerFactor.toString() | 3.0 | 3.0 | 3.0 |
| SinFactor.derivation() | 3.0 | 4.0 | 4.0 |
| SinFactor.equals(Object) | 6.0 | 4.0 | 8.0 |
| SinFactor.getInnerFactor() | 1.0 | 1.0 | 1.0 |
| SinFactor.optimization() | 2.0 | 2.0 | 3.0 |
| SinFactor.SinFactor(BigInteger) | 1.0 | 1.0 | 1.0 |
| SinFactor.SinFactor(BigInteger,Factor) | 1.0 | 1.0 | 1.0 |
| SinFactor.toString() | 4.0 | 4.0 | 4.0 |
| Term.canDownToFactor() | 4.0 | 2.0 | 4.0 |
| Term.cloneFactors() | 1.0 | 1.0 | 1.0 |
| Term.containOnlyPolyFactor() | 4.0 | 1.0 | 4.0 |
| Term.deleteUseless() | 4.0 | 4.0 | 5.0 |
| Term.Diffs() | 2.0 | 5.0 | 5.0 |
| Term.downToFactor() | 4.0 | 3.0 | 4.0 |
| Term.equals(Object) | 10.0 | 3.0 | 11.0 |
| Term.getCoefficient() | 1.0 | 1.0 | 1.0 |
| Term.getFactors() | 1.0 | 1.0 | 1.0 |
| Term.mergeConstant() | 1.0 | 3.0 | 3.0 |
| Term.mergeSameFactor() | 1.0 | 4.0 | 4.0 |
| Term.optimization() | 5.0 | 7.0 | 7.0 |
| Term.Term() | 1.0 | 1.0 | 1.0 |
| Term.Term(ArrayList) | 1.0 | 3.0 | 3.0 |
| Term.Term(BigInteger) | 1.0 | 1.0 | 1.0 |
| Term.Term(BigInteger,ArrayList) | 1.0 | 3.0 | 3.0 |
| Term.Term(Factor) | 1.0 | 1.0 | 1.0 |
| Term.toString() | 7.0 | 7.0 | 9.0 |
| Total | 214.0 | 208.0 | 283.0 |
| Average | 2.40449 | 2.337079 | 3.18 |
本程序可以划分为多个层次Poly,Term,Factor。其中Factor又包括ConsFactor,CosFactor,SinFactor,PoweFactor。他们的上下级别分明,也使得解析和求导思路也很明确,就是在层层递归,属于谁的工作就交给谁来完成,从而逐步达到目的。
对于功能的实现,和第二次类似,采用了两个单独的类Merge类以及Judge类,来进行优化判断和合并实现。由于这两类涵盖了几乎所有的判断和合并操作,导致方法种类较多,故篇幅较大比较臃肿。可以考虑将没种类对应的方法放入类内部。而对于功能较多的Term类和Poly类,现在思考其实可以将其求导和优化分开从而降低程序耦合度。
吸取上次的教训,将解析部分提出,大大降低了主类的代码量,也使程序更加结构化,一定程度上降低了耦合度。但是对工厂模式的使用不够到位,使类创建过程仍较为重复,在参考了优秀代码后有了新的启发。
bug分析
个人bug
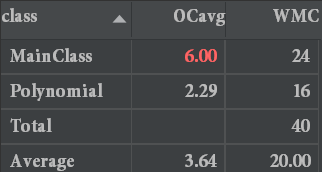
这次作业bug仍然聚集在解析和优化两个部分,同时由于嵌套结构,CPU超时也变得很容易出现 。
由于吃了之前的亏,加上对这次的作业稍有准备,解析部分顺利完成,并在完成之后反复检验了其正确性之后才进行之后的编程。同时为程序设定解析部分"输出按钮",确保每一次的解析结果是否输出可以由我们自由掌控,这样为后期找bug提供了很大的帮助。
本身这次作业的难度就很高,加上优化会使bug翻倍增长。可以说优化和debug的时间三七分成。本人本身计划像上次作业一样在外部优化,甚至写好了专门的优化类。在完成第一版优化后,开始测试。发现一切都和我想的不一样。出现了结果丢失系数,指数的神必现象。经过单步调试,我发现了原因所在。由于外部优化,我们是在不断地传递对象和返回对象,那么本身优化的对象没有发生改变,而是返回了新的对象。那么在进行嵌套优化的时候就会由于优化顺序的不确定性导致新旧对象的交替出现情况,最后严重影响程序的正确性。
本身,本人准备在每个类增加刷新操作,但是考虑到对象的思想,我决定最终将这个优化方法变成上述层次对象的属性,这样对每一个对象优化后自动更新该对象,不会出现之前所述的bug。
对于CPU超时,我在写本次作业之前的印象就是算法问题,没救了,但是在经历了这次的作业,我发现拖慢程序的不一定是算法,还可能是我的编程不良习惯。
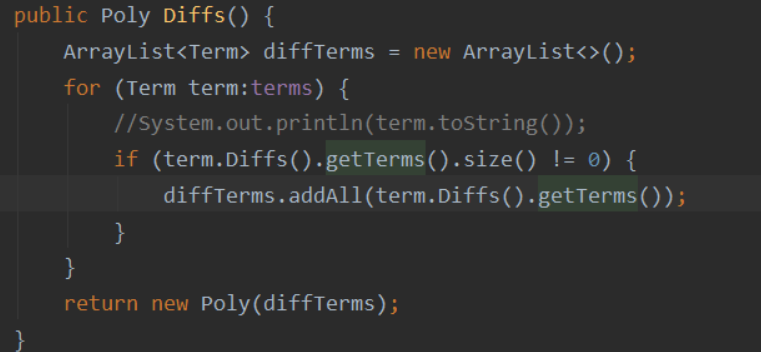
上图!
上图是我本身的代码,可以看到,在for循环之中本人对于term进行了两次求导操作,分别是if括号中以及if执行语句中。那么这样一来可不简单是*2的区别,首先是2的指数次的调用,其次由于嵌套结构,还会反复调用其他求导方法,这样下来就会大大增加程序的运行时间。修改后代码如下:
就这样一个简单的操作,就拯救了CPU超时问题了。
总算,努力没有白费,这次作业安详地通过了强测和互测的检验,原来不用修复bug的周二中午是这么的美好...
别人bug
首先,由于自身找bug的经验,我在互测时首先卡超时,果然卡到了一位朋友。之后在进行随机样例测试检验了求导的正确性后,开始对优化进行检验。将事先准备的合并优化测试数据、去括号优化测试数据、还有我没做的x**2的替换优化数据逐一检验。朋友们都通过了检验。再试一下随机数据,跑不出来,结束hack。
三次作业迭代分析
第一次作业写成了大杂烩,不具有拓展性,在这里跳过比对......
第二次作业为第三次作业创建了很好的架构,层次化的类已经建立好,只需要增加类别种类,修改部分方法即可。求导部分剩下来的时间可以更多的用于思考优化和进行正确性检验。
第三次作业同第二次作业相比,主要做出了以下改变:
1.将解析部分单独成类。由于这次的解析较为复杂,如果还在主类进行,可读性太差,可能自己都不想多看一眼自己的代码,并且容易出错。
2.增加多项式类以及多项式因子类。第二次作业对于Term的求导尚可用一个ArrayList表示,但这次,由于求导也是递归进行,如果不返回一个具体的对象,那么递归将很难进行下去。那么对于Term,他的求导结果是一个多项式,自然而然我们需要Poly类。况且,多项式因子的存在感极强,而其本质虽然是一个加了括号的Term集合,但如果不单独创建对象,则还会对解析造成极大的困扰。
3.将优化方法放在每一个对象中,局部优化出错概率比整体优化要小,调试的时候也更加便利,何乐不为。
心得体会
关于面向对象编程思想
经历了这三次作业,我对面向对象的编程思想有了更深的体会。面向对象的一大好处就是使我们的程序结构化,便于我们实现高内聚低耦合。通过封装、继承和多态的应用,我逐渐培养了面向对象的程序设计思维。
封装:找到变化并且把它封装起来,我们就可以在不影响其它部分的情况下修改或扩展被封装的变化部分,这是迭代开发非常重要的手段,也是编写可扩展程序的基础。
继承:子类继承父类,可以继承父类的方法及属性,实现了多态以及代码的重用,因此也解决了系统的重用性和扩展性。并且我发现继承是在在程序开发过程中重构得到的,而不是程序设计之初就使用继承。就像我在第一次作业根本不会想到继承,在书写第二次作业时发现不同因子的相似特征从而采用了继承。我觉得继承是一个顺其自然的过程,它可以做到完善程序的功能,拓展实现功能,使我们的逻辑更加清晰。
多态:通过接口的使用,我更加熟悉了多态。接口是对行为的抽象,刚才在封装提到,找到变化部分并封装起来,但是封装起来后,怎么适应接下来的变化?这正是接口的作用,接口的主要目的是为不相关的类提供通用的处理服务,我们可以想象一下。比如鸟会飞,但是飞机也会飞,通过飞这个接口,我们可以让鸟和飞机,都实现这个接口,这就实现了系统的可维护性,可扩展性,同时也方便了我们不同类别相似方法的调用。
通过实践,我渐渐适应了OO的思想;借助练习,我了解了OO的节奏。每周的代码作业都是一个新的挑战,也都是一次属于自己的设计,相信通过之后的训练,我能够学习到更多的设计思路,提升自己的工程化能力。
关于创建模式
随着作业难度的提升,创建对象已经不是最初简单的new+构造方法,尤其是第三次作业中不同项之间的计算得到的新的对象。因此,适当地使用工厂模式,可以使代码更加简明,避免了每次实例化对象时的代码重复。工厂模式的好处,通过近段时间的练习,我们都有了深刻的体会,相信在之后的任务中也会有更加广泛的应用。
关于设计的重要性
OO和之前所学的C语言以及数据结构的显著区别首先就是代码量的陡增。之前在C语言一main到底,在python中不单独封装类尚可苟活,如今在OO如果还是以过数据点为程序的终极目标,那往往设计出数据点也过不了还不好修bug的程序。
其实经历了第一次作业,我对于设计重要性的体会不是很深刻。但是在第二次老师们的善意提醒后,我才有了设计的概念,逐步去思考代码复用性及可扩展性,第三次作业还能不能存活。这对于工程化程序设计是非常重要的,也是编程的难点。但是在做出了精心的设计后,我发现写代码时,每一个模块的目标非常清晰,就会使思路更为流畅,一气呵成。并且,之后的测试也因为明确了设计的难点,而更容易找到出错之处。因此不管时间多么紧迫,设计的时间是省不得的。
第一单元已经结束,希望第二单元可以设计出更好的代码。