序列分割
Time Limit: 40 Sec Memory Limit: 128 MB[Submit][Status][Discuss]
Description
Input
输入第一行包含两个整数n,k(k+1≤n)。
第二行包含n个非负整数a1,a2,...,an(0≤ai≤10^4),表示一开始小H得到的序列。
Output
输出第一行包含一个整数,为小H可以得到的最大分数。
Sample Input
4 1 3 4 0 2 3
Sample Output
在样例中,小H可以通过如下3轮操作得到108分:
1.开始小H有一个序列(4,1,3,4,0,2,3)。
小H选择在第1个数之后的位置将序列分成两部分,并得到4×(1+3+4+0+2+3)=52分。
2.这一轮开始时小H有两个序列:(4),(1,3,4,0,2,3)。
小H选择在第3个数字之后的位置将第二个序列分成两部分,并得到(1+3)×(4+0+2+3)=36分。
3.这一轮开始时小H有三个序列:(4),(1,3),(4,0,2,3)。
小H选择在第5个数字之后的位置将第三个序列分成两部分,并得到(4+0)×(2+3)=20分。
经过上述三轮操作,小H将会得到四个子序列:(4),(1,3),(4,0),(2,3)并总共得到52+36+20=108分。
HINT
2≤n≤100000 , 1≤k≤min(n -1,200)。
Main idea
将一个序列分成k段,定义权值和为两两段的累加和的乘积,求出最大权值和。
Source
首先发现n<=10^5,k<=200,我们先想这应该是一道DP,然后发现了原题中的操作(每次分为两段然后再分)经过分配是可以转化为题意这样的,这样的话答案就与分的顺序无关了。
一开始我想到了一个O(n^3*k)的做法,每次分割出i~j段,然后发现由于与顺序无关这个性质,可以转化成每次分割第i个位置, 那么我们得到了状态:f[a][i]表示分割第a次,第a次在第i个位置分的答案。
然后立马想到了转移方程:f[a][i]=max(f[a][i],f[a-1][j]+s[j]*(s[i]-s[j])) (其中s[i]表示1~i的和),这样的话效率是O(n^2*k),然后我们考虑如何优化。大胆猜测可以使用斜率优化。
首先假定k<j,且j的决策更优,那么使得条件成立的式子(以下f[j]表示f[a-1][j]):
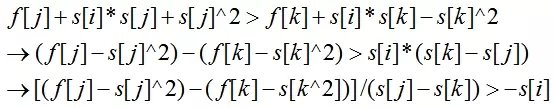
令x[i]表示f[a-1][i]-s[i]*s[i],y[i]表示s[i],该式子即可表示为:(x[j]-x[k]) / (y[j]-y[k]) > -s[i]。
然后斜率优化维护一下上凸壳(取max值)即可,效率即为O(n*k)。
注意一下内存限制128MB,所以我们将第一维a滚动即可,由于用的是斜率优化维护凸壳,所以我们一开始需要将a[i]=0的去掉否则答案会偏小。
PS:
总结一下斜率优化推式子的精髓:假定k<j且j的决策更优,然后列出不等式,去掉只与i有关的项(这时候可能存在s[j]*s[i]这种项式),然后将不等式移项,使得不等号右边仅有与s[i]有关的项(即与j,k无关),然后根据最大值或者最小值决定维护上凸壳或下凸壳。
Code

1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cstring> 5 #include<cstdlib> 6 #include<cmath> 7 using namespace std; 8 9 const int ONE=100001; 10 11 int T,n,m; 12 int a[ONE]; 13 int tou,wei; 14 long long s[ONE]; 15 long long f[3][ONE]; 16 int q[ONE]; 17 18 int get() 19 { 20 int res=1,Q=1;char c; 21 while( (c=getchar())<48 || c>57 ) 22 if(c=='-')Q=-1; 23 res=c-48; 24 while( (c=getchar())>=48 && c<=57 ) 25 res=res*10+c-48; 26 return res*Q; 27 } 28 29 double slope(int a,int j,int k) 30 { 31 double xj,xk,yj,yk; 32 xj=f[!a][j]-s[j]*s[j]; xk=f[!a][k]-s[k]*s[k]; 33 yj=s[j]; yk=s[k]; 34 return (xj-xk)/(yj-yk); 35 } 36 37 int main() 38 { 39 // freopen("s.in","r",stdin); 40 //freopen("s.out","w",stdout); 41 T=get(); m=get(); 42 43 int begin=0; 44 for(int i=1;i<=T;i++) 45 { 46 a[i]=get(); 47 if(a[i]) a[++n]=a[i]; 48 } 49 for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i]; 50 51 int A=0,B=1,jishu=0; 52 for(int a=1;a<=m;a++) 53 { 54 swap(A,B); 55 tou=wei=1; 56 for(int i=1;i<=n;i++) 57 { 58 while(tou<wei && slope(B,q[wei],q[wei-1]) < slope(B,i,q[wei])) wei--; 59 q[++wei]=i; 60 61 while(tou<wei && slope(B,q[tou+1],q[tou]) > -s[i]) tou++; 62 63 f[B][i]=max(f[B][i],f[A][q[tou]] + s[i]*s[q[tou]] - s[q[tou]]*s[q[tou]] ); 64 } 65 } 66 67 printf("%lld",f[B][n]); 68 }
