设计思路
首先利用随机数生成一个二维数组,可以控制生成随机数的范围,利用宏定义表示长和宽控制二维数组的大小。求最大子数组的和需要利用上一篇博客(求一维数组最大子数组的和)的方法,采取逐行轮换相加的方法依次求若干行的最大子数组的和,利用一个一维数组来储存逐行轮换相加得到的一维数组,再在该数组里求一维数组的最大子数组的和,这样就把二维数组转换成了一维数组,问题就迎刃而解了。
源程序代码
#include<iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
#define M 4
#define N 4
void main()
{
int m=4,n=4,a[100][100],i,j,b,c,z;
cout<<"请输入数值范围:"<<endl;
cin>>b>>c;
cout<<"生成二维数组为:"<<endl;
srand(unsigned(time(0)));
for(i=0;i<M;i++)
{
for(j=0;j<N;j++)
{
a[i][j]=rand()%(c-b+1)+b;
cout<<a[i][j]<<" ";
}
cout<<endl;
}
int sum,s[100],k=0,o=-1000,p=-1000,q=-1000;
for(j=0;j<N;j++)
{
s[j]=0;
}
for(int ii=0;ii<M;ii++)
{
while(k+ii<M)
{
for(j=0;j<N;j++)
{
s[j]=s[j]+a[k+ii][j];
}
for (i=0;i<N;i++)
{
for (j=i;j<N;j++)
{
sum=0;
for (z=i;z<=j;z++)
{
sum=sum+s[z];
}
if (sum>o) o=sum;
}
if (o>p)
{
p=o;
}
}
k++;
}
if (p>q)
{
q=p;
}
k=0;
for(j=0;j<N;j++)
{
s[j]=0;
}
}
cout<<"子矩阵最大值为"<<q<<endl;
}
运行结果截图
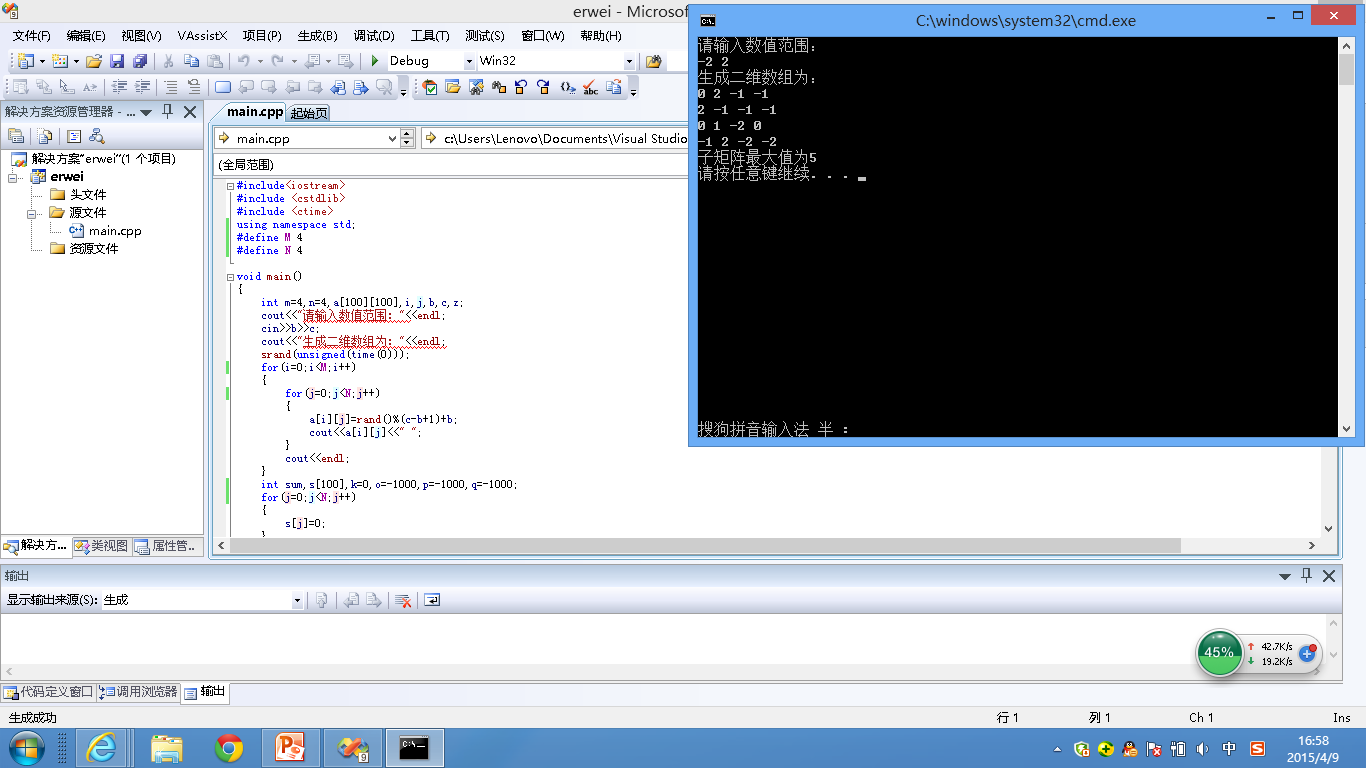
编程总结
想办法把二维数组转换为一维数组,这样就使问题变得简单容易思考,化繁为简的思想贯穿始终。编写新程序的时候要善于利用之前写好的程序,所以就需要保存之前写的程序,不能随意丢弃。