Python真题练习：1001-害死人不偿命的(3n+1)猜想、1002-写出这个数、1006-换个格式输出整数、1011-A+B和C

1001——害死人不偿命的(3n+1)猜想 

卡拉兹(Callatz)猜想：

对任何一个正整数 $n$，如果它是偶数，那么把它砍掉一半；如果它是奇数，那么把(3n+1)砍掉一半。这样一直反复砍下去，最后一定在某一步得到 $n=1$。卡拉兹在1950年的世界数学家大会上公布了这个猜想，传说当时耶鲁大学师生齐动员，拼命想证明这个貌似很傻很天真的命题，结果闹得学生们无心学业，一心只证(3n+1)，以至于有人说这是一个阴谋，卡拉兹是在蓄意延缓美国数学界教学与科研的进展……

我们今天的题目不是证明卡拉兹猜想，而是对给定的任一不超过 1000 的正整数 $n$，简单地数一下，需要多少步（砍几下）才能得到 $n=1$？

输入格式：

每个测试输入包含 1 个测试用例，即给出正整数 $n$ 的值。

输出格式：

输出从 $n$ 计算到 1 需要的步数。

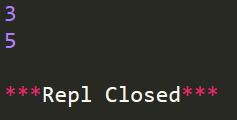
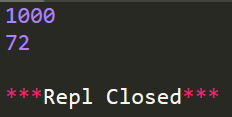
输入样例：

3

输出样例：

5

代码实现：

def Callatz(n):
    N=0
    while n!=1:
        if n%2==0:
            n=n/2
        else:
            n=(3*n+1)/2
        N+=1
        if n==1:
            break
    return N

n=eval(input())
print(Callatz(n))

运行结果：

 

1002——写出这个数

读入一个正整数 $n$，计算其各位数字之和，用汉语拼音写出和的每一位数字。

输入格式：

每个测试输入包含 1 个测试用例，即给出自然数 $n$ 的值。这里保证 $n$ 小于10^100。

输出格式：

在一行内输出 $n$ 的各位数字之和的每一位，拼音数字间有 1 空格，但一行中最后一个拼音数字后没有空格。

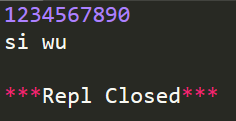
输入样例：

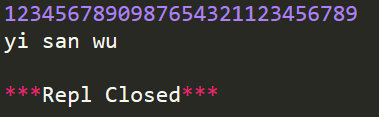
1234567890987654321123456789

输出样例：

yi san wu

代码实现：

def WriteNum(n):
    s=0
    l=[]
    if 0<=len(n)<=101:
        for i in range(len(n)):
            s+=int(n[i])
        for j in str(s):
            if j=='1':
                r='yi'
            elif j=='2':
                r='er'
            elif j=='3':
                r='san'
            elif j=='4':
                r='si'
            elif j=='5':
                r='wu'
            elif j=='6':
                r='liu'
            elif j=='7':
                r='qi'
            elif j=='8':
                r='ba'
            elif j=='9':
                r='jiu'
            elif j=='0':
                r='ling'
            l.append(r)
    print(' '.join(l))

n=input()
WriteNum(n)

运行结果：

 

 1006——换个格式输出整数

让我们用字母B来表示“百”、字母S表示“十”，用12...n来表示不为零的个位数字n (<10)，换个格式来输出任一个不超过3位的正整数。例如234应该被输出为BBSSS1234， 因为它有2个“百”、3个“十”、以及个位的4。

输入格式：

每个测试输入包含1个测试用例，给出正整数n(<1000)。

输出格式：

每个测试用例的输出占一行，用规定的格式输出 n。

输入样例 1：

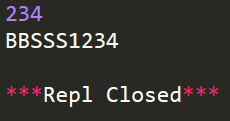
234

输出样例 1：

BBSSS1234

输入样例 2：

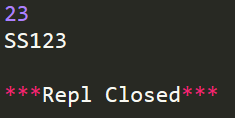
23

输出样例 2：

SS123

代码实现：

def TransInt(n):
    a=[]
    b=[]
    c=[]
    B=int((n-n%100)/100)
    S=int((n%100-(n%100)%10)/10)
    G=(n%100)%10
    if 0<n<1000:
        if 0<B<10:
            for i in range(B):
                i='B'
                a.append(i)
        Bp=''.join(a)
        if 0<S<10:
            for j in range(S):
                j='S'
                b.append(j)
        Sp=''.join(b)
        if 0<G<10:
            for k in range(G):
                c.append(k+1)        
        Gp=''.join('%s' %g for g in c)
    return Bp+Sp+Gp

n=eval(input())
print(TransInt(n))

运行结果：

 

 

 1011——A+B 和 C

给定区间[-2^31,2^31]内的3个整数A、B和C,请判断A+B是否大于C。

输入格式：

输入第1行给出正整数T (<=10)，是测试用例的个数。随后给出T组测试用例，每组占一行，顺序给出A、B和C。整数间以空格分隔。

输出格式：

对每组测试用例，如果A+B>C, 在一行中输出Case #X: true, 否则输出Case #X: false, 其中X是测试用例的编号(从1开始)。

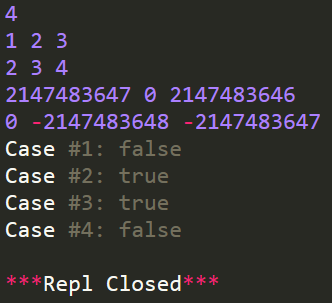
输入样例：

4
1 2 3
2 3 4
2147483647 0 2147483646
0 -2147483648 -2147483647

输出样例：

Case #1: false
Case #2: true
Case #3: true
Case #4: false

代码实现：

def ABC(n):
    for i in range(n):
        a=input().split()
        if int(a[0])+int(a[1])>int(a[2]):
            print('Case #'+str(i+1)+': true')
        else:
            print('Case #'+str(i+1)+': false')

n=int(input())
ABC(n)

运行结果：