洛谷题目链接:[ZJOI2012]旅游
题目描述
到了难得的暑假,为了庆祝小白在数学考试中取得的优异成绩,小蓝决定带小白出去旅游~~
经过一番抉择,两人决定将T国作为他们的目的地。T国的国土可以用一个凸N边形来表示,N个顶点表示N个入境/出境口。T国包含N-2个城市,每个城市都是顶点均为N边形顶点的三角形(换而言之,[b]城市组成了关于T国的一个三角剖分[/b])。[b]两人的旅游路线可以看做是连接N个顶点中不相邻两点的线段[/b]。
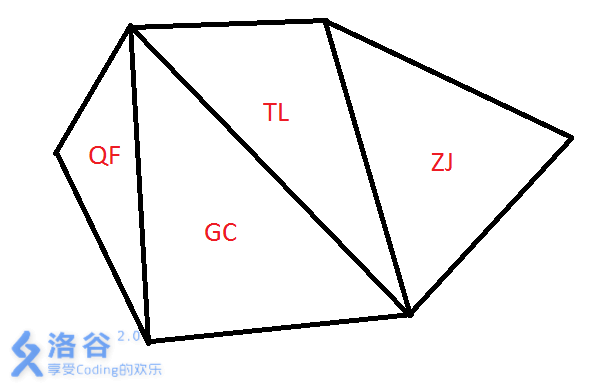
为了能够买到最好的纪念品,小白希望旅游路线上经过的城市尽量多。作为小蓝的好友,你能帮帮小蓝吗?
输入输出格式
输入格式:
每个输入文件中仅包含一个测试数据。
第一行包含两个由空格隔开的正整数N,N的含义如题目所述。
接下来有N-2行,每行包含三个整数 p,q,r,表示该城市三角形的三个顶点的编号(T国的N个顶点按顺时间方向从1至n编号)。
输出格式:
输出文件共包含1行,表示最多经过的城市数目。([b]一个城市被当做经过当且仅当其与线路有至少两个公共点[/b])
输入输出样例
输入样例#1:
6
1 2 4
2 3 4
1 4 5
1 5 6
输出样例#1:
4
说明
对于20%的数据, n<=2000
对于100%的数据, 4<=n<=200000
一句话题意: 给出一个 奇奇怪怪的(??) 多边形,其中每(3)条边围成一个城市,每两个相连的城市中有一条边,问从任意一个城市出发不重复经过某个城市最多能经过多少个城市.
题解: 首先对于这种奇奇怪怪的题目,我们需要将它转化模型.很显然这个连通关系可以将它转化成一个图论问题.对于这个建边,有一点小技巧,比如我们发现一条边只会连通两个城市,并且一条边一定是由多边形上的两个顶点确定的.所以我们可以将一条边的两个顶点的存入一个结构体内,并用(map)记录第一次与这条边接触的城市是哪一个.这样如果遍历到一个有值的边,就可以直接建边了.
然后我们需要思考这个建出来的图都有些什么性质.一个城市是一个三角形,那么显然它最多与三个城市连边,并且在边界上的城市是不会有三个城市与它相连的.并且在图中不会存在环,也就是两个三角形不可能有超过一条边的公共边.
那么知道这些性质了,我们就会发现它是一棵树,并且如果以边界为根的话,它还是一颗二叉树.
在树上找一条最长的路径,显然就是求树的直径,直接跑一遍(dfs)求出直径就可以了.
#include<bits/stdc++.h>
using namespace std;
const int N = 200000+5;
int n, ecnt = 0, last[N], ans = 0, f[N];
struct edge{
int to, nex, w;
}e[N*2];
struct line{
int x, y;
bool operator < (const line &a) const{
return x == a.x ? y < a.y : x < a.x;
}
};
map <line, int> vis;
void add(int x, int y, int z){
e[++ecnt].to = y, e[ecnt].w = z, e[ecnt].nex = last[x], last[x] = ecnt;
}
void dfs(int x, int fa){
for(int to, i=last[x];i;i=e[i].nex){
to = e[i].to; if(to == fa) continue;
dfs(to, x);
if(ans < f[x]+f[to]+e[i].w) ans = f[x]+f[to]+e[i].w;
if(f[x] < f[to]+e[i].w) f[x] = f[to]+e[i].w;
}
}
int main(){
ios::sync_with_stdio(false);
int x, y, z; cin >> n;
for(int i=1;i<=n-2;i++){
cin >> x >> y >> z;
if(x > y) swap(x, y); if(y > z) swap(y, z); if(x > y) swap(x, y);
if(vis[(line){ x, y }]) add(i, vis[(line){ x, y }], 1), add(vis[(line){ x, y }], i, 1);
else vis[(line){ x, y }] = i;
if(vis[(line){ y, z }]) add(i, vis[(line){ y, z }], 1), add(vis[(line){ y, z }], i, 1);
else vis[(line){ y, z }] = i;
if(vis[(line){ x, z }]) add(i, vis[(line){ x, z }], 1), add(vis[(line){ x, z }], i, 1);
else vis[(line){ x, z }] = i;
}
dfs(1, -1);
cout << ans+1 << endl;
return 0;
}