题目描述
«问题描述:
给定有向图G=(V,E)。设P 是G 的一个简单路(顶点不相交)的集合。如果V 中每个顶点恰好在P 的一条路上,则称P是G 的一个路径覆盖。P 中路径可以从V 的任何一个顶点开始,长度也是任意的,特别地,可以为0。G 的最小路径覆盖是G 的所含路径条数最少的路径覆盖。设计一个有效算法求一个有向无环图G 的最小路径覆盖。
提示:设V={1,2,.... ,n},构造网络G1=(V1,E1)如下:

每条边的容量均为1。求网络G1的( 0 x , 0 y )最大流。
«编程任务:
对于给定的给定有向无环图G,编程找出G的一个最小路径覆盖。
输入输出格式
输入格式:
件第1 行有2个正整数n和m。n是给定有向无环图G 的顶点数,m是G 的边数。接下来的m行,每行有2 个正整数i和j,表示一条有向边(i,j)。
输出格式:
从第1 行开始,每行输出一条路径。文件的最后一行是最少路径数。
输入输出样例
1 4 7 10 11 2 5 8 3 6 9 3
说明
1<=n<=150,1<=m<=6000
可能很多人看到这个提示反而更懵逼了。先解释一下题意,大概就是给你有向图,样例是一张这样的图:
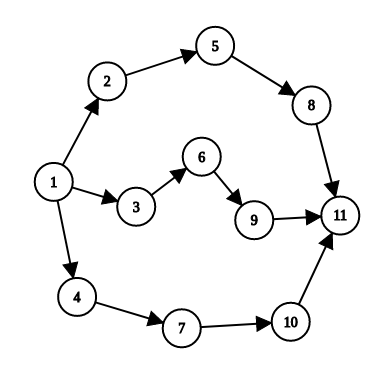
然后求出的最小路径数就是3了,三条路径也很容易可以看出。
我们先考虑一下如何求出二分图的最小路径覆盖。
这里介绍一个定理:
最小路径覆盖数=|G|-二分图最大匹配数(|G|是有向图中的总边数)
为什么是这样的呢?首先我们知道,在二分图中一个点就代表者一条路径。那么如果此时二分图内没有连边,这个公式是成立的。每当二分图内增加一条边,最大匹配数就会+1,而一条匹配边会连接二分图中的两个点,那么两个点间本来有两条路径覆盖,就变成了一条。同理,每加入一条边匹配数就会+1,路径覆盖数就会-1。所以这个公式是成立的。但是这个公式是对二分图适用的,如何将它转化到这个问题上来呢?
这时我们先将一个点拆A成出点Ax和入点Ay,那么在连有向边A -> B的时候就将Ax连向By。就将有向图变成了一个二分图。我们看一下样例转化为二分图的样子(n == 11)。
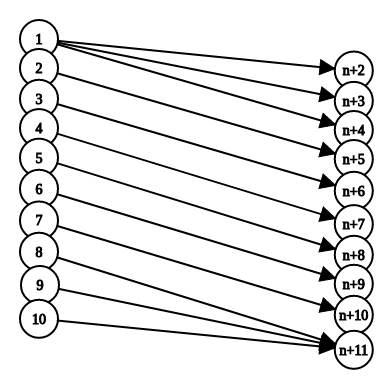
那么这样我们只需要求出将每个点拆点组成二分图后的最大匹配就可以了。
最后在输出路径的时候就记录下每个入点的连入边,然后用并查集记录一下一条路径的起点就好了。
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=15000+5; 4 const int inf=2147483647; 5 6 int n, m, s, t; 7 int cnt = 1; 8 int ans = 0; 9 int last[N*10]; 10 int lev[N*10]; 11 int fa[N*10]; 12 13 struct edge{ 14 int to, next, cap, from; 15 }e[N*10]; 16 17 void add(int x,int y,int z){ 18 e[++cnt].to = y; 19 e[cnt].from = x; 20 e[cnt].cap = z; 21 e[cnt].next = last[x]; 22 last[x] = cnt; 23 } 24 25 bool bfs(){ 26 memset(lev,-1,sizeof(lev)); 27 queue <int> q; lev[s] = 0; q.push(s); 28 while(!q.empty()){ 29 int x = q.front(); q.pop(); 30 for(int i=last[x];i;i=e[i].next){ 31 int to = e[i].to; 32 if(e[i].cap && lev[to] == -1) 33 lev[to] = lev[x]+1 , q.push(to); 34 } 35 } 36 return lev[t] != -1; 37 } 38 39 int dfs(int x,int flow){ 40 if(x == t) return flow; 41 int rest = 0; 42 for(int i=last[x];i;i=e[i].next){ 43 int to = e[i].to; 44 if(lev[to] == lev[x]+1 && e[i].cap){ 45 int f = dfs(to , min(flow-rest,e[i].cap)); 46 if(f){ 47 rest += f; 48 e[i].cap -= f; 49 e[i^1].cap += f; 50 } 51 } 52 } 53 return rest; 54 } 55 56 int find(int x){ 57 if(fa[x] == x) return x; 58 return fa[x] = find(fa[x]); 59 } 60 61 void output(int x){ 62 cout << x << ' '; 63 for(int i=last[x];i;i=e[i].next) 64 if(e[i].cap == 0 && e[i].to > n) 65 output(e[i].to-n); 66 } 67 68 int main(){ 69 int x, y; cin >> n >> m; 70 s = 0 , t = n*2+1; 71 for(int i=1;i<=m;i++){ 72 cin >> x >> y; 73 add(x,y+n,1); add(y+n,x,0); 74 } 75 for(int i=1;i<=n;i++) add(s,i,1),add(i,s,0); 76 for(int i=n+1;i<=n*2;i++) add(i,t,1),add(t,i,0); 77 while(bfs()) ans += dfs(s,inf); 78 for(int i=1;i<=n;i++) fa[i] = i; 79 for(int i=2;i<=cnt;i++){ 80 if(e[i].cap == 0 && e[i].to>n && e[i].to<=n*2 && e[i].from>0 && e[i].from<=n) 81 if(fa[e[i].from] != fa[e[i].to-n]) 82 fa[e[i].to-n] = fa[e[i].from]; 83 } 84 for(int i=1;i<=n;i++) 85 if(fa[i] == i) output(i), cout << endl; 86 cout << n-ans << endl; 87 return 0; 88 }