数据结构与算法--单链表

数据结构

逻辑结构：集合结构，线性结构，树形结构，圆形结构

物理结构：顺序存储结构、链式存储结构

顺序表：数据元素本身连续存储，每个元素所占的存储单元大小固定相同。

元素存储的物理地址（实际内存地址）可以通过存储区的起始地址Loc (e0)加上逻辑地址（第i个元素）与存储单元大小（c）的乘积计算而得，即：　　

　　　　Loc(ei) = Loc(e0) + c*i   

故，访问指定元素时无需从头遍历，通过计算便可获得对应地址，其时间复杂度为O(1)。

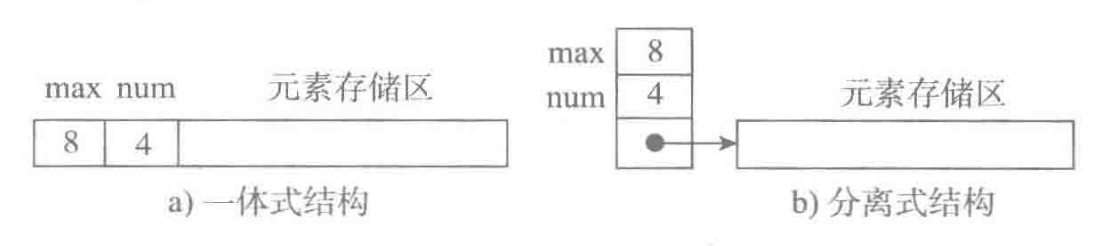
容量与元素个数。 

顺序表结构：一体，分离

链表：

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续存储数据，而是在每一个节点（数据存储单元）里存放下一个节点的位置信息（即地址）。

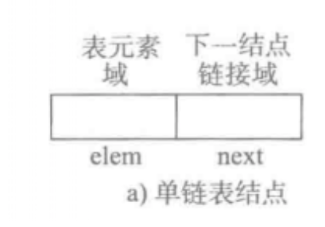
单链表：

表元素域 | 下一个节点链接域 ；首节点称为头变量或者表头指针。

 

如何实现对单链表的操作？

• is_empty() 链表是否为空
• length() 链表长度
• travel() 遍历整个链表
• add(item) 链表头部添加元素
• append(item) 链表尾部添加元素
• insert(pos, item) 指定位置添加元素
• remove(item) 删除节点
• search(item) 查找节点是否存在

3-05：单链表的判空、长度、遍历、尾部添加

class singleLinklist(object)
    "单链表"
    #链表中必须存在某个属性（对象属性），指向头结点。
    def __init__(self，node=None):
        self._head = node  
    
    #下面都是具体的对象方法，不是类方法
    #is_empty() 链表是否为空
    
    def is_empty():
        self._head == None
    pass
    
    #length() 链表长度
    def length(self):
        """链表长度"""
        # cur初始时指向头节点
        cur = self._head
        count = 0
        # 尾节点指向None，当未到达尾部时
        while cur != None:
            count += 1
            # 将cur后移一个节点
            cur = cur.next
        return count
        
    #travel() 遍历整个链表
    def travel(self):
         """遍历链表"""
        cur = self._head
        while cur != None:
             print (cur.item , end=" ")
            cur = cur.next
        print ""
        pass
        

3-06：单链表尾部添加和在指定位置添加

头部添加：

    def add(self, item):
        """头部添加元素"""
        #1.先创建一个保存item值的节点 ，把item封装成一个链表所需要的数据
        node = SingleNode(item)

        #2.将新节点的链接域next指向头节点，即_head指向的位置
        node.next = self._head

        #3.将链表的头_head指向新节点
        self._head = node

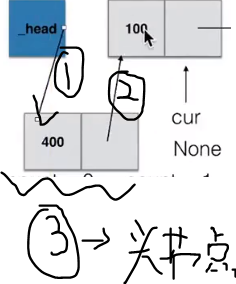
 指定位置添加元素：

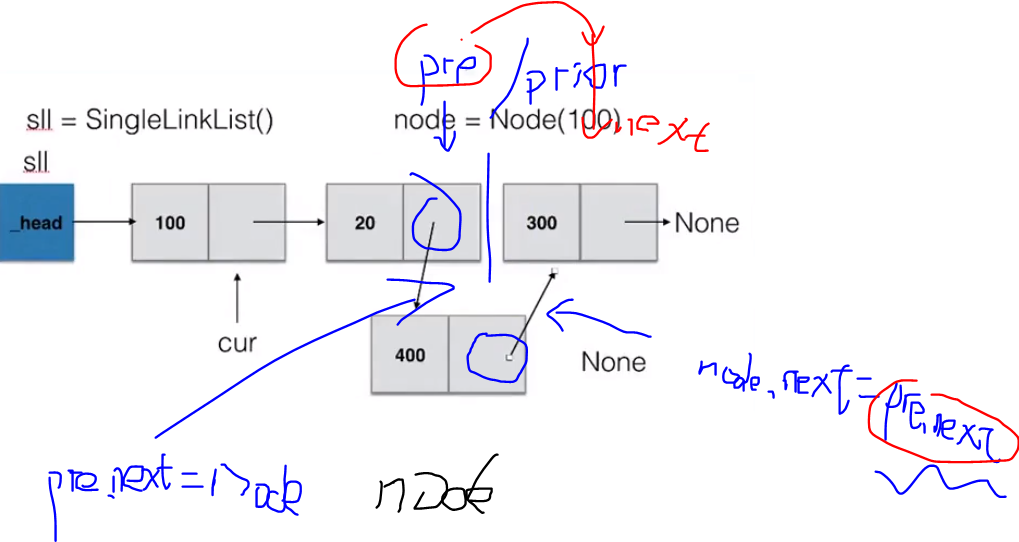
  def insert(self, pos, item):
        """指定位置添加元素"""
        # 若指定位置pos为第一个元素之前，则执行头部插入
        if pos <= 0:
            self.add(item)
        # 若指定位置超过链表尾部，则执行尾部插入
        elif pos > (self.length()-1):
            self.append(item)
        # 找到指定位置
        else:
            node = SingleNode(item)
            count = 0
            # pre用来指向指定位置pos的前一个位置pos-1，初始从头节点开始移动到指定位置
            pre = self._head
            while count < (pos-1):
                count += 1
                pre = pre.next
            # 当循环推出后，pre指向pos-1位置，先将新节点node的next指向插入位置的节点
            node.next = pre.next
            # 将插入位置的前一个节点的next指向新节点
            pre.next = node

3-07：单链表查找和删除元素

    def search(self,item):
        """链表查找节点是否存在，并返回True或者False"""
        cur = self._head
        while cur != None:
            if cur.item == item:
                return True
            cur = cur.next
        return False

删除元素

    def remove(self,item):
        """删除节点"""
        cur = self._head
        pre = None
        while cur != None:
            # 找到了指定元素
            if cur.item == item:
                # 如果第一个就是删除的节点
                if not pre:
                    # 将头指针指向头节点的后一个节点
                    self._head = cur.next
                else:
                    # 将删除位置前一个节点的next指向删除位置的后一个节点
                    pre.next = cur.next
                break
            else:
                # 继续按链表后移节点
                pre = cur
                cur = cur.next

 3-08：单链表与顺序表的对比

链表失去了顺序表随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大，但对存储空间的使用要相对灵活。

class Node(object):
    """节点"""
    def __init__(self, item):
        self.item = item
        self.next = None


class SinCycLinkedlist(object):
    """单向循环链表"""
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head == None

    def length(self):
        """返回链表的长度"""
        # 如果链表为空，返回长度0
        if self.is_empty():
            return 0
        count = 1
        cur = self._head
        while cur.next != self._head:
            count += 1
            cur = cur.next
        return count

    def travel(self):
        """遍历链表"""
        if self.is_empty():
            return
        cur = self._head
        print cur.item,
        while cur.next != self._head:
            cur = cur.next
            print cur.item,
        print ""


    def add(self, item):
        """头部添加节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
            node.next = self._head
        else:
            #添加的节点指向_head
            node.next = self._head
            # 移到链表尾部，将尾部节点的next指向node
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            cur.next = node
            #_head指向添加node的
            self._head = node

    def append(self, item):
        """尾部添加节点"""
        node = Node(item)
        if self.is_empty():
            self._head = node
            node.next = self._head
        else:
            # 移到链表尾部
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            # 将尾节点指向node
            cur.next = node
            # 将node指向头节点_head
            node.next = self._head

    def insert(self, pos, item):
        """在指定位置添加节点"""
        if pos <= 0:
            self.add(item)
        elif pos > (self.length()-1):
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            count = 0
            # 移动到指定位置的前一个位置
            while count < (pos-1):
                count += 1
                cur = cur.next
            node.next = cur.next
            cur.next = node

    def remove(self, item):
        """删除一个节点"""
        # 若链表为空，则直接返回
        if self.is_empty():
            return
        # 将cur指向头节点
        cur = self._head
        pre = None
        # 若头节点的元素就是要查找的元素item
        if cur.item == item:
            # 如果链表不止一个节点
            if cur.next != self._head:
                # 先找到尾节点，将尾节点的next指向第二个节点
                while cur.next != self._head:
                    cur = cur.next
                # cur指向了尾节点
                cur.next = self._head.next
                self._head = self._head.next
            else:
                # 链表只有一个节点
                self._head = None
        else:
            pre = self._head
            # 第一个节点不是要删除的
            while cur.next != self._head:
                # 找到了要删除的元素
                if cur.item == item:
                    # 删除
                    pre.next = cur.next
                    return
                else:
                    pre = cur
                    cur = cur.next
            # cur 指向尾节点
            if cur.item == item:
                # 尾部删除
                pre.next = cur.next

    def search(self, item):
        """查找节点是否存在"""
        if self.is_empty():
            return False
        cur = self._head
        if cur.item == item:
            return True
        while cur.next != self._head:
            cur = cur.next
            if cur.item == item:
                return True
        return False

if __name__ == "__main__":
    ll = SinCycLinkedlist()
    ll.add(1)
    ll.add(2)
    ll.append(3)
    ll.insert(2, 4)
    ll.insert(4, 5)
    ll.insert(0, 6)
    print "length:",ll.length()
    ll.travel()
    print ll.search(3)
    print ll.search(7)
    ll.remove(1)
    print "length:",ll.length()
    ll.travel()

算法是独立存在的一种解决问题的方法和思想。

时间复杂度的几条基本计算规则

• 基本操作，即只有常数项，认为其时间复杂度为O(1)
• 顺序结构，时间复杂度按加法进行计算
• 循环结构，时间复杂度按乘法进行计算
• 分支结构，时间复杂度取最大值
• 判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
• 在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度