核能国度 题解
题意
\(~~~~\) 给出 \(W \times H\) 的矩形,\(N\) 个修改,每个修改有位置及参数 \(a,b\) ,表示对其周边距离它切比雪夫距离为 \(d\) 的格子的权值增加 \(\max(0,a-b\times d)\) 。最后 \(Q\) 组询问,每次求一个子矩阵的和。
题解
\(~~~~\) 我不会告诉你我做这道题做了半个月并且实现还借助了题解。(虽然有一周在期末考试。
Solution 1 暴力
\(~~~~\) 每次暴力修改其影响到的格子的权值,每次查询暴力求子矩阵的和,这个不多说。
\(~~~~\) 期望得分:???
Solution 2 二维前缀和
\(~~~~\) 暴力修改权值后做一遍二维前缀和,每次查询 \(\mathcal{O}(1)\) 回答。
\(~~~~\) 期望得分:\(\texttt{25pts}\)
Solution 3 一维差分
\(~~~~\) 观察到有 \(\texttt{40pts}\) 给在 \(H=1\) ,那么此时整个矩形可以被看作是一排数。设某个横坐标为 \(x\) 的修改能影响到的最远的距离 \(\dfrac{a}{b}=d\) ,那么就相当于给 \([x-d,x]\) 加上一个首项为 \(a \bmod b\) ,公差为 \(b\) ;给 \([x+1,x+d]\) 加上一个首项为 \(a-b\) ,公差为 \(-b\) 的等差数列。
\(~~~~\) 此时套路地维护这个数列的差分数列,那么需要支持区间加法,单点修改,且询问在所有修改之后。因此用差分维护差分数列,还原后再用一维前缀和回答即可。
\(~~~~\) 期望得分:结合 Solution 2 可得 \(\texttt{50pts}\)(部分子任务重合)。
Solution 3.5 半个正解的二维差分
\(~~~~\) 你已经想到用差分维护一维差分数列了,那么我们来随便举个例子看二维的情况:
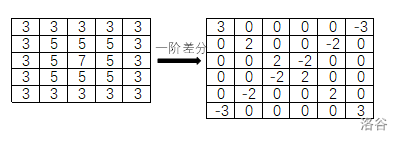
\(~~~~\) 这是一个 \(a=7,b=2\) 的例子,(虽然画错了),但不难看出在差分后的规律:
\(~~~~\bullet\) 左上和右下角为 \(a \bmod b\),右上和左下角为 \(- a \bmod b\) 。
\(~~~~\bullet\) 除开四角,主对角线全为 \(b\) ,副对角线全为 \(-b\) 。
\(~~~~\) 当然直接根据差分的式子也能得到这个规律,这里为了直观就用找规律了。
\(~~~~\) 那么我们暴力 (指 O(1)) 修改四角,然后差分维护对角线即可。
\(~~~~\) 时间复杂度:\(\mathcal{O}(N+WH+Q)\) 。
\(~~~~\) 期望得分:结合 Solution 2 和 Solution 3 可得 \(\texttt{75pts}\) 。
\(~~~~\) 这里贴一个我写了三次才写出来的仅能得新增的 \(\texttt{25pts}\) 的代码:
查看代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
const ll MAXN=2500005;
ll n,m,k,q;
struct Array{ll mp[50000000];inline ll* operator [] (const ll& x){return mp+(x+(n+1)+1)*(3*m+1);}}Pre,Dia1,Dia2;//用指针开数组
int main() {
scanf("%lld %lld %lld",&n,&m,&k);
while(k--)
{
ll x,y;ll a,b;
scanf("%lld %lld %lld %lld",&x,&y,&a,&b);
ll Up=a/b;
if(x-Up>0) Pre[x-Up][y-Up]+=a%b;Pre[x+Up+1][y+Up+1]+=a%b;
Pre[x+Up+1][y-Up]-=a%b;Pre[x-Up][y+Up+1]-=a%b;
Dia1[x-Up+1][y-Up+1]+=b;Dia1[x+Up+1][y+Up+1]-=b;
Dia2[x+Up][y-Up+1]-=b;Dia2[x-Up][y+Up+1]+=b;
}
for(ll j=1;j<=m;j++)
{
for(ll i=1;i<=n;i++)
{
Dia1[i][j]+=Dia1[i-1][j-1],Dia2[i][j]+=Dia2[i+1][j-1];
Pre[i][j]+=Dia1[i][j]+Dia2[i][j];
Pre[i][j]+=Pre[i-1][j]+Pre[i][j-1]-Pre[i-1][j-1];
}
}
for(ll j=1;j<=m;j++) for(ll i=1;i<=n;i++) Pre[i][j]+=Pre[i-1][j]+Pre[i][j-1]-Pre[i-1][j-1];
ll Q;scanf("%lld",&Q);
while(Q--)
{
ll X1,X2,Y1,Y2;
scanf("%lld %lld %lld %lld",&X1,&Y1,&X2,&Y2);
ll Siz=(Y2-Y1+1)*(X2-X1+1);
printf("%lld\n",(ll)((Pre[X2][Y2]-Pre[X1-1][Y2]-Pre[X2][Y1-1]+Pre[X1-1][Y1-1])*1.0/Siz+0.5));
}
return 0;
}
Solution 4 加了亿些细节的二维差分
\(~~~~\) 事实上 ,上面算法的时间复杂度是对的,但它并不能得全分。如果你仔细观察题目,你会看到这样一句话:
\(~~~~\) 如果核电站位于核能国的边境或是在离边境稍近的位置,那么爆炸可能也会影响到核能国之外的方格。影响到核能国外方格的爆炸被称作界限。
\(~~~~\) 而上面 Solution3.5 新增的 \(\texttt{25pts}\) 来自没有界限的子任务。仔细思考一下,我们会发现如果爆炸影响到的格子在当前矩形的左、左上或上方时,差分标记会影响内部的值,但如果出界了我们统计不到那部分。
\(~~~~\) 而且本题我们无法通过扩大若干倍矩形来强行统计那些部分,考虑一个极端情况:\(W=H=1\) ,然后在那个格子上有一个 \(a=2^{63},b=1\) 的修改。
\(~~~~\) 以下涉及大量代码实现,其中 \(n\),\(m\) 是题面中 \(W\) 和 \(H\)
\(~~~~\) 那么我们分别对每一种标记来考虑怎么处理出界的问题:
\(~~~~\) 对于四角的修改,我们强行移动它到对应的第一个生效的位置即可,换句话说就是把小于 \(1\) 的坐标移动到 \(1\) :
查看代码
void Tag(ll X1,ll Y1,ll X2,ll Y2,ll V)
{
S[X1][Y1]+=V;S[X2+1][Y1]-=V;
S[X1][Y2+1]-=V;S[X2+1][Y2+1]+=V;
}
Tag(max(x-Up,1ll),max(y-Up,1ll),min(x+Up,n),min(y+Up,m),a%b-b);//调用,注意后面即使对答案不影响也不能不取min,否则会RE。
// 最后对于四角-b,则整个对角线都+b即可
\(~~~~\) 对于主对角线的修改,我们将其超出部分的和全部移动到第一行或第一列对应的位置,这个需要分类讨论几种情况。
\(~~~~\) 先写一个给第一行/列打标记的函数:
查看代码
ll A[MAXN],B[MAXN];//记超出部分给 第一行 和 第一列 打的标记
void Sign(ll *Arr,ll l,ll r,ll v) {Arr[l]+=v,Arr[r+1]-=v;} //一阶差分,对 [l,r] +v ,记在第一行或第一列
\(~~~~\) 然后对超出的左上角部分进行处理:
查看代码
void TagLU(ll X1,ll Y1,ll X2,ll Y2,ll V)//[X1,Y1]:起始 [X2,Y2]:最后一个超出的格子
{
if(X1>X2)return;
if(X2<=0&&Y2<=0) Sign(A,1,1,(X2-X1+1)*V); // Area 1:全部在左上
else if(X2<=0)//Area 2:左
{
if(Y1<=0) Sign(B,1,Y2,V),Sign(B,1,1,(1-Y1)*V);//有一部分在左上
else Sign(B,Y1,Y2,V);//全在左
}
else if(Y2<=0)//Area 3:上
{
if(X1<=0) Sign(A,1,X2,V),Sign(A,1,1,(1-X1)*V);//有一部分在左上
else Sign(A,X1,X2,V);//全在上
}
}
TagLU(X-Up,Y-Up,X-min(min(X-1,Y-1),Up)-1,Y-min(min(X-1,Y-1),Up)-1,b);
\(~~~~\) 以及打起始和结束的标记:
查看代码
Dia1[X-min(min(X-1,Y-1),Up)][Y-min(min(X-1,Y-1),Up)]+=b;
Dia1[X+1+min(Up,min(n-X-1,m-Y))+1][Y+1+min(Up,min(n-X,m-Y-1))+1]-=b;
\(~~~~\) 然后是副对角线,大体同上,但注意左右都可能有超出。
查看代码
void TagRU(ll Y1,ll Y2,ll V){if(Y1>=Y2&&Y2<=m) Sign(B,Y2,min(Y1,m),-V);}
void TagLD(ll X1,ll X2,ll V){if(X1<=X2&&X1<=n) Sign(A,X1,min(X2,n),-V);}
void Tag(ll X,ll Y,ll a,ll b)
{
ll Up=a/b;
TagRU(Y+1+Up,Y+1+min(Up,min(X-1,m-Y-1))+1,b);
TagLD(X+1+min(Up,min(n-X-1,Y-1))+1,X+1+Up,b);
Dia2[X-min(Up,min(X-1,m-Y-1))][Y+1+min(Up,min(X-1,m-Y-1))]-=b;
Dia2[X+1+min(Up,min(n-X-1,Y-1))+1][Y-min(Up,min(n-X-1,Y-1))-1]+=b;
}
\(~~~~\) 最后把对角线的差分标记还原,把第一行和第一列归到一起
查看代码
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) Dia1[i][j]+=Dia1[i-1][j-1],Dia2[i][j]+=Dia2[i-1][j+1];
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) Dia1[i][j]+=Dia2[i][j];
for(int i=1;i<=n;i++) Dia1[i][1]+=(A[i]+=A[i-1]);
for(int i=1;i<=m;i++) Dia1[1][i]+=(B[i]+=B[i-1]);
\(~~~~\) 然后就和上面没有任何区别了。轻松而又愉快。
\(~~~~\) 时间复杂度:同 Solution3.5
\(~~~~\) 期望得分:\(\texttt{100pts}\) 。
\(~~~~\) 完整代码就不贴了,整体很丑。