挺简单的一套题,题型都见过,但是只有180分,T1的eps设的1e-12,直接T飞。
本来校内rk9,但是由于我前面的4个都同时炸了,所以现在是并列rk5。
T1
二分答案肯定能想到,关键在于如何check。
把式子列出来看下:
sum[R]-sum[L-1]>=x*(R-L+1);
sum[R]-x*R>=sum[L-1]-x*(L-1);
于是问题转化为了一个简单的逆序对问题,树状数组/分治即可
T2
直接说正解了:
设f[i][j]代表第i列选j个颜色的方案数,
g[i][j]代表用任意i个颜色填j个块的方案数,
h[i][j]代表上一列选i个颜色这一列选j个的方案数
g[i][j]=g[i-1][j-1]*(p-i+1)+g[i][j-1]*i;
h[j][k]= 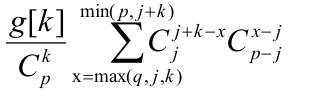 ;
;
f[i][j]=f[i-1][k]*h[k][j];
我们发现f的转移系数与i无关,所以可以用矩阵乘优化。
时间复杂度 $ O(n^3*log2(m)) $
T3
讲讲我的做法吧,很好理解:
首先第一问用主席树维护,
之后建一颗线段树,
接着把操作按W排序,对于每个操作L,R,W,
在树上对应的区间的vector存上这个W。
最后对于每个修改,在线段树上单点查询lower_bound即可
考场上两个板子都打对了我很kx