Problem Description
Somewhere deep in the Czech Technical University buildings, there are laboratories for examining mechanical and electrical properties of various materials. In one of yesterday’s presentations, you have seen how was one of the laboratories changed into a new multimedia lab. But there are still others, serving to their original purposes.
In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order.
Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B.
A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc.
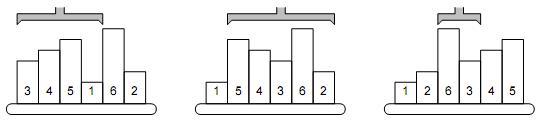
The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc.
Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.
In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order.
Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B.
A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc.

The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc.
Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.
Input
The input consists of several scenarios. Each scenario is described by two lines. The first line contains one integer number N , the number of samples, 1 ≤ N ≤ 100 000. The second line lists exactly N space-separated positive integers, they specify the heights of individual samples and their initial order.
The last scenario is followed by a line containing zero.
The last scenario is followed by a line containing zero.
Output
For each scenario, output one line with exactly N integers P1 , P1 , . . . PN ,separated by a space.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.
Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.
Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed.
Sample Input
6
3 4 5 1 6 2
4
3 3 2 1
0
Sample Output
4 6 4 5 6 6
4 2 4 4
Source
感觉是一个比较好(shui)的splay的练习题对于初学者来说,每次都是把最小值提到根节点,然后将左边区间打上rev标记,
每次splay或者是求前驱时再把标记下放。
我交了那么多次,居然都是pe,格式很重要qwq。
1 #include <algorithm> 2 #include <iostream> 3 #include <cstring> 4 #include <cstdio> 5 using namespace std; 6 const int N = 100000 + 11; 7 int n,root; 8 struct id 9 { 10 int num,idx; 11 bool operator < (const id &A) const 12 { 13 if(num == A.num) return idx < A.idx; 14 return num < A.num; 15 } 16 }nums[N]; 17 18 struct Splay_tree 19 { 20 int key,size,son[2],f,rev; 21 void clear() 22 { 23 key = son[0] = son[1] = f = size = rev = 0; 24 } 25 void news(int keys) 26 { 27 key = keys,size = 1, son[0] = son[1] = rev = f = 0; 28 } 29 30 } tree[N]; 31 32 int get(int x) 33 { 34 return x == tree[tree[x].f].son[1]; 35 } 36 37 void push_down(int now) 38 { 39 if(tree[now].rev == 1) 40 { 41 tree[now].rev = 0; 42 swap(tree[now].son[0],tree[now].son[1]); 43 for(int i = 0; i < 2; ++i)if(tree[now].son[i])tree[tree[now].son[i]].rev ^= 1; 44 } 45 } 46 47 void updata(int now) 48 { 49 tree[now].size = 1; 50 if(tree[now].son[0]) tree[now].size += tree[tree[now].son[0]].size; 51 if(tree[now].son[1]) tree[now].size += tree[tree[now].son[1]].size; 52 } 53 54 void ratote(int x) 55 { 56 int fa = tree[x].f;int gfa = tree[fa].f; 57 int ze = get(x); 58 tree[fa].son[ze] = tree[x].son[ze^1]; tree[tree[fa].son[ze]].f = fa; 59 tree[x].son[ze^1] = fa, tree[fa].f = x; tree[x].f = gfa; 60 ze = (fa == tree[gfa].son[1]); 61 if( gfa ) 62 tree[gfa].son[ze] = x; 63 updata(fa); updata(x); 64 } 65 66 67 int c[N],tot; 68 void finds(int num) 69 { 70 tot = 1; int now = num; 71 c[1] = num; 72 while(tree[now].f) 73 { 74 c[++tot] = tree[now].f; 75 now = tree[now].f; 76 } 77 for(int i = tot; i > 0; --i) push_down(c[i]); 78 } 79 80 void splay(int x) 81 { 82 finds(x); 83 for(int i; i = tree[x].f; ratote(x)) 84 { 85 86 if(tree[i].f) 87 if(get(i) == get(x)) ratote(i); 88 } 89 root = x; 90 } 91 92 void insert(int idx,int num) 93 { 94 if(root == 0){tree[idx].news(num),root = idx;return;} 95 int now = root,fa = now; 96 while(1) 97 { 98 int ze = num > tree[now].key; 99 fa = now; now = tree[fa].son[ze]; 100 if(!now) 101 { 102 tree[idx].news(num); tree[idx].f = fa; 103 tree[fa].son[ze] = idx; 104 updata(fa); splay(idx); return; 105 } 106 } 107 } 108 109 int pre(int now) 110 { 111 now = tree[now].son[0]; 112 while(1) 113 { 114 push_down(now); 115 if(!tree[now].son[1])return now; 116 now = tree[now].son[1]; 117 } 118 } 119 120 void del(int x) 121 { 122 if(!tree[root].son[0] && !tree[root].son[1]) {root = 0; tree[root].clear(); return;} 123 if(!tree[root].son[1] || !tree[root].son[0]) 124 { 125 int ze = !tree[root].son[1]; 126 int root_y = root; root = tree[root].son[ze^1]; 127 tree[root_y].clear(); tree[root].f = 0; return; 128 } 129 int pres = pre(root);int root_y = root; 130 splay(pres); 131 tree[pres].son[1] = tree[root_y].son[1]; 132 tree[tree[pres].son[1]].f = pres; 133 tree[root_y].clear(); updata(pres); 134 135 } 136 137 void Init() 138 { 139 for(int i = 1; i <= n; ++i) 140 { 141 scanf("%d",&nums[i].num); 142 nums[i].idx = i; 143 insert(i,i); 144 } 145 sort(nums + 1, nums + 1 + n); 146 } 147 148 149 150 void Solve() 151 { 152 for(int x = 1; x < n; ++x) 153 { 154 splay(nums[x].idx); 155 push_down(root); 156 int ans = x; 157 if(tree[root].son[0]) ans += tree[tree[root].son[0]].size; 158 printf("%d ",ans); 159 tree[tree[root].son[0]].rev ^= 1; 160 del(nums[x].idx); 161 } 162 printf("%d ",n); 163 164 } 165 166 int main() 167 { 168 while(~scanf("%d",&n)&&n) 169 { 170 root = 0; memset(tree,0,sizeof(tree)); 171 Init(); 172 Solve(); 173 } 174 return 0; 175 }