算法复习——左偏树

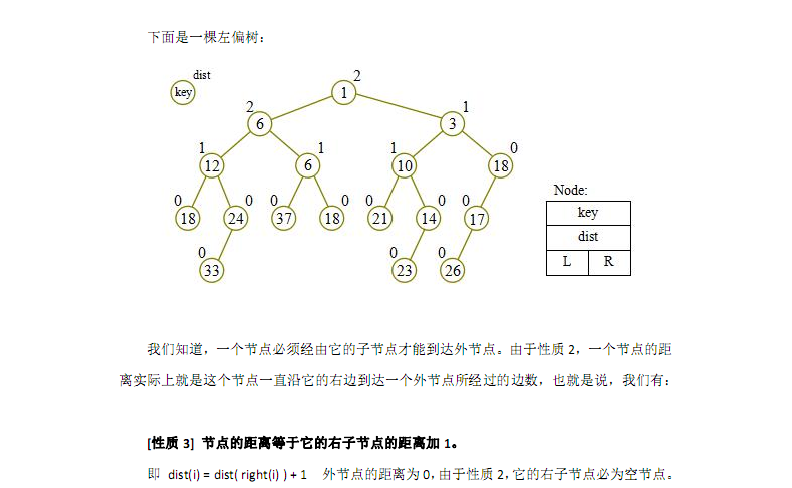
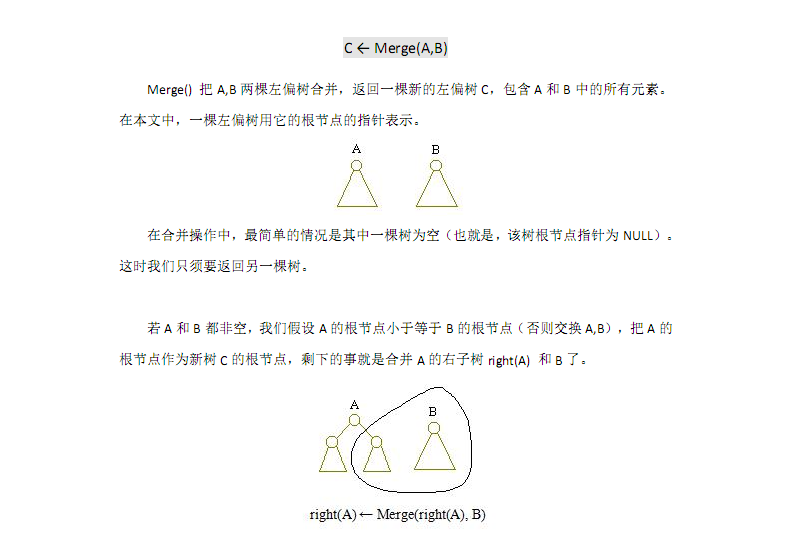
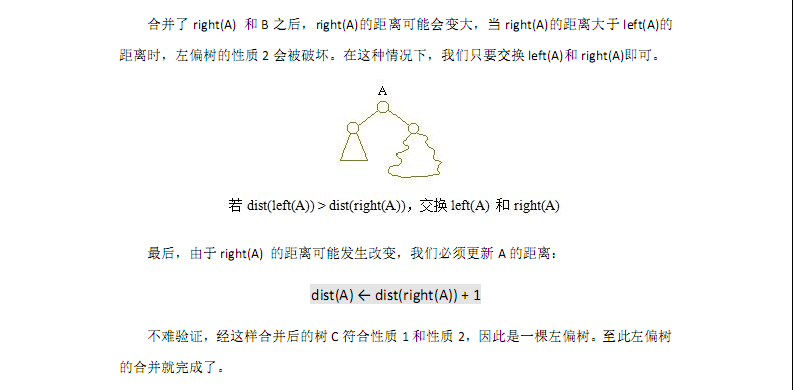
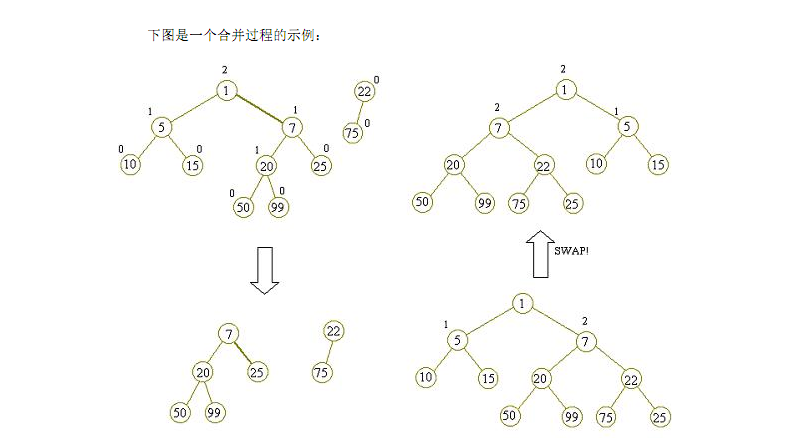
搬讲义

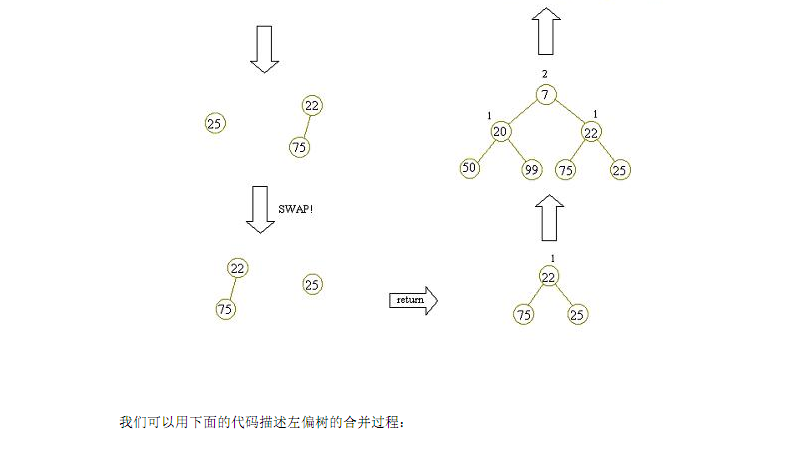
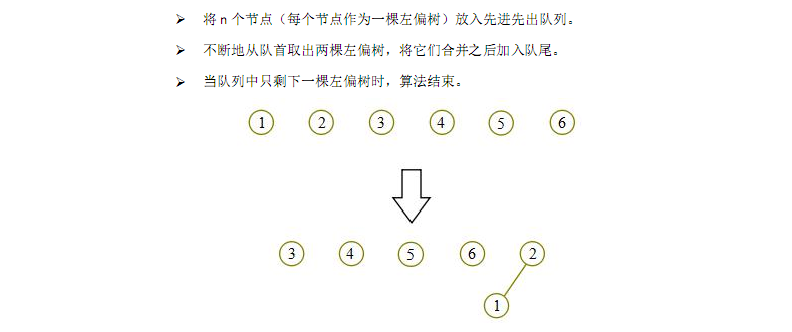
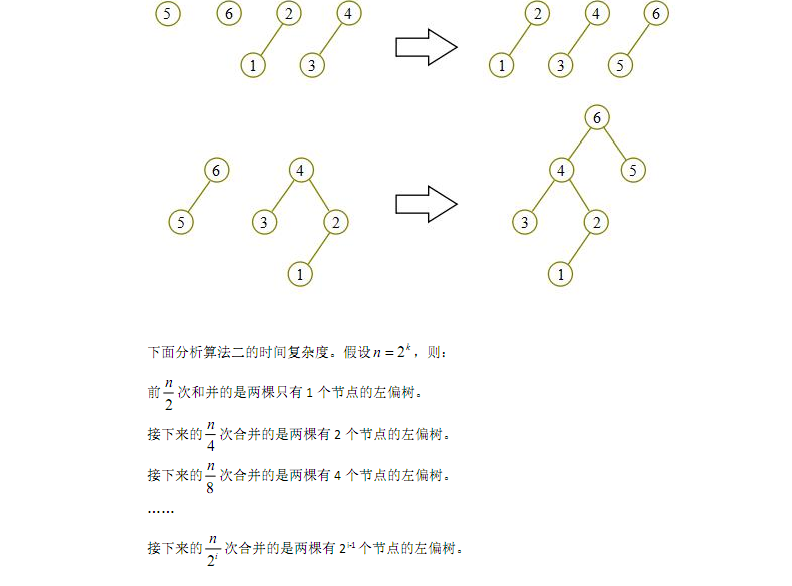
最后删除已知节点的操作我就不搬了···因为如果要执行这种操作了还不如用splay之类的平衡树······

例题1（罗马游戏 bzoj1455）：

Description

罗马皇帝很喜欢玩杀人游戏。 他的军队里面有n个人，每个人都是一个独立的团。最近举行了一次平面几何测试，每个人都得到了一个分数。 皇帝很喜欢平面几何，他对那些得分很低的人嗤之以鼻。他决定玩这样一个游戏。 它可以发两种命令： 1. Merger(i, j)。把i所在的团和j所在的团合并成一个团。如果i, j有一个人是死人，那么就忽略该命令。 2. Kill(i)。把i所在的团里面得分最低的人杀死。如果i这个人已经死了，这条命令就忽略。 皇帝希望他每发布一条kill命令，下面的将军就把被杀的人的分数报上来。（如果这条命令被忽略，那么就报0分）

Input

第一行一个整数n（1<=n<=1000000）。n表示士兵数，m表示总命令数。 第二行n个整数，其中第i个数表示编号为i的士兵的分数。（分数都是[0..10000]之间的整数） 第三行一个整数m(1<=m<=100000) 第3+i行描述第i条命令。命令为如下两种形式： 1. M i j 2. K i

Output

如果命令是Kill，对应的请输出被杀人的分数。（如果这个人不存在，就输出0）

Sample Input

5
100 90 66 99 10
7
M 1 5
K 1
K 1
M 2 3
M 3 4
K 5
K 4

Sample Output

10
100
0
66

 

模板题····删除最小节点与合并操作···

注意每个堆的根节点用并查集维护····

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=1000005;
struct node
{
  int l,r,dis,val,fa;
  bool ifdead;
}p[N];
int n,m;
inline int R()
{
  char c;int f=0;
  for(c=getchar();c<'0'||c>'9';c=getchar());
  for(;c<='9'&&c>='0';c=getchar())
    f=(f<<3)+(f<<1)+c-'0';
  return f;
}
inline int getfa(int a)
{
  if(p[a].fa==a)  return a;
  else return p[a].fa=getfa(p[a].fa);
}
inline int merge(int a,int b)
{
  if(!a)  return b;
  if(!b)  return a;
  if(p[a].val>p[b].val)  swap(a,b);
  p[a].r=merge(p[a].r,b);
  if(p[p[a].r].dis>p[p[a].l].dis)  swap(p[a].l,p[a].r);
  p[a].dis=p[p[a].r].dis+1;
  return a;
}
int main()
{
  //freopen("a.in","r",stdin);
  n=R();char s[5];int a,b;
  for(int i=1;i<=n;i++)
    p[i].val=R(),p[i].fa=i;
  m=R();  
  while(m--)
  {
    scanf("%s",s);a=R();
    if(s[0]=='M')
    {
      b=R();
      if(p[a].ifdead||p[b].ifdead)  continue;
      int faa=getfa(a),fab=getfa(b);
      if(faa==fab)  continue;
      int t=merge(faa,fab);
      p[faa].fa=p[fab].fa=t;
    }
    if(s[0]=='K')
    {
      if(p[a].ifdead)  
      {
        printf("0
");continue;
      }
      int t=getfa(a);
      printf("%d
",p[t].val);
      p[t].ifdead=true;
      p[t].fa=merge(p[t].l,p[t].r);
      p[p[t].fa].fa=p[t].fa;
    }
  }
  return 0;
}

例题2：dispatching（bzoj2809）

Description

在一个忍者的帮派里，一些忍者们被选中派遣给顾客，然后依据自己的工作获取报偿。在这个帮派里，有一名忍者被称之为 Master。除了 Master以外，每名忍者都有且仅有一个上级。为保密，同时增强忍者们的领导力，所有与他们工作相关的指令总是由上级发送给他的直接下属，而不允许通过其他的方式发送。现在你要招募一批忍者，并把它们派遣给顾客。你需要为每个被派遣的忍者 支付一定的薪水，同时使得支付的薪水总额不超过你的预算。另外，为了发送指令，你需要选择一名忍者作为管理者，要求这个管理者可以向所有被派遣的忍者 发送指令，在发送指令时，任何忍者（不管是否被派遣）都可以作为消息的传递 人。管理者自己可以被派遣，也可以不被派遣。当然，如果管理者没有被排遣，就不需要支付管理者的薪水。你的目标是在预算内使顾客的满意度最大。这里定义顾客的满意度为派遣的忍者总数乘以管理者的领导力水平，其中每个忍者的领导力水平也是一定的。写一个程序，给定每一个忍者 i的上级 Bi，薪水Ci，领导力L i，以及支付给忍者们的薪水总预算 M，输出在预算内满足上述要求时顾客满意度的最大值。

 

1  ≤N ≤ 100,000 忍者的个数；

1  ≤M ≤ 1,000,000,000 薪水总预算； 

 

0  ≤Bi < i  忍者的上级的编号；

1  ≤Ci ≤ M                     忍者的薪水；

1  ≤Li ≤ 1,000,000,000             忍者的领导力水平。

Input

从标准输入读入数据。

 

第一行包含两个整数 N和 M，其中 N表示忍者的个数，M表示薪水的总预算。

 

接下来 N行描述忍者们的上级、薪水以及领导力。其中的第 i 行包含三个整 Bi , C i , L i分别表示第i个忍者的上级，薪水以及领导力。Master满足B i = 0，并且每一个忍者的老板的编号一定小于自己的编号 Bi < i。

Output

输出一个数，表示在预算内顾客的满意度的最大值。

Sample Input

5 4
0 3 3
1 3 5
2 2 2
1 2 4
2 3 1

Sample Output

6

先说下大概思路，维护每一个节点所在子树的大根堆···如果堆的总和超过m就弹出堆顶元素···然后更新答案,我们肯定不能每次枚举一个节点暴力构堆,因此我们dfs，每df完一个节点的儿子将儿子的大根堆加入到该节点的大根堆中·····

值得注意的是，一个节点的大根堆里可能并不包含该节点，因为有可能该节点并没有取，但为了方便维护，我们用fa[i]表示一个节点的所在子树部分元素组成的大根堆的堆顶元素···而不是表示i节点所在大根堆的堆顶元素······下面代码中的sum[i],size[i]同理

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<algorithm>
#include<string>
using namespace std;
const int N=1e5+5;
struct node
{
  int ls,rs,dis,c;
}p[N];
int n,m,first[N],go[N*2],next[N*2],tot,root,fa[N],size[N],sum[N],l[N],val[N];
long long ans;
inline int R()
{
  char c;int f=0;
  for(c=getchar();c<'0'||c>'9';c=getchar());
  for(;c<='9'&&c>='0';c=getchar())
    f=(f<<3)+(f<<1)+c-'0';
  return f;
}
inline int getfa(int a)
{
  if(fa[a]==a)  return a;
  else return fa[a]=getfa(fa[a]);
}
inline void comb(int a,int b)
{
  next[++tot]=first[a],first[a]=tot,go[tot]=b;
  next[++tot]=first[b],first[b]=tot,go[tot]=a; 
}
inline int merge(int a,int b)
{
  if(!a)  return b;
  if(!b)  return a;
  if(p[a].c<p[b].c)  swap(a,b);
  p[a].rs=merge(p[a].rs,b);
  if(p[p[a].rs].dis>p[p[a].ls].dis)  swap(p[a].ls,p[a].rs);
  p[a].dis=p[p[a].rs].dis+1;
  return a;
}
inline void pop(int u)
{
  int t=fa[u];
  fa[u]=merge(p[t].ls,p[t].rs);
  size[u]--;sum[u]-=p[t].c;
  p[t].c=p[t].ls=p[t].rs=0;
}
inline void dfs(int u,int pre)
{
  for(int e=first[u];e;e=next[e])
  {
    int v=go[e];
    if(v==pre)  continue;
    dfs(v,u);
    size[u]+=size[v],sum[u]+=sum[v];
    fa[u]=fa[v]=merge(fa[u],fa[v]);
    while(sum[u]>m)  pop(u);    
  }
  size[u]+=1;sum[u]+=val[u];
  p[u].c=val[u];fa[u]=merge(fa[u],u);
  while(sum[u]>m)  pop(u);
  ans=max(ans,(long long)size[u]*l[u]);
}
int main()
{
  //freopen("a.in","r",stdin);
  n=R(),m=R();int a;
  for(int i=1;i<=n;i++) 
  {
    a=R(),val[i]=R(),l[i]=R();
    if(!a)  root=i;
    else comb(a,i);
  }
  dfs(root,0);
  cout<<ans<<endl;
  return 0;
}

例题3：monkey king（hdu1512）

Problem Description

Once in a forest, there lived N aggressive monkeys. At the beginning, they each does things in its own way and none of them knows each other. But monkeys can't avoid quarrelling, and it only happens between two monkeys who does not know each other. And when it happens, both the two monkeys will invite the strongest friend of them, and duel. Of course, after the duel, the two monkeys and all of there friends knows each other, and the quarrel above will no longer happens between these monkeys even if they have ever conflicted.

Assume that every money has a strongness value, which will be reduced to only half of the original after a duel(that is, 10 will be reduced to 5 and 5 will be reduced to 2).

And we also assume that every monkey knows himself. That is, when he is the strongest one in all of his friends, he himself will go to duel.

Input

There are several test cases, and each case consists of two parts.

First part: The first line contains an integer N(N<=100,000), which indicates the number of monkeys. And then N lines follows. There is one number on each line, indicating the strongness value of ith monkey(<=32768).

Second part: The first line contains an integer M(M<=100,000), which indicates there are M conflicts happened. And then M lines follows, each line of which contains two integers x and y, indicating that there is a conflict between the Xth monkey and Yth

Output

For each of the conflict, output -1 if the two monkeys know each other, otherwise output the strongness value of the strongest monkey in all friends of them after the duel.

Sample Input

5 20 16 10 10 4 5 2 3 3 4 3 5 4 5 1 5

Sample Output

8 5 5 -1 10

 

这道题口糊起来听tm简单的···每一拨猴子直接维护一个大根堆···每次打架就是找到两个堆的堆顶先删除对顶···值除以2后再合并就可以了···

然而左偏树最蛋疼的地方就是那个father··通常既维护了并差集又维护每个点所在堆的对顶··然而这里如果有删除操作就不好搞了··要注意许多细节··详细见代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=1e5+5;
struct node
{
  int l,r,dis,val,fa;
}p[N];
int n,m;
inline int R()
{
  char c;int f=0;
  for(c=getchar();c<'0'||c>'9';c=getchar());
  for(;c<='9'&&c>='0';c=getchar())
    f=(f<<3)+(f<<1)+c-'0';
  return f;
} 
inline int getfa(int u)
{
  if(p[u].fa==u)  
    return u;
  else return p[u].fa=getfa(p[u].fa);
}
inline int merge(int a,int b)
{
  if(!(a*b))  return a+b;
  if(p[a].val<p[b].val)  swap(a,b);
  p[a].r=merge(p[a].r,b);p[p[a].r].fa=a;//细节1
  if(p[p[a].r].dis>p[p[a].l].dis)  swap(p[a].r,p[a].l);
  p[a].dis=p[p[a].r].dis+1;
  return a;
}
inline int change(int a,int b)
{
  p[p[a].l].fa=p[a].l;p[p[a].r].fa=p[a].r;  //细节2
  int tmp1=merge(p[a].l,p[a].r);
  p[a].val/=2;p[a].l=p[a].r=0;p[a].dis=0;
  int t1=merge(a,tmp1);
  p[p[b].l].fa=p[b].l;p[p[b].r].fa=p[b].r; //细节3
  int tmp2=merge(p[b].l,p[b].r);
  p[b].val/=2;p[b].l=p[b].r=0;p[b].dis=0;
  int t2=merge(b,tmp2);
  return merge(t1,t2);
}
int main()
{
  //freopen("a.in","r",stdin);
  while(scanf("%d",&n)!=EOF)
  {
    int a,b;
    for(int i=1;i<=n;i++)
      p[i].val=R(),p[i].fa=i,p[i].dis=p[i].l=p[i].r=0;
    m=R();
    while(m--)
    {
      a=R(),b=R();
      int faa=getfa(a),fab=getfa(b);
      if(faa==fab)  
      {    
        printf("-1
");continue;
       }
      int t=change(faa,fab);
      printf("%d
",p[t].val);
    }
  }
  return 0;
}