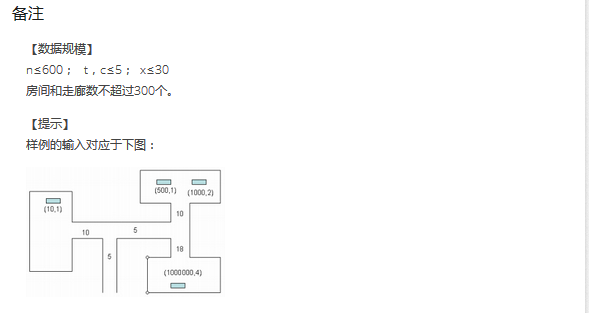
树形dp的状态转移分为两种,一种为从子节点到父节点,一种为父节点到子节点,下面主要讨论子节点到父亲节点的情况:
例题1(战略游戏):

这是一道典型的由子节点状态转移到父节点的问题,而且兄弟节点之间没有相互影响,我们用f[i][0]/f[i][1]表示i不取/要取时其所在子树总共最少取的节点数,不难得出dp方程:
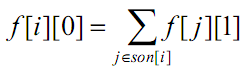

代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<cstring> #include<string> #include<algorithm> #include<cstdio> #include<cstdlib> #include<vector> using namespace std; const int N=1505; int first[N],next[N*2],go[N*2],tot,n,father[N],f[N][2]; vector<int>son[N]; inline int R() { char c;int f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f; } inline void comb(int a,int b) { next[++tot]=first[a],first[a]=tot,go[tot]=b; next[++tot]=first[b],first[b]=tot,go[tot]=a; } inline void dfs(int u,int fa) { for(int e=first[u];e;e=next[e]) { int v=go[e]; if(v==fa) continue; father[v]=u; son[u].push_back(v); dfs(v,u); } } inline void dp(int u) { int temp=1e+8; if(!son[u].size()) { f[u][0]=0;f[u][1]=1; return; } for(int i=0;i<son[u].size();i++) { dp(son[u][i]); f[u][0]+=f[son[u][i]][1]; f[u][1]+=min(f[son[u][i]][1],f[son[u][i]][0]); } f[u][1]++; } int main() { //freopen("a.in","r",stdin); int a,b,c; n=R(); for(int i=1;i<=n;i++) { a=R(),b=R(); for(int j=1;j<=b;j++) c=R(),comb(a,c); } dfs(0,0);dp(0); int ans=min(f[0][1],f[0][0]); cout<<ans<<endl; return 0; }
通过这道题我们也可以看出,如果兄弟节点间并不存在相互影响制约的关系,dp的第二维通常是非常小的
那么当兄弟节点间会相互影响时,又该怎么办,我们先讨论较为简单的二叉树的情况:
例题2(二叉苹果树):

首先将保留树枝数量转化成保留节点数量+1,(不转化也可以),然后每个树枝上的苹果数量设为相应节点的点权,我们发现,如果用f[i][k]表示i所在子树总共留下了k个节点,由于儿子节点只有两个,我们就可以枚举左儿子保留的节点数量x,则右儿子即为k-x-1,推出dp方程:
f[i][k]=max{f[lson][x]+f[rson][k-x-1],f[i][k]},0<=x<k
代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<cstring> #include<string> #include<algorithm> using namespace std; const int N=105; int first[N],next[N*2],go[N*2],val[N*2],tot; int n,m; int dp[N][N]; inline void comb(int a,int b,int c) { next[++tot]=first[a],first[a]=tot,go[tot]=b,val[tot]=c; next[++tot]=first[b],first[b]=tot,go[tot]=a,val[tot]=c; } inline void dfs(int u,int fa,int Val,int k) { if(u==0||k==0) { dp[u][k]=0; return; } if(dp[u][k]!=-1) return; dp[u][k]=0; for(int i=0;i<k;i++) { int l=0,r=0,vl,vr; for(int e=first[u];e;e=next[e]) { int v=go[e]; if(v==fa) continue; if(l==0) l=v,vl=val[e]; else { r=v,vr=val[e]; break; } } dfs(l,u,vl,i); dfs(r,u,vr,k-i-1); dp[u][k]=max(dp[l][i]+dp[r][k-i-1]+Val,dp[u][k]); } return; } int main() { //freopen("a.in","r",stdin); scanf("%d%d",&n,&m); m++; memset(dp,-1,sizeof(dp)); int a,b,c; for(int i=1;i<n;i++) { scanf("%d%d%d",&a,&b,&c); comb(a,b,c); } dfs(1,0,0,m); cout<<dp[1][m]<<endl; return 0; }
通过这道题,我们可以发现,如果兄弟节点间存在着相互影响的情况,那么常常会在dfs之前枚举儿子状态,保证儿子的状态不冲突,由于枚举会出现重复的情况,我们也常常会用到记忆化搜索
上面只是两个儿子的情况,如果面对多个儿子,上面的方法显然是不可取的
例题3(选课):
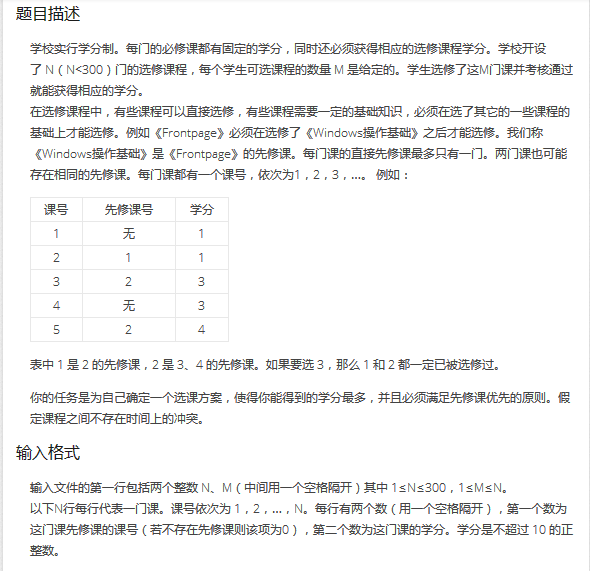
根据题意由先修课向它的课程连边,建成一颗树,树的点权对应课程学分
此时我们必须将多叉树转化为二叉树:把第一个孩子作为父节点的左子树,其它孩子作为第一个孩子的右子树。
具体实现为:每次读入一个节点i的儿子j,我们将son[i]=j,而将brother[j]设为之前的son[i],也就是离j最近的兄弟节点。
设f[u][k]为新建的二叉树的后,节点u所在子树保留k个儿子能得到得最多学分,可以得出dp方程:
f[u][k]=max(f[u][k],f[son[u]][i]+dp[brother[u]][k-i-1]+val[u]),0<=i<k;
其中val表示该节点对应课程的的学分
由实际意义不难发现,我们这样枚举少考虑了一个情况,也就是当前u节点所对应的原来的图的子树的节点都不取的情况,
因此在最后我们还要这样:
f[u][k]=max(f[u][k],f[brother[u]][k])
多叉树转二叉树的方法是面对分配附加维时常用的一种方法
例题4(偷天换日,洛谷3360):
首先要考虑的是这道题的建图,如果根据题意新建一个图是在太麻烦,因此我们可以直接考虑边读入信息边再已知的树上dfs,(详细见代码)
用f[i][j]表示已i为节点的子树(包含i与其父亲连接的边)中花费j的时间能获得的最大价值
当我们dfs到展览室的时候,f[i][j]的计算无疑是一个01背包问题,在此不多叙述
其他情况我们可以发现,除去末端展览室的情况,树的其他部分都是一颗二叉树,因此直接用我们上面提到的方法即可:
f[x][i]=max(f[x][i],f[l][j]+f[r][i-j-dis]);dis<=i<=n,j<=i-dis;
其中dis表示i与其父节点连接的边的权值;
代码如下:(引用洛谷题解)
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define ll long long ll n,m=1; ll f[1001][1001]={0}; ll value[1001],tim[1001]; inline void sca(ll x) { ll dis,pd; scanf("%lld%lld",&dis,&pd); dis*=2; if(pd) { for(ll j=1;j<=pd;j++) scanf("%lld%lld",&value[j],&tim[j]); for(ll i=1;i<=pd;i++) for(ll j=n;j>=tim[i];j--) if(j-tim[i]>=dis) f[x][j]=max(f[x][j],f[x][j-tim[i]]+value[i]); return; } ll l=++m;sca(m); ll r=++m;sca(m); for(ll i=dis;i<=n;i++) for(ll j=0;j<=i-dis;j++)f[x][i]=max(f[x][i],f[l][j]+f[r][i-j-dis]); } int main() { scanf("%lld",&n);n--; sca(1); printf("%lld",f[1][n]); return 0; }
例题5(骑士,bzoj1040):

首先想到的是如果按照痛恨关系建边的话有两种情况:有一个环或者为一颗树,为树的话就和例题1一样了,十分简单,因此主要考虑有环的情况.
为了让环更好处理,我们选择从被痛恨者向痛恨他的人连一条边····这样整个图即为奇环外向树(只有一个环且没有环外的点指向环内的点的图)
这样的话我们可以找环上任意一点u让它与它的父节点father[u]断开,然后以它为根进行dp,dp方程与例题1一样。
然而这样会出现冲突,因为最优答案有可能是由f[father[u]][1]更新过来的,因此我们要将环上的的点单独处理
首先直接将f[father[u]][1]赋值为f[father[u]][0]这样的话可以保证u取了而father[u]一定没有取,然后依次往father[father[u]],father[father[father[u]]]·····跳,即重新遍历整个环,依次更新遍历的点的f[][0],f[][1],直到跳到u为止
最后只更新f[u][1]就好了,ans加上max{f[u][1],f[u][0]}.
代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<cstring> #include<string> #include<algorithm> using namespace std; const int N=1e6+3; int first[N],next[N],go[N],tot,n,val[N],father[N],g[N]; long long ans=0,f[N][2]; bool visit[N]; inline int R() { char c;int f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f; } inline void comb(int a,int b) { next[++tot]=first[a],first[a]=tot,go[tot]=b; } inline void dfs(int u) { visit[u]=true;f[u][1]=val[u]; for(int e=first[u];e;e=next[e]) { int v=go[e]; if(!visit[v]) { dfs(v); f[u][0]+=max(f[v][0],f[v][1]); f[u][1]+=f[v][0]; } } } inline void dp(int a) { int root; for(root=a;g[root]!=a;root=father[root]) g[root]=a; dfs(root); int b=father[root]; f[b][1]=f[b][0]; for(int x=father[b];x!=root;x=father[x]) { f[x][1]=val[x],f[x][0]=0; for(int e=first[x];e;e=next[e]) { int v=go[e]; f[x][0]+=max(f[v][0],f[v][1]); f[x][1]+=f[v][0]; } } f[root][1]=val[root]; for(int e=first[root];e;e=next[e]) { int v=go[e]; f[root][1]+=f[v][0]; } ans+=max(f[root][1],f[root][0]); } int main() { //freopen("a.in","r",stdin); n=R();int a,b; for(int i=1;i<=n;i++) { a=R(),b=R(); val[i]=a,comb(b,i); father[i]=b; } for(int i=1;i<=n;i++) if(!visit[i]) dp(i); printf("%lld",ans); return 0; }
例题6(bzoj1023仙人掌)
Description
如果某个无向连通图的任意一条边至多只出现在一条简单回路(simple cycle)里,我们就称这张图为仙人掌
图(cactus)。所谓简单回路就是指在图上不重复经过任何一个顶点的回路。

举例来说,上面的第一个例子是一张仙人图,而第二个不是——注意到它有三条简单回路:(4,3,2,1,6
,5,4)、(7,8,9,10,2,3,7)以及(4,3,7,8,9,10,2,1,6,5,4),而(2,3)同时出现在前两
个的简单回路里。另外,第三张图也不是仙人图,因为它并不是连通图。显然,仙人图上的每条边,或者是这张仙
人图的桥(bridge),或者在且仅在一个简单回路里,两者必居其一。定义在图上两点之间的距离为这两点之间最
短路径的距离。定义一个图的直径为这张图相距最远的两个点的距离。现在我们假定仙人图的每条边的权值都是1
,你的任务是求出给定的仙人图的直径。
Input
输入的第一行包括两个整数n和m(1≤n≤50000以及0≤m≤10000)。其中n代表顶点个数,我们约定图中的顶
点将从1到n编号。接下来一共有m行。代表m条路径。每行的开始有一个整数k(2≤k≤1000),代表在这条路径上
的顶点个数。接下来是k个1到n之间的整数,分别对应了一个顶点,相邻的顶点表示存在一条连接这两个顶点的边
。一条路径上可能通过一个顶点好几次,比如对于第一个样例,第一条路径从3经过8,又从8返回到了3,但是我们
保证所有的边都会出现在某条路径上,而且不会重复出现在两条路径上,或者在一条路径上出现两次。
Output
只需输出一个数,这个数表示仙人图的直径长度。
Sample Input
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
5 2 14 9 15 10 8
10 1
10 1 2 3 4 5 6 7 8 9 10
Sample Output
9
HINT
对第一个样例的说明:如图,6号点和12号点的最短路径长度为8,所以这张图的直径为8。

这道题不得不说是真tm难啊····
题解详见:http://z55250825.blog.163.com/blog/static/150230809201412793151890/
说说我理解的吧····先进行一遍dfs造一颗树用f[i]表示从i往深处的链能到达的最大距离,注意是链,不是环·····,那么用这个尝试更新答案,(用u的儿子的f的次大值和最大值的和+1来更新)
然后我们要讨论的就是如何处理环上的情况····
对于环的话我们找到环上深度最高的点u,我们要按照f的定义求出f[u],(这里有点难想,设i为环上除u外的点,那么我们可以推出f[u]=max{f[i]+dis(u,i)},于是以后dfs到环上的话答案一定由f[u]更新而来
接下来我们就要解决如何算f[u],并且在更新答案时我们还忽略了环上的点可以更新答案,打个比方,如果环上有两个点i,j,那么答案可能由f[i]+f[j]+dis(i,j)更新而来·····
我们要先提取出这个环,然后利用单调队列来求这个东西····具体实现看代码吧,···大概有点类似于烽火传递····队列首与队列尾的距离不能大于环长度的一半(不然就不是最短距离),然后还要保持一个单调性···
代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<ctime> #include<cctype> #include<cstring> #include<string> #include<algorithm> using namespace std; const int N=5e4+5; int n,m,k,f[N],low[N],dfn[N],cnt,deep[N],father[N],tol; int first[N],go[N*10],next[N*10],tot,ans=0,queue[N*2],a[N*2]; inline int R() { char c;int f=0; for(c=getchar();c<'0'||c>'9';c=getchar()); for(;c<='9'&&c>='0';c=getchar()) f=(f<<3)+(f<<1)+c-'0'; return f; } void comb(int a,int b) { next[++tot]=first[a],first[a]=tot,go[tot]=b; next[++tot]=first[b],first[b]=tot,go[tot]=a; } void init() { n=R(),m=R();int a,b; while(m--) { k=R();a=R(); for(int i=1;i<k;i++) b=R(),comb(a,b),a=b; } } void dp(int root,int u) { int tail=1,head=1;tol=deep[u]-deep[root]+1; for(int i=u;i!=root;i=father[i]) a[tol--]=f[i]; a[tol]=f[root],tol=deep[u]-deep[root]+1; for(int i=tol+1;i<=tol*2;i++) a[i]=a[i-tol]; queue[head]=1; for(int i=2;i<=tol+tol/2;i++) { while(head<=tail&&queue[head]<i-tol/2) head++; ans=max(ans,a[queue[head]]+a[i]+i-queue[head]); while(head<=tail&&a[queue[tail]]-queue[tail]<=a[i]-i) tail--; queue[++tail]=i; } for(int i=2;i<=tol;i++) f[root]=max(f[root],a[i]+min(i-1,tol-i+1)); } void tarjan(int u) { low[u]=dfn[u]=++cnt; for(int e=first[u];e;e=next[e]) { int v=go[e]; if(father[u]==v) continue; if(!dfn[v]) father[v]=u,deep[v]=deep[u]+1,tarjan(v); low[u]=min(low[v],low[u]); if(dfn[u]<low[v]) ans=max(ans,f[u]+f[v]+1),f[u]=max(f[u],f[v]+1); } for(int e=first[u];e;e=next[e]) { int v=go[e]; if(father[v]!=u&&dfn[u]<dfn[v]) dp(u,v); } } int main() { //freopen("a.in","r",stdin); init(); tarjan(1); printf("%d ",ans); return 0; }