各类算法与性能分析
排序算法概论
1.冒泡排序O(n2 ):

public class BubbleSort{
public static int[] sort (int[] array){
if(array.length == 0){
return array;
}
for(int i=0;i<array.length;i++){
for(int j=0;j<array.length-1-i;j++){
if(array[j+1]<array[j]){
int temp = array[j+1];
array[j+1] = array[j];
array[j] = temp;
}
}
}
}
}
2.简单选择排序O(n2)
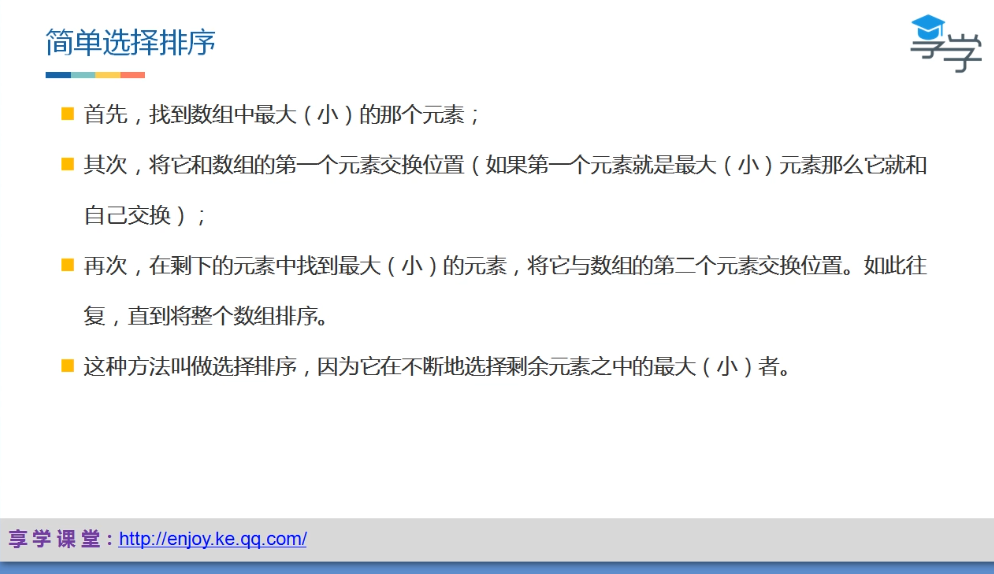
冒泡排序的优化
public class ChoiceSort{
public static int[] sort(int[] array){
if (array.length == 0)
return array;
for(int i=0;i<array.length;i++){
//存放最小数的下标
int minIndex = i;
for(int j=i;j<array.length;j++){
//找到最小的那个数
if(array[j]<array[minIndex]){
minIndex = j;
}
}
//交换
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
}
}
3.简单插入排序O(n2)

插入排序当前数据向后移动一位不会覆盖下一位的元素吗?
不会 比较一个移动一个,移动前后一个位置已经空出来了。
public class InstertionSort {
public static int[] sort(int[] array){
if (array.length == 0)
return array;
int currentValue;//待排序的数据
for(int i=0;i<array.length-1;i++){//默认第一个元素已经排序
int preIndex = i;//已排序数据的索引
currentValue = array[preIndex+1];
while(preIndex >= 0 && currentValue < array[preIndex]){
array[preIndex+1] = array[preIndex];
preIndex--;//遍历已排序的数组
}
array[preIndex+1] = currentValue;
}
}
}
4.分治法
1.希尔排序O(nlogn)

改进了简单插入排序,也称为缩小增量排序,突破了O(n2)
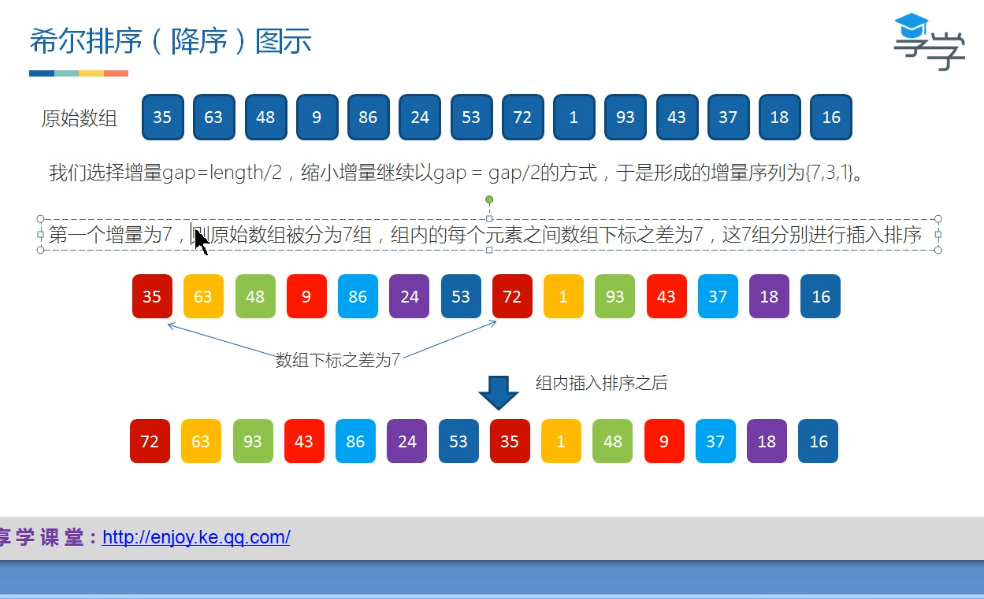
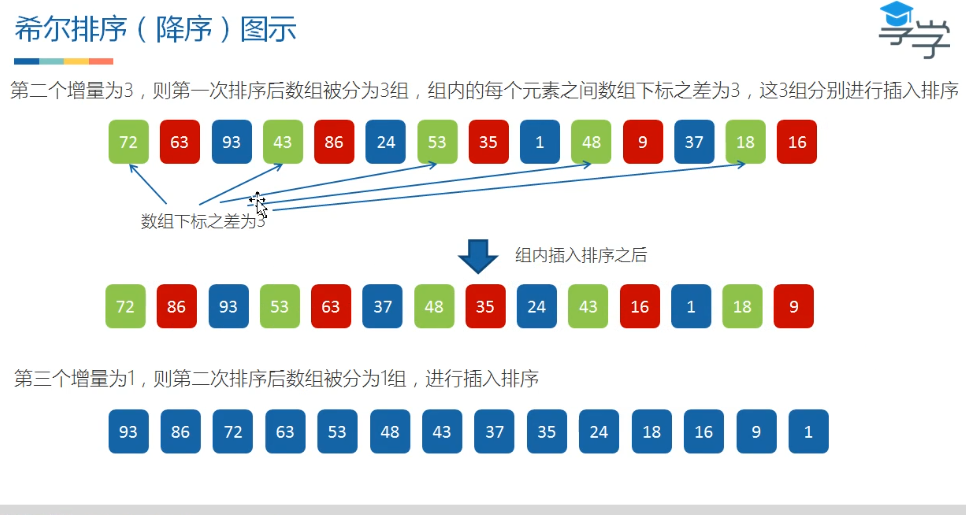
public class ShellSort{
public static int[] sort(int[] array){
if(array.length == 0)
return array;
}
int len = array.length;
int grap = len/2;
//组内待排序的数据
int currentValue;
while(grap>0){
for(int i=grap;i<len;i++)
currentValue = array[i];
int preIndex = i-grap;
while(preIndex>0&&array[preIndex]>currentValue){
array[preIndex + grap] = array[preindex];
preIndex = preIndex - grap;
}
}
grap = grap/2;
}

2.归并排序O(nlogn)
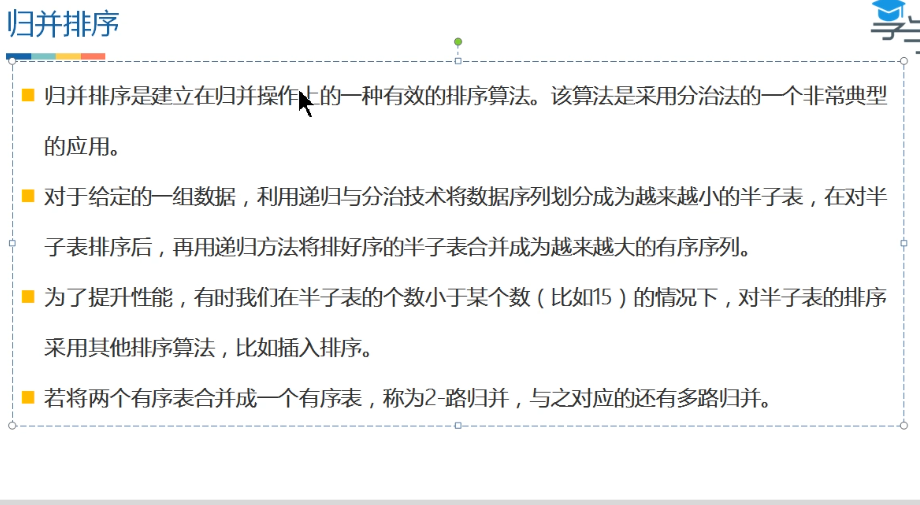

public class MergeSort{
public static int[] sort(int[] array){
//切分的位置
int mid = array.length/2;
int[] left = Arrays.copyOfRange(array,0,mid);
int[] right = Arrays.copyOfRange(array,mid,array.length)
return merge(sort(left),sort(right));
private static int[] merge(int[] left, int[] right){
int[] result = new int[left.length + right.length];
for(int index = 0.leftIndex = 0.rightIndex = 0;index<result.length;index++){
if(leftIndex>=left.length){
result[index] = right[rightIndex++]
}
else if(rightIndex>=right.length){
result[index] = left[rightIndex++]
}
else if(left[leftIndex]>=right.length){
result[index] = right[rightIndex++]
}
else{
result[index] = left[leftIndex++]
}
}
}
3.快速排序O(nlogn)
20世纪科学和工程十大算法
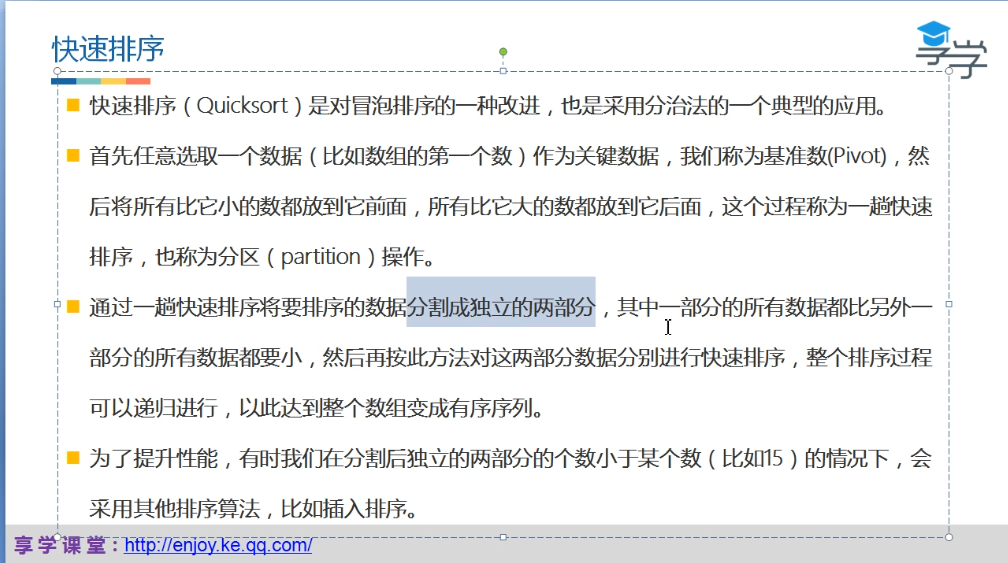


public class QuickSort {
public static int[] sort(int[] array, int start, int end){
if(array.length < 1 || start < 0 || end >= array.length || start > end)
return null;
//分区(割)指示器 = 一趟快速排序之后的返回值下标
int zoneIndex = partition(array,start,end);
//对左右两部分递归调用sort方法
if(zoneIndex > start){
sort(array,start,zoneIndex-1);
}
if(zoneIndex < end){
sort(array,zoneIndex+1,end);
}
return array;
}
private static in partition(int[] attay, int start,int end){
//基准数
int pivot = (int)(start+Math.random() * (end - start=1));
int zoneIndex = start - 1;
swap(array,pivot,end);//交换基准数和尾元素
for(int i= start;i<end;i+=){
if(array[i]<array[end]){
zoneIndex +=;
if(i>zoneIndex){
swap(array,i,zoneIndex);
}
}
}
return zoneIndex;
}
public static void swap(int[] array, int i, int j){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}

5.堆排序O(nlogn)
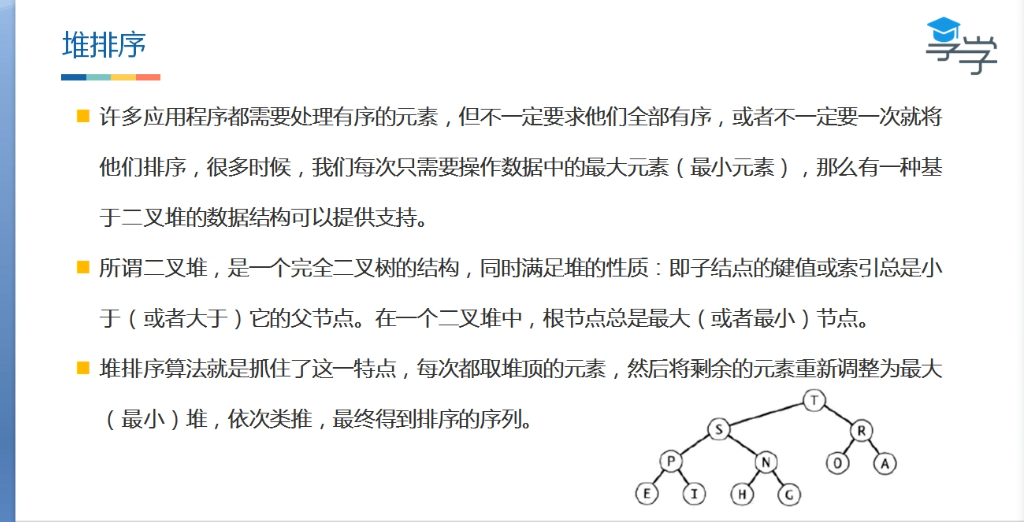
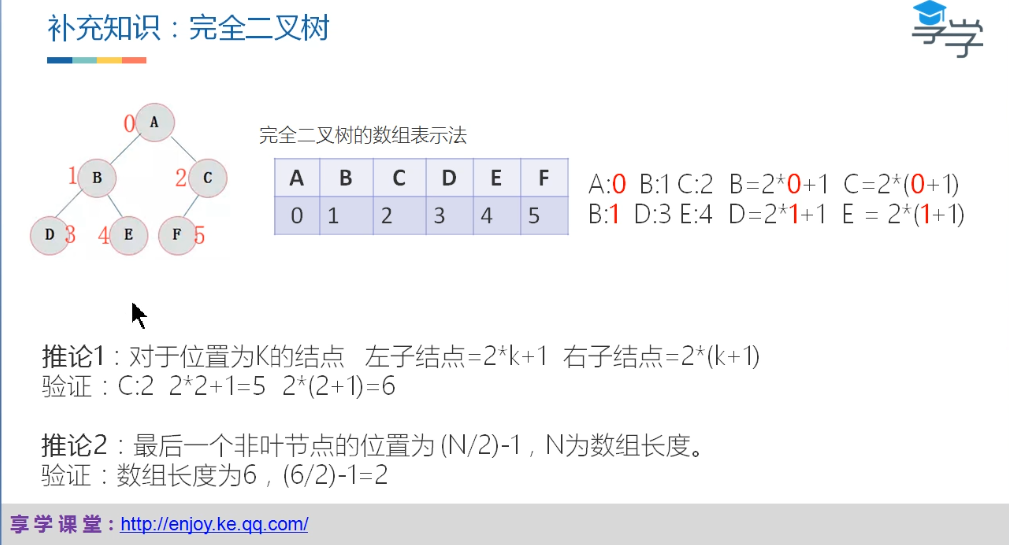

public class HeapSort {
//声明全局遍历。用于记录数组array的长度
private static int len;
private static int[] sort(int[] array){
len = array.length;
if(len<1) return array;
//构建一个最大堆
buildMaxHeap(array);
//取出堆顶元素和尾元素交换
while(len>0){
swap(array,0,len-1);
len--;//len -- 数组不变
adjustHeap(array,i);
}
return array;
}
}
//构建一个最大堆
private static void bulidMaxHeap(int[] array){
for(int i= (len/2-1);i>=0;i--){
adjustHeap(array,i);
}
}
//调整堆
private static void adjustHeap(int[] array,int i){
int maxIndex = i;//保存最大的元素
int left = 2*i+1;//左节点
int right = 2*(i+1);//右节点
if(left<len&& array[left]>array[MaxIndex]){
maxIndex = left;
}
if(right<len&& array[right]>array[MaxIndex]){
maxIndex = right;
}
if(maxIndex != i){
swap(array,maxIndex,i);
adjustHeap(array,maxIndex)
}
}
public static void swap(int[] array, int i, int j){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
6.桶
1.计数排序

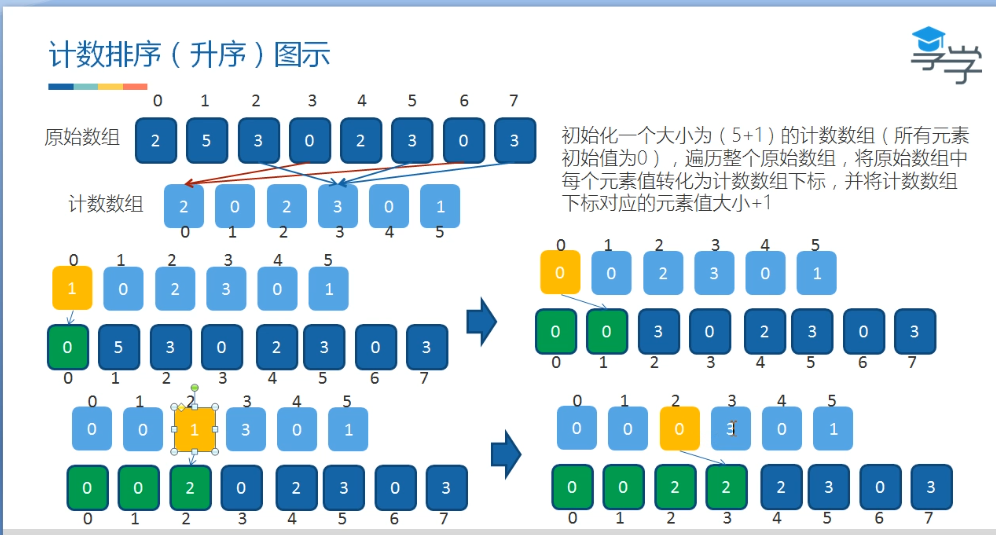
2.桶排序O(nlogn)


3.基数排序

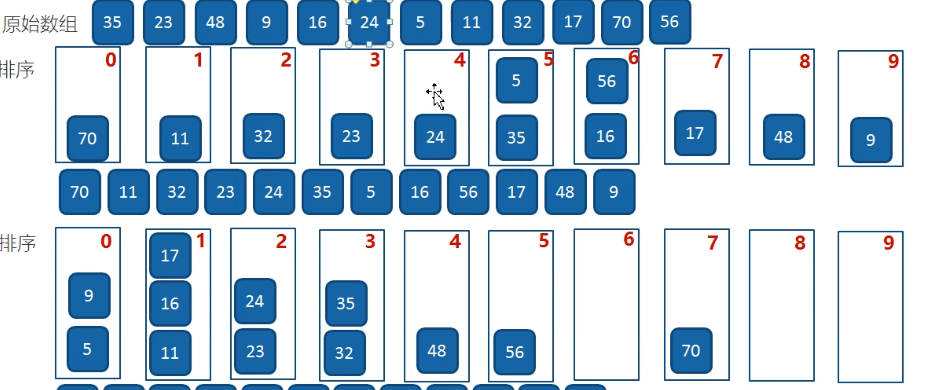
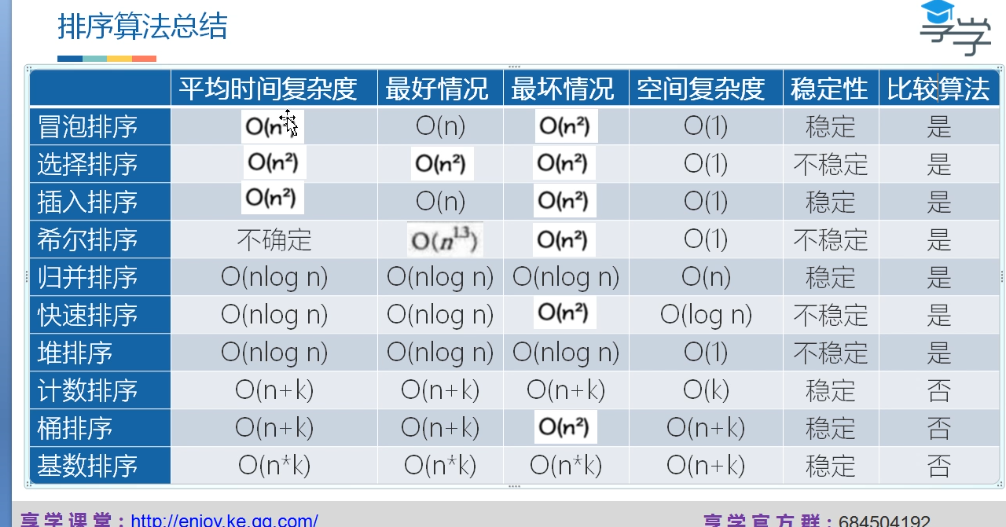
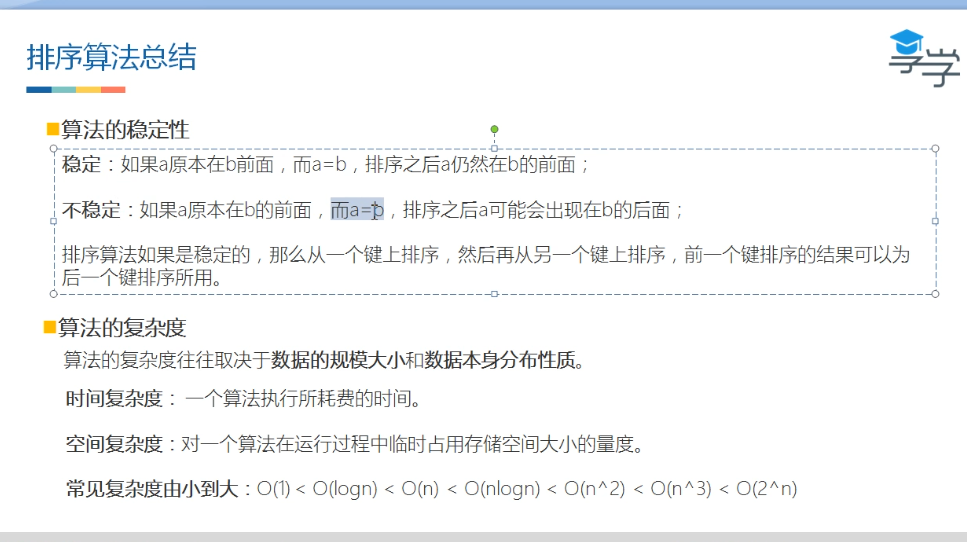
总结:


二分查找
前提:
数据已经有序排放在数组中,通过将待查的元素与数组最中间元素进行对比,如果大于中间值,则目标值可能存在于右半部分,否则可能在左半部分,查到为止
public class BinarySearch{
public static void main(String[] args){
int arr[] = {1,2,3,4,5,6,7,8,9,10};//源数据
int key = 8;
}
public static int biSerach(int arr[],int a){
int start = 0;
int end = arr.length - 1;
int mid;
while(start<=end){
mid = (start+end)/2;
if(arr[mid] < a){
end = mid+1;
}else if(arr[mid] > a){
end = mid - 1;
}else{
arr[mid];
}
}
return -1;
}
}