用来查找一个字符串中最长回文子串的方法
平时的暴力为 (n^3) ,而(Manacher)将时间复杂度提升到了线性,牛
(n^3) 实在太……,想到优化
枚举每一个字符,并以它为中心,向两边寻找回文串,当遍历完整个数组的后,就可以找到最长的回文串,时间复杂度 (O(n^2))
(Manacher) 只需 (O(n))
回文串的长度可奇可偶,aba(奇),abba(偶)
预处理(在每一个字符左右都加'#')那么无论奇偶,字符的个数都成了奇数,避免了分类讨论
$aba --> #a#b#a#$
$abba --> #a#b#b#a#$
类比 (KMP) 算法,我们处理一个P数组,(P[i])表示以(a[i])字符为中心的回文子串的半径(若(P[i] = 1),则该回文串就是 (a[i]) 本身)
关于半径
很明显我们求出最长的半径就知道最长回文串字符的个数,为啥??
举个栗子:
A:# 1 # 2 # 2 # 1 # 2 # 2 #
p:1 2 1 2 5 2 1 6 1 2 3 2 1
显然以中间'1'为中心的回文串半径最大为6;原串为22122,长度为5,正好为半径减一
奇数的举例也是如此,所以该办法可靠
关于起始位置
我们如果知道半径长度,但似乎无法定位子串,所以我们还要知道它的起始位置
solution:我们再在原串起始位置加一个$,所以起始位置就是中间位置减去半径再除以2
关于为什么加$,(避免与原串字符重复,进而不必改变P数组值)
举栗验证(实在不会啥证明方法,望大佬可以提供别的方法)
$#b#o#b# 中'o'的位置是 4 ,半径是 4,相减为 0,再除 2,依然是 0;
$#1#2#2#1#2#2# 中间'1'的位置为 8,半径是 6,相减为 2,再除 2 是 1 所以原串中最长子串'22122'起始位置为 1;
关于 (P) 数组的求法
有关变量:(mx):回文串能延伸到的最右端的位置;(id):为能延伸到最右端的位置的那个回文子串的中心点位置
核心代码:
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
====================================================================================
对称点:
(2 * id - i)是 (j) 关于中点 (id) 的对称点
(((i + j) / 2 = id) 方程两边同时乘以二, 得:(i + j = 2 * id) 移项, 得:(j = 2 * id - i))
=========================================================================================
1.当 (mx - i > P[j]) 的时候,以(A[j])为中心的回文串必然包含在以(A[id])为中心的回文子串中,所以必有P[i] = P[j], 见图
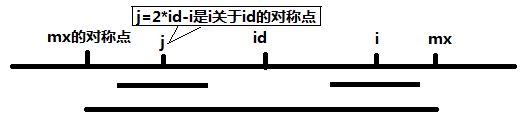
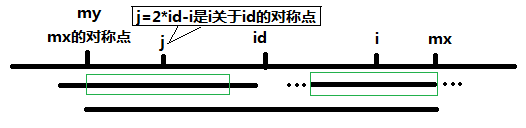
2.当 (A[j] >= mx - i) 的时候,以(A[j])为中心的回文子串不一定在
(A[id]) 为中心的回文子串中,但根据对称,下图中两个绿框所包围的部分是相同的,也就是说以 (A[i]) 为中心的回文子串,其向右至少会扩张到(mx)的位置,也就是说 (A[i] >= mx - i) 至于 (mx) 之后的部分是否对称,就只能老老实实去匹配了
3.对于 (mx <= i) 的情况,无法对 (A[i]) 做更多的假设,只能(A[i] = 1),然后再去匹配了
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int M = 51000100;
char a[M],s[M << 1];
int n,p[M << 1],ans = 1;
//===============================
void pre_(){
s[0] = s[1] = '#';
for(int i = 1;i <= n; i++){
s[i * 2] = a[i];
s[i * 2 + 1] = '#';
}
n = n * 2 + 1;
}
//===============================
void Mana_(){
int mx = 0,id;
for(int i = 1;i < n; i++){
if(i < mx)//在范围内manacher精髓
p[i] = min(p[(id << 1) - i],p[id] + id - i);//前两种情况
else
p[i] = 1;
while(s[i + p[i]] == s[i - p[i]])p[i]++;//继续扩展p[i]长度
if(i + p[i] > mx){
mx = i + p[i];//更新mx,id值
id = i;
}
}
}
int main(){
scanf("%s", a + 1);
n = strlen(a + 1);
pre_();
Mana_();
for(int i = 0;i <= n * 2 + 1; i++)
ans = max(ans, p[i]);
printf("%d", ans - 1);
}