[buaa-SE-2017]结对项目-数独程序扩展

结对项目-数独程序扩展

step1~step3:github:SE-Sudoku-Pair-master##

step4:github:SE-Sudoku-Pair-dev-combine##

step5:github:SE-Sudoku-Pair-dev-product##

Part1: PSP表-预估

PSP2.1	Personal Software Process Stages	预估耗时（分钟）
Planning	计划	120
Estimate	· 估计这个任务需要多少时间	5
Development	开发	10
Analysis	· 需求分析 (包括学习新技术)	300
Design Spec	· 生成设计文档	30
Design Review	· 设计复审 (和同事审核设计文档)	5
Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10
Design	· 具体设计	30
Coding	· 具体编码	1440
Code Review	· 代码复审	60
Test	· 测试（自我测试，修改代码，提交修改）	180
Reporting	报告	10
Test Report	· 测试报告	10
Size Measurement	· 计算工作量	10
Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60
Total	合计	2280

Part2: Information Hiding, Interface Design, Loose Coupling

2.1 Information Hiding

Information hiding is part of the foundation of both structured design and object-oriented design. In structured design, the notion of “black boxes” comes from
information hiding. In object-oriented design, it gives rise to the concepts of encapsulation and modularity, and it is associated with the concept of abstraction.
引自代码大全，见：http://www.cnblogs.com/magiccode1023/archive/2012/10/23/2736257.html

不用多说，最基本的抽象原则，保证程序的健壮性和灵活性。
上述链接中也提到了，信息隐藏要隐藏的信息包括两方面：

1.隐藏可能的复杂性。
2.隐藏外部改变会有危险的信息。

隐藏复杂性中隐藏了分而治之的思想，而第2点则是为了程序的安全性。
代码中的很多地方都隐藏了复杂性：

for (int k = 1; k <= LEN; ++k) {
		if (Sudoku::count >= number) return;
		if (checkGeneratePos(i, j, k)) {   //check if it is ok to set k on (i,j)
			board[i][j] = k + '0';
            traceBackWriteFile(i, j + 1, number, outFile);    //if can,recur to next place
		}
	}

上述代码是回溯函数中的一部分，checkGeneratePos(i,j,k)就是一个典型的复杂性隐藏，它隐去了方法实现的内部细节，从而让我们能专注于实现主要的算法。

我们在coding中避免类成员和一些辅助函数暴露，所以将它们设置为private：

private:
	char board[LEN + 1][LEN + 1];
	void init();
	inline void traceBackN(int i, int j, int n, int result[][LEN*LEN]);
	inline bool traceBackSolve(int i, int j);
	inline int getBlock(int i);
	void traceBackWriteFile(int i, int j, int number, fstream &outFile);
	void traceBackCountSolution(int i, int j, int *solutionNumber, int bound);
	void digHoles(int count, int mode, int lower, int upper, int result[][LEN*LEN]);
	static long int count;

上述方法或者类成员一旦在外部被调用就会以不正常的方式修改类，所以需要避免。
我们设计方法的一个很重要的原则就是：这个方法具有单一的功能。有些时候总有一些控制方法会整合很多功能，这个时候我们需要分解这些功能为一个个小的功能，并分别实现它们。

2.2 Interface Design

Interface Design简单来说就是事先约定好模块的接口，这次实现的两个generate接口以及solve接口都是这个的体现，因为对接口有严格的规定，在step4我们互换Core模块的时候才没有太多的麻烦，很容易就完成了代码。

2.3 Loose Coupling

松耦合在下面链接中有较好的解释:
stackoverflow-Loose Coupling
其中心思想就是尽量减少模块之间的“依赖”，最理想的状态大概是更换程序中任何一个方法或是函数都只需要在方法或函数内部进行更改，这也是抽象的一种体现，个人认为实现这个原则的最好方法就是在各个模块之间的输入输出之间增加抽象层，这就相当于“松弛”了各个模块之间的耦合。

我们实现的solve方法很好地说明了这一点：

bool Sudoku::solve(int puzzle[], int solution[]) throw(IllegalLengthException) {
	bool ret;
	convertToTwoDimension(puzzle);
	ret = traceBackSolve(1, 1);
    if (!check()) {
        return false;
    }
	convertToOneDimension(solution);
	return ret;
}

这个方法中convertToOneDimension会把当前数独的解复制到solution中，我们并不是直接将类成员中的数组传出，我们实际上就是在方法的输出上增加了抽象层。这样的方法使得如果当我们将数独类成员中的数组换成1维数组（原来是2维）的时候，我们只需要在convertToOneDimension内部进行修改。

Part3: 计算模块的设计和实现

我们主要的算法逻辑都集中在Sudoku这个类当中。

• 数独求解的部分我们使用回溯的思想进行解决。回溯方法traceBackSolve()对第i行第j列元素及其后方（先向右，到最右则折返换行）空格进行求解，每次求解尝试从1到9，检测1到9每个数字是否适合在此格子中填入（行、列、宫不重复），并在尝试中递归调用traceBackSolve()方法，从而验证每次尝试的正确性。求解数独的接口solve()方法负责调用traceBackSolve()方法进行求解，并做一二维数组的转换。

• 在生成数独接口generate(int number, int lower, int upper, bool unique, int result[][])中，我们采用先生成终盘，再从终盘中挖空的形式进行数独生成。首先调用generateCompleteN()这个已经实现的生成终盘方法，得到number个终盘，再使用digHoles()方法进行挖空。挖空策略一共有两种，一种为从头数独第一个数开始，一种为随机选择。随机挖空由于速度较快，但容易出现挖出来的盘有多解的情况，我们只在unique为假的情况下使用它。unique为真时，采用顺序挖空的策略，以从左到右，从上到下的顺序进行挖空，每次挖空之后，将原始数字用1到9中其他数字进行替换，并调用solve()对数独进行求解，若能解出，则证明此空不能挖，否则可挖，继续向后挖空。

• 第二个生成数独接口二generate(int number, int mode, int result[][LEN*LEN])中，我们利用了第一个generate()方法，根据mode得到相应的up和down传入generate()，便可得到结果。

Part4: UML图

UML图如下：

相互之间没有依存关系。

Part5: 计算模块的性能改进

5.1 -c

下图展示了生成1000000个完整数独的性能分析

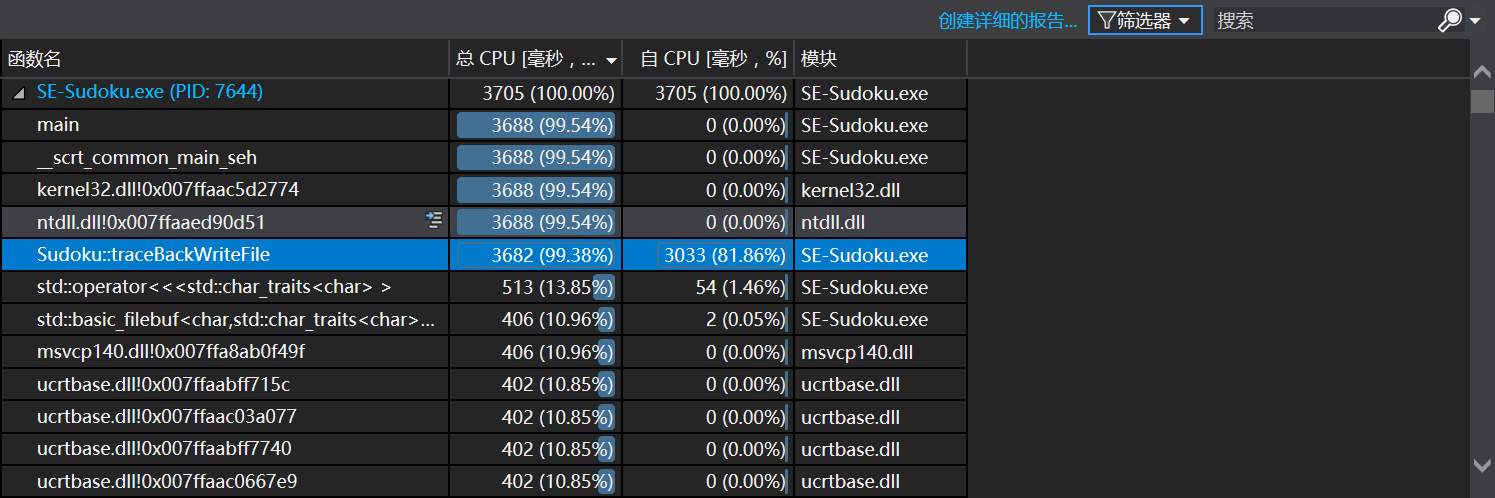
由于这次继承了我上次的代码，所以代码本身已经被优化过。
5.272秒，几乎所有的时间都花费在回溯递归上，速度已经可以接受。
一个可能的优化是在判断重复的时候使用位操作。

5.2 -s

下图展示了解1000个数独时候的性能分析：

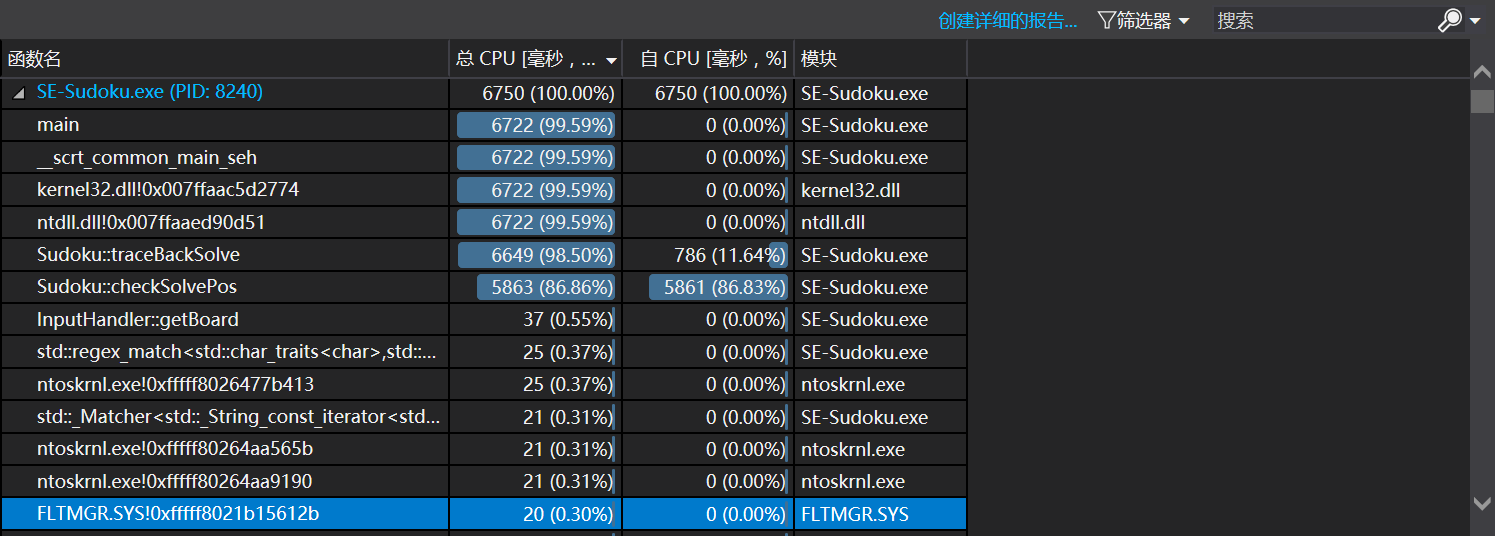
首先注意到checksolve花费较长时间，这个函数原来使用了3×9的时间来判断，注意到这个方法的下界是1×9，遂更改了实现方式：

    int row, col;
    row = getBlock(i);
    col = getBlock(j);
    for (int a = 1; a <= LEN; ++a) {
        if ((board[i][a] == k + '0') || (board[a][j] == k + '0') 
                || (board[row + ((a - 1) / 3)][col + ((a - 1) % 3)] == k + '0'))
            return false;
    }	

不过，这是常数级别的优化，所以效果很差，改进之后再次性能分析发现效果微弱。
一个可能的改进是使用bitmap来优化。

5.3 -n

直接在-u模式下测试，由于当r的参数的值变大的时候生成10000个解的时间几乎不可接受，所以选择较低的数值，下图是指令-n 10000 -r 25~55的效能分析：

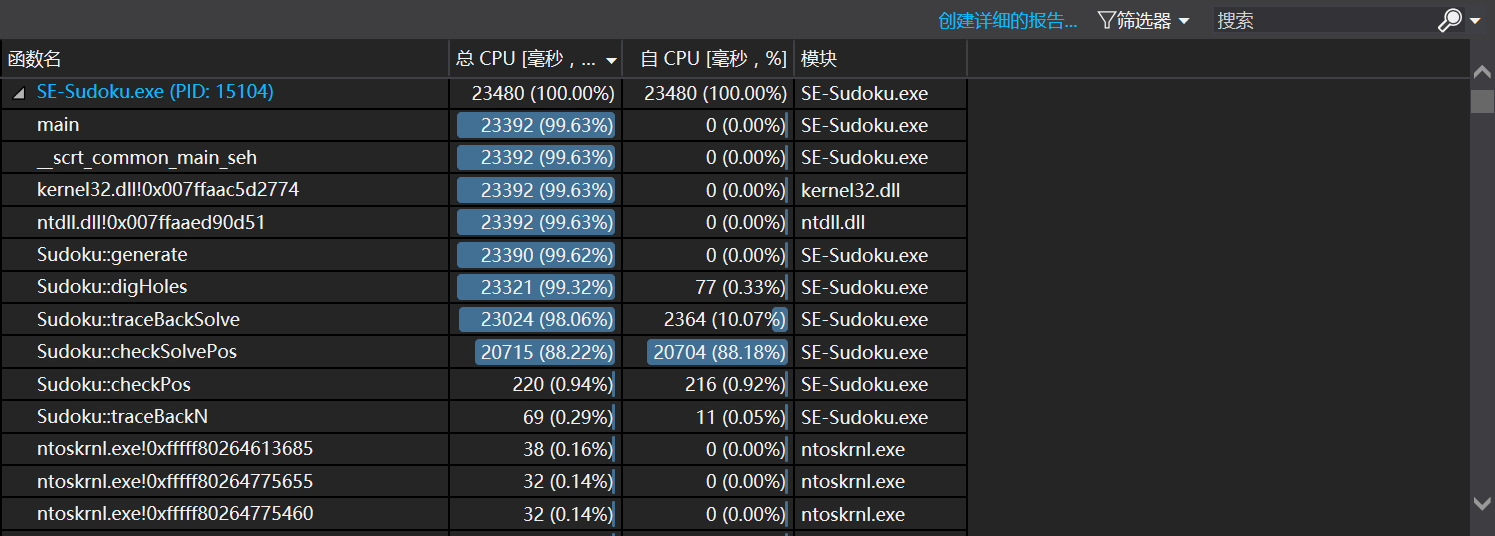
24秒
热路径主要集中于solve函数，判断原因还是由于递归时造成的指数级增长的函数调用，在不更改现有结构的情况下已经很难改进。

改进效能花费了30分钟。

Part6: Design by Contract & Code Contract

契约式编程我们已经在OO课上实践过，其中心思想为：在完成代码模块的时候，首先制定“契约”，它描述这个模块的一些性质，包括调用时候满足的前置条件(precondition)、方法完成时候满足的后置条件(postcondition)、方法抛出的异常(exception)以及方法满足的不变式(invariant)，最后根据“契约”来完成代码。一个比较典型的契约式编程的例子就是Assert语句了。
这种编程方式首先假定所有输入都满足前置条件（precondition），而与其相反的防御式编程则假定输入会有所有可能的情况，包括正确和错误的。
很明显，契约式编程非常适合于在程序开发时使用，同时也有很多工具简化了这种编程方式，这次给出的参考链接中，Code Contracts for .NET就是一个这样的工具，这个工具可以自动检测模块中的契约来测试它们是否满足条件，从而实现Runtime checking,static checking等功能。不过，在程序发布的时候一般需要取消契约检查，因为它对性能也有一定影响。

契约式编程非常有助于错误的精确定位，虽然绝大多数流行的程序语言在程序运行出错时都会在一定程度上给出提示，但我们更希望在早期发现程序的错误，而不是等到错误一层层传递到顶层才发现他们。

总结来说，契约式编程在设计层面保证了程序的正确性，但当我们将程序发布，我们就必须做好准备应付各种可能的错误，而不是等待用户去满足契约了。

这次实现的Core计算模块的接口也是一种契约，比如generate(int number,int lower,int upper,bool unique,int result[][])方法中，调用者需要满足参数的一些条件，而这个方法也需要满足在方法完成之后在result数组中存储number个规定的数独游戏的后置条件(postcondition)，我们在测试的时候，也是根据这些条件进行测试的。

Part7: 计算模块单元测试

7.1 solve函数

测试思路：给出一个题目，和答案对比。

ret = sudoku.solve(puzzle, temp);
Assert::AreEqual(ret, true);
for (int i = 0; i < 81; ++i) {
	Assert::AreEqual(temp[i], solution[i]);
}

7.2 generate函数

测试思路：对-r指令，首先在生成之后用solve函数测试是否可解，然后计算游戏中的空的个数，判断是否满足要求；对-u指令，在-r的基础之上用回溯法求出解的个数，如果个数大于1，则出错，测试-m的时候也是类似的方式。
下面是测试-n 10 -r lower~upper -u 的部分代码：

			sudoku.generate(10, lower, upper, true, result);
			for (int i = 0; i < number; ++i) {
				Assert::AreEqual(sudoku.solve(result[i], solution), true);
				int solutionNumber = sudoku.countSolutionNumber(result[i], 2);
				Assert::AreEqual(solutionNumber, 1);
				int count = 0;
				for (int j = 0; j < 81; ++j) {
					if (result[i][j] == 0) count++;
				}
				Assert::AreEqual(count <= upper && count >= lower, true);
			}

7.3 测试异常

测试思路：设置一个bool型变量exceptionThrown（初始值为false）以及异常的条件，只要catch到异常，就将exceptionThrown设置为true，然后进行断言。
下面是测试SudokuCountException的代码：

			bool exceptionThrown = false;
			try { // Test first SudokuCountException
				sudoku.generate(-1, 1, result);
			}
			catch (SudokuCountException& e) {
				exceptionThrown = true;
				e.what();
			}
			Assert::IsTrue(exceptionThrown);

这里generate方法生成的数独个数不能是负数，所以会抛出异常。

7.4 测试输入参数的分析

测试思路：用strcpy_s初始化argv，设置argc，然后进行调用相关方法进行分析和断言。
下面是测试指令-n 1000 -m 2的代码：

			InputHandler* input;
			strcpy_s(argv[3], length, "-n");
			strcpy_s(argv[4], length, "1000");
			strcpy_s(argv[1], length, "-m");
			strcpy_s(argv[2], length, "2");
			argc = 5;
			input = new InputHandler(argc, argv);
			input->analyze();
			Assert::AreEqual(input->getMode(), 'n');
			Assert::AreEqual(input->getNumber(), 1000);
			Assert::AreEqual(input->getHardness(), 2);
			delete input;

这里打乱了参数的顺序，其他参数的组合也是用类似的方法来测试的。

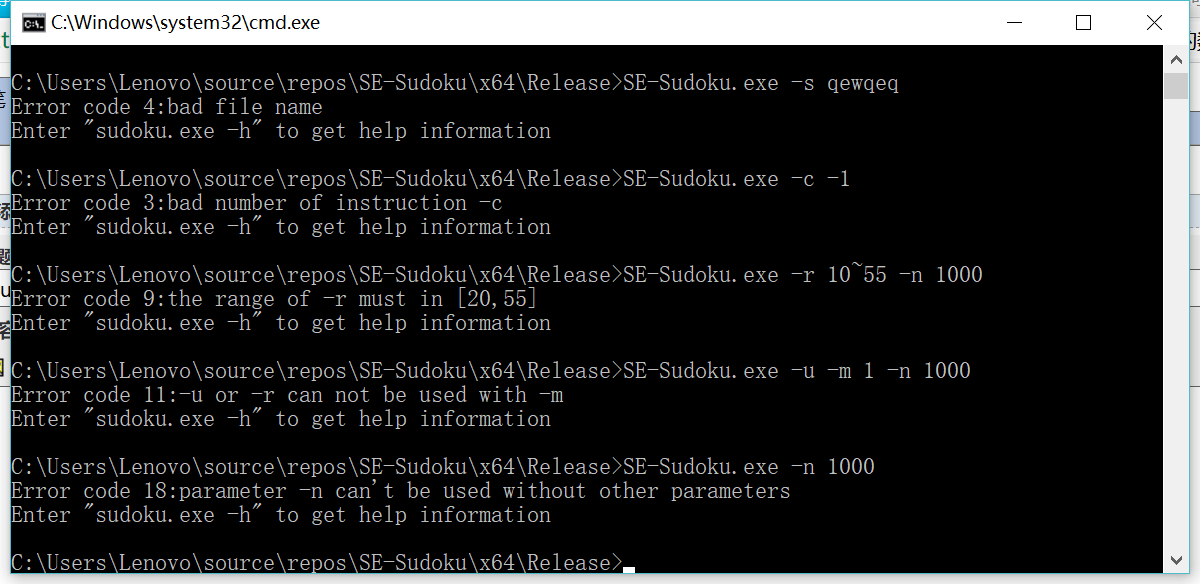
7.5 参数解析鲁棒性测试

我们的program中，参数错误的情况下会直接报错然后退出，同时输入分析在完成之后一般不会改变，所以我们直接在控制台中进行了测试，主要看是否有相应的输出，错误种类参看下图：

Error Code	异常说明	错误提示
1	参数数量不正确	bad number of parameters.
2	参数模式错误	bad instruction.expect -c or -s or -n
3	-c指令的数字范围错误	bad number of instruction -c
4	-s指令找不到文件	bad file name
5	-s指令的puzzle.txt中的数独格式错误	bad file format
6	-s指令的puzzle.txt中的数独不可解	bad file can not solve the sudoku
9	-r指令后的数字范围有错误	the range of -r must in [20,55]
10	-m指令后的模式有错误	the range of -m must be 1,2 or 3
11	11 -m指令与-u或-r指令同时出现	-u or -r can not be used with -m
12	c指令的参数范围错误	the number of -c must in [1,1000000]
13	-n指令的参数范围错误	the number of -n must in [1,10000]
14	-n指令的参数类型错误	the parameter of -n must be a integer
18	-n不能单独使用	parameter -n cann't be used without other parameters

其中code不连续是因为有的code替换成了exception。

一些测试情景可以参考下图：

7.6 单元测试覆盖率分析

总的覆盖率约为94%
没有测到的代码主要是Output相关的代码，已经在7.5节进行了说明。

Part8: 计算模块异常处理

下图展示了我们对于异常的设计：

Error Code	异常类	异常说明	错误提示
8	SudokuCountRangeException	generate(int number,int lower,int upper,bool unique,int result[][])中number范围错误	number in generate(int number,int lower,int upper,bool unique,int result[][]) must in[1,10000]
16	LowerUpperException	generate(int number,int lower,int upper,bool unique,int result[][])中lower和upper的值错误	the lower and upper in generate(int number,int lower,int upper,bool unique,int result[][]) must satisfy:lower<upper,lower > 20,upper < 55
17	ModeRangeException	generate(int number, int mode, int result[][])函数中mode的值错误	the number of mode must in [1,3]

下面分别给出异常对应的测试样例，测试方法已经在之前说明。

8.1 SudokuCountException

			int result[1][81];
			bool exceptionThrown = false;
			try { // Test first SudokuCountException
				sudoku.generate(0, 1, result);
			}
			catch (SudokuCountException& e) {
				exceptionThrown = true;
				e.what();
			}
			Assert::IsTrue(exceptionThrown);

                        exceptionThrown = false;
			try {
				sudoku.generate(100000, 20, 50, true, result);
			}
			catch (SudokuCountException& e) {
				exceptionThrown = true;
				e.what();
			}
			Assert::IsTrue(exceptionThrown);

上例中两次调用generate函数，生成数量分别为0和100000，都会抛出异常。

8.2 LowerUpperException

			//test LowerUpperException,case 1
			exceptionThrown = false;
			try {
				sudoku.generate(1, 1, 50, true, result);
			}
			catch (LowerUpperException& e) {
				exceptionThrown = true;
				e.what();
			}
			Assert::IsTrue(exceptionThrown);
			//test LowerUpperException,case 2
			exceptionThrown = false;
			try {
				sudoku.generate(1, 20, 56, true, result);
			}
			catch (LowerUpperException& e) {
				exceptionThrown = true;
				e.what();
			}
			Assert::IsTrue(exceptionThrown);
			//test LowerUpperException,case 3
			exceptionThrown = false;
			try {
				sudoku.generate(1, 50, 1, true, result);
			}
			catch (LowerUpperException& e) {
				exceptionThrown = true;
				e.what();
			}
			Assert::IsTrue(exceptionThrown);

上例中测试了upper和lower抛出异常的3种情况，分别是lower超出范围，upper超出范围和lower、upper不满足lower<upper的情况

8.3 ModeRangeException

			//test ModeRangeException
			exceptionThrown = false;
			try {
				sudoku.generate(1, -1, result);
			}
			catch (ModeRangeException& e) {
				exceptionThrown = true;
				e.what();
			}
			Assert::IsTrue(exceptionThrown);

上例中generate调用的模式出错，只能是1、2、3，所以抛出异常。

Part9: 界面模块设计

9.1 风格

• 界面风格采用QSS文件统一修改。QSS代码改自csdn博客作者一去、二三里的黑色炫酷风格。
  基本风格见下图

• Hint按钮风格：

QPushButton#blueButton {
        color: white;
}
QPushButton#blueButton:enabled {
        background: rgb(0, 165, 235);
        color: white;
}
QPushButton#blueButton:!enabled {
        background: gray;
        color: rgb(200, 200, 200);
}
QPushButton#blueButton:enabled:hover {
        background: rgb(0, 180, 255);
}
QPushButton#blueButton:enabled:pressed {
        background: rgb(0, 140, 215);
}

• 数独棋盘单元格风格（普通格、角落格、宫边缘格）：

QPushButton#puzzleButton {
	border- 1px;
	border-style: solid;
	border-radius: 0;
}
QPushButton#puzzleButtonTLCorner {
    	border-radius: 0;
	border-top-left-radius: 4px;
	border- 1px;
    	border-style: solid;
}
QPushButton#puzzleButtonTRCorner {
	border-radius: 0;
	border-top-right-radius: 4px;
    	border- 1px;
    	border-style: solid;
}
QPushButton#puzzleButtonBLCorner {
	border-radius: 0;
	border-bottom-left-radius: 4px;
    	border- 1px;
    	border-style: solid;
}
QPushButton#puzzleButtonBRCorner {
	border-radius: 0;
	border-bottom-right-radius: 4px;
    	border- 1px;
    	border-style: solid;
}
QPushButton#puzzleButtonRE {
	border-radius: 0;
	border- 1px;
	border-right- 3px;
    	border-style: solid;
}
QPushButton#puzzleButtonBE {
	border-radius: 0;
    	border- 1px;
	border-bottom- 3px;
    	border-style: solid;
}
QPushButton#puzzleButtonBRE {
	border-radius: 0;
    	border- 1px;
        border-right-3px;
	border-bottom- 3px;
	border-style: solid;
}

小结：界面风格不是我们在设计UI时最早考虑的部分，本来打算风格只进行简单修改，只用setStyleSheet()方法来设计界面风格。不过后来发现自带的界面实在太丑，于是决定借鉴已有的风格，针对项目要求进行调整，最终效果还算不错。

9.2 布局

• 布局设计采用纯代码的设计，使用Layout进行对齐。

• 欢迎、帮助与选择难度界面统一使用QVBoxLayout对控件进行对齐
  效果见下图
  
  
  

• 游戏界面采用Layout嵌套Layout的形式进行布局管理。我们先设计了一个mainLayout作为最外层Layout,将其他Layout竖直放入mainLayout。
  其他Layout见下图
  

• 为保持数独棋盘排列的紧密，在棋盘周围加了spacer把棋盘上的格子挤压到一起，且能保持形状。

• 为保证比例的美观，游戏窗体被强制固定，无法进行缩小与放大。

小结： 设计布局过程有些小曲折，一开始由于没有经验，不知道该如何用代码该出想要的布局效果，也想过不使用代码修改布局，直接在界面上拖拽。但考虑到代码的灵活性，还是决定使用代码，放弃了拖拽设计（下次有机会做UI，希望尝试下拖拽设计和代码设计结合的形式）。好在有博客和Qt官方文档的支持，还是成功学会了Qt的布局设计，做出了当前这个效果。

Part10: 界面和计算模块对接

10.1 generate

主要在开始新游戏的时候使用，首先用generate中生成数独游戏，然后再转换成QString显示在界面的button上，部分代码如下：

	int result[10][LEN*LEN];
	sudoku->generate(10, degOfDifficulty, result);
	QString temp;
	QString vac("");
	for (int i = 0; i < LEN; ++i) {
		for (int j = 0; j < LEN; ++j) {
			if (result[target][i*LEN + j] == 0) {
				tableClickable[i][j] = true;
				puzzleButtons[i][j]->setText(vac);
				puzzleButtons[i][j]->setEnabled(true);
				puzzleButtons[i][j]->setCheckable(true); // Able to be checked
			}
			else {
				tableClickable[i][j] = false;
				puzzleButtons[i][j]->setText(temp.setNum(result[target][i*LEN + j]));
				puzzleButtons[i][j]->setEnabled(false); // Unable to be editted
			}
		}
	}

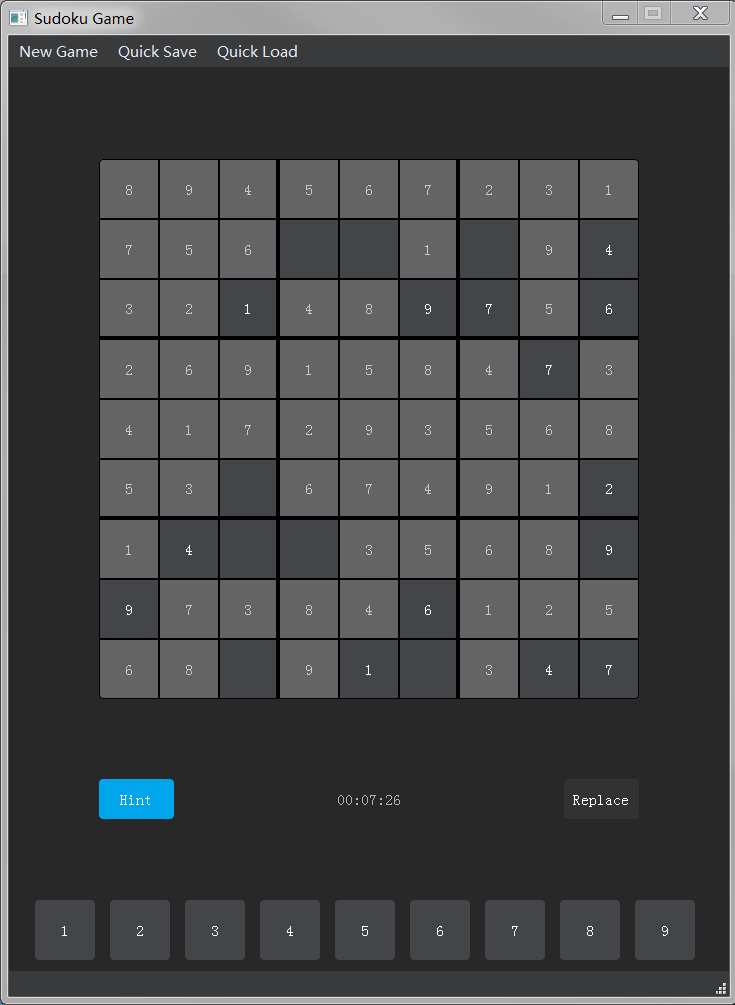
对于已经有数字的位置，则设置按钮不可用，一个样例的盘面如下：

10.2 solve

主要用在提示功能上，首先判断是否可解，如果可解则在相应的位置上给出提示，不可解则给出相应的提示，部分代码如下：

 if (sudoku->solve(board, solution)) {
        puzzleButtons[currentX][currentY]->setText(QString::number(solution[currentX*LEN + currentY]));
        puzzleButtons[currentX][currentY]->setChecked(false); // Set button unchecked
        checkGame();
    } else {
        QMessageBox::information(this, tr("Bad Sudoku"), tr("Can not give a hint.The current Sudoku
 is not valid
Please check the row,rolumn or 3x3 block to correct it."));
    }

Part11: 结对过程

这次我们的结对过程比较顺利，双方都能做到互相理解支持，我们的大部分工作在国庆期间完成，过程按照《构建之法》上讲到的，1小时切换一次。我的partner有些缺乏积极性，所以虽然有点不好意思不过我会去督促他，这样就保证了效率，另一方面我在UI设计上经验不足，我的partner解决了这个问题。我认为我们基本实现了取长补短。
同时我也体会到了在高强度编程的时候，高频次地更换驾驶员和领航员的职责是很有必要的，这样会缓解疲劳和压力，从而提高了代码的质量。
不过，在结对的过程中，我也因为编程过程被人监督而有些不自在，感觉没有完全发挥自己的水平。
总体而言，我认为我们发挥了结对编程的优势，但要进一步提高效率和质量，也许我和partner之间需要更多的磨合。

下面是队友的感受：

我们结对的过程总体来说算是不错的，成功完成了基本功能要求与附加的Step4、Step5。我们的大部分工作在国庆期间完成，那段时间严格遵守结对编程规范，一人敲代
码，另一人在一旁帮助审核代码与提供思路，每一小时进行工作交换，每次交换都把代码push到Github上，记录这一步工作的结果。我们用了三天时间实现了逻辑部分的> 完善与测试，并搭建起了UI的三个页面框架，总体效率还算不错。期间也遇到过找不着源头的bug，费了我们不少时间，不过好在是两个人合力查资料、想办法，最终还是> 解决了问题。国庆过后由于两人的时间不太能凑得上，我们便将工作分工，一人主攻功能，一人主攻界面，一步步推进项目并达到预期目标。

以下为我们二人结对编程时的照片。

Part12: 结对编程

12.1 结对编程的优缺点

• 优点

  • 两人可以随时交流，领航员会不断复审代码，因此代码的质量得到有效地提高
  • 两人合作效率高、体量小，这样灵活和高效兼具，非常适合小项目地开发。
  • 由于自己的代码不断被审阅，所以驾驶员会专注在代码上，比平时更加认真。
  • 两人互换角色很适合在高强度编程时保持代码的质量。

• 缺点

  • 编程变成了一种“表演”，一些人可能受不了这种丧失个人技术习惯被暴露的感觉。
  • 如果两人的了解和合作不够深入，那么代码会受到双方风格不一致的影响，反而有可能降低程序质量，所以事先讲好一些规则是很重要的。
  • 当两人的时间表不一致的时候，合作几乎变得不可能。
  • 领航员很多时候要指出代码中的问题，这就意味着从某种程度上指责partner，但是很多人可能并不愿意这样做。

在我看来，如果想要发挥结对编程的全部作用，就需要本人和partner之间加深了解和合作、互相不介意暴露问题、并且深刻领会领航员和驾驶员的职责所在，取长补短，这样才能有好的结果。

12.2 结对每个人的优缺点

我们互评了优缺点，结果如下:

• 15061119
  优点：
  1.极高的编码效率。
  2.专注于解决每个问题。
  3.充满责任心与工作热情。
  缺点：
  1.编码风格不太统一。

• 15061104
  优点：
  1.能理解支持partner。
  2.能力较强。
  3.解决了我一直苦恼的设计问题。
  缺点：
  1.某种程度上，欠缺一些积极性。

以下是我的自我评价：

• 自我评价：
  缺点：
  1.对partner的理解还不够
  2.有一点独断专行
  3.有些事情喜欢藏着，不愿意交流。

Part13: Step4实现

在博客中指明合作小组两位同学的学号，分析两组不同的模块合并之后出现的问题，为何会出现这样的问题，
以及是如何根据反馈改进自己模块的。

13.1 合作小组学号

15061111
15061129

13.2 合并之后出现的问题

13.2.1 问题1：dll生成的环境不同

• 问题描述
  我们组的dll在64位下生成，而合作小组的是在32位下生成的，这样导致模块不可调用。

• 解决方案
  重新生成了64位的dll，问题解决。

13.2.2 问题2：接口名不同

• 问题描述
  我们合作小组的接口为：

SODUCORE_API void generate_m(int number, int mode, int **result);
SODUCORE_API void generate_r(int number, int lower, int upper, bool unique, int **result);
SODUCORE_API bool solve_s(int *puzzle, int *solution);

而我们自己的接口为：

void generate(int number, int lower, int upper, bool unique, int result[][LEN*LEN]);
void generate(int number, int mode, int result[][LEN*LEN]);
bool solve(int puzzle[], int solution[]);

这就导致改变计算模块之后需要改名字。

• 解决方案
  把相应接口的名称更换即可

13.2.3 问题3：参数规格不同

• 问题描述
  注意到在13.2.2的双方的接口中，我们组定义result位二维数组，而合作小组定义为二维指针，这就导致参数错误。

• 解决方案
  将result转换位二维指针即可。

Part14: Step5实现

我们在step4的基础上进行了增量开发，主要实现了:帮助、错误提示、快速存档读档以及继续游戏的功能。

14.1 帮助

我们在主界面加入了帮助按钮，进入之后会显示数独的规则以及一个完整的数独：

用户点击return按钮可以返回到主界面。

14.2 错误提示

错误提示就是当用户填入的数字不满足数独的约束条件的时候，对不满足的数字对标红，这样用户可以很容易发现自己的错误，参看下图：

上图中填入的1和同列以及同行的1冲突，所以显示为红色，更改之后颜色回复正常：

14.3 快速存档/读档

用户进入游戏之后如果想要保存当前的盘面，则只需要点击菜单栏的QuickSave进行存档，之后如果想回到存档时候的状态，则只需要点击QuicjLoad。

点击QuickSave存档：

继续游戏：

然后点击QuicjLoad相应的存档点：

恢复：

14.4 继续游戏

当用户上次未完成游戏直接退出，再一次进入游戏可以点击Continue来恢复界面：

点击之后恢复：

14.5 功能反馈

Part15: PSP表-实际

PSP2.1	Personal Software Process Stages	实际耗时（分钟）
Planning	计划	180
Estimate	· 估计这个任务需要多少时间	5
Development	开发	10
Analysis	· 需求分析 (包括学习新技术)	300
Design Spec	· 生成设计文档	20
Design Review	· 设计复审 (和同事审核设计文档)	5
Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10
Design	· 具体设计	50
Coding	· 具体编码	2700
Code Review	· 代码复审	180
Test	· 测试（自我测试，修改代码，提交修改）	240
Reporting	报告	10
Test Report	· 测试报告	10
Size Measurement	· 计算工作量	10
Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60
Total	合计	3790

Part16: 总结

这次作业中，我收获了很多，我学会了如何用Qt进行GUI设计、以及如何将程序导出成DLL进行复用，同时我也实践了结对编程。
通过这次的结对编程我对合作的优势和劣势有了更深的体会，如果两人的之间有足够的支持，并能积极改进自身的缺点，就能很好地进行合作，合作的重点就在于对事不对人、取长补短和理解包容。