说的非常清楚,转之
from--https://zhuanlan.zhihu.com/p/67092151
模型概述
模型目标是:进行词的向量化表示(类似于Word2vec),使得向量之间尽可能的蕴含语义和语法的信息。
输入:语料库
输出:词向量
流程主要分为如下两个步骤:首先统计共现矩阵;训练词向量
统计共现矩阵
设共现矩阵为 ![[公式]](https://www.zhihu.com/equation?tex=X) ,其元素为
,其元素为 ![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%2Cj%7D) 。
。
![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%2Cj%7D) 的意义为: 在整个语料库中,单词
的意义为: 在整个语料库中,单词 ![[公式]](https://www.zhihu.com/equation?tex=i) 和单词
和单词 ![[公式]](https://www.zhihu.com/equation?tex=j) 共同出现在一个窗口中的次数。
共同出现在一个窗口中的次数。
例如下面的例子——
有三句话的语料:
- I like deep learning.
- I like NLP.
- I enjoy flying.
假设我们把统计窗口设定为1(即前后各1个词为上下文的词),那么统计中心词和上下文词共同出现的频次矩阵,即共现矩阵如下:
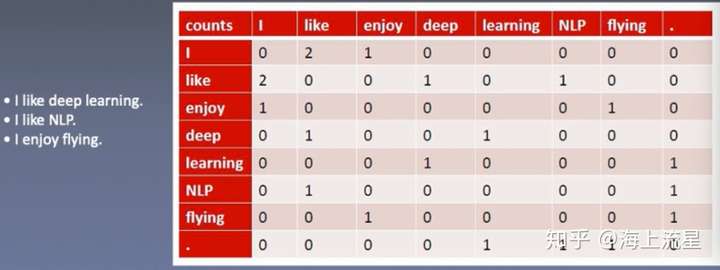
可以看到该矩阵中的共现频数,例如: 表示以
为中心词,
作为其上下文词的出现频数为2次;
表示以
为中心词,
作为其上下文词的出现频数为1次;
表示以
为中心词,
作为其上下文词的出现频数为1次;
定义符号
上面有介绍的共现矩阵元素 : 以
为中心词,
为语境词的频数。
共现矩阵中单词 那一行的和(即单词i所有语境词频数之和):
条件概率,表示单词 出现在单词
语境中(即所有语境词频数和中)的概率:
然后,我们关心的是—— 两个条件概率的比率(单词 分别出现在
和
这两个中心词语境中的概率之间的比值,一定程度上反映了单词
与单词
间语义和语法的相似性):
发现规律
作者发现该比率( )有一定规律,如下表所示:

那么,假设我们已经得到了词向量,如果用中心词词向量 、
和语境词词向量
,可以通过某种函数计算(表达)出
,且计算出的
符合上表中的规律的话,那么就意味着我们得到的词向量是与共现矩阵有很好的一致性(即词向量蕴含了共现矩阵中的信息)。
将词向量 、
、
计算ratio的函数设为
,先不考虑函数具体形式是什么,那么应该有:
即等式左边要与等式右边尽可能接近:
很容易想到用二者的均方误差来作为代价函数:
但是,代价函数中包含一个未知的函数 ,无法进行实际计算。且该未知函数包含3个单词词向量,这就意味着要在
的复杂度上进行计算,太复杂,最好能将代价函数进行参数简化。
推导代价函数
★构建
于是来考虑能否尝试构建出 的具体形式,并对参数个数和计算量上进行减少,作者是这样思考的:
1、要考虑单词 和单词
之间的关系,在线性空间中考察两个词向量的相似性,
大概是个合理的选择,
或许包含这一项;
2、 是个标量,那么
也应该是个标量,其输入都是词向量,那么使用内积应该是合理的选择,于是进一步构建出这么一项:
3、然后,为了让表达式更好地对应上除法,往 的外面套了一层指数运算
,得到最终的
★变换得到 的通用表达式
尝试构建出 的具体表达式后,就可以将上面的等式进行变换:
即:
这里,为了简化计算(虽然数学上不严谨),只需要让分子对应相等,分母对应相等,则等式成立(即 且
,于是我们就拿到了
(单词
出现在单词
语境中的概率)的通用表达式:
★简化后的代价函数
于是,我们的问题简化了,即本来我们的目标是追求 ,现在只需要让
尽可能成立就行了。
继续对上式进行变换,有个 还是不方便做计算的,容易出现特别大的数,于是对上式左右两边取对数,得到:
<center> </center>
那么代价函数就可以简化为:
目前这个代价函数就成功减少了参数(只有 和
两个词向量),且计算复杂度只有
了。
★为代价函数添加权重项
考虑到共现频率较低的词对,其相对重要性应该较低(共现次数很少的实际上可能是异常值,并且共现次数少的一般来说含的信息也少),因此在代价函数中应该添加权重项来相对弱化那些偶然才出现的词对关系,相对重视那些常出现的词对关系(但权重又不宜过高)。
于是我们构建一个基于 的权重函数
,该权重函数应该具备以下几个性质:
(1)如果单词i与j共现概率为0,那么这个词对不应该参与到代价函数中的计算中去,因此有 ;
(2)基于共现频率低权重低,共现频率高权重高的原则,权重函数对于 而言应该是非减的;
(3)在一个语料库中,肯定存在很多单词他们在一起出现的次数是很多的(frequent co-occurrences),但当共现频率过高时(这里人为设定一个频率阈值 ),权重不应过分增大;
因此,权重函数可以使用如下形式的分段函数:
这个函数在 取0.75时的图像如下所示:
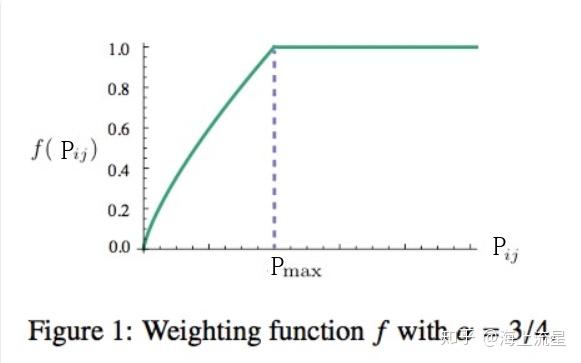
因此,添加了权重项的最终代价函数即为(1/2是为了方便优化时计算梯度):
最优化代价函数得到最终词向量矩阵
那么怎么最优化代价函数,进而得到我们要的 (中心词词向量矩阵)和
(上下文词词向量矩阵)两个词向量矩阵呢?
其实一样用的是:随机梯度下降(SGD),步骤如下。
(1)随机初始化
当然我们仍然需要随机初始化 和
两个矩阵(维度都为
,
为词向量维数,
为共现矩阵中的词数,
通常设置为300)的所有元素值。
(2)对共现矩阵X中非零元素进行随机抽样
(3)在一次抽样得到的词对 ,计算代价函数对于
和
的梯度(记为
和
)
其中 是可以直接通过共现矩阵中计算出来的,这一点在上面【定义符号】的part已经说明,因此由
可以计算出
和
。
(4)每一次抽样得到的词对 ,对
和
矩阵中的
列和
列进行更新(设定学习率为η)
(5)不断迭代随机抽样和 、
的更新,直至指定迭代次数(认为收敛),得到最终的词向量矩阵
和
(6)将 和
对应位置元素相加(或求平均)得到最终的词向量矩阵
从原理上讲 和
是对称的,他们唯一的区别是初始化的值不一样,而导致最终的值不一样。这两者其实是等价的,都可以当成最终的结果来使用。但是为了提高鲁棒性,我们最终会选择两者之和
作为最终的词向量矩阵(两者的初始化不同相当于加了不同的随机噪声,所以能提高鲁棒性)。