A:签到题
B!:搜索+DP

#include<bits/stdc++.h> #define mp make_pair #define pi pair<int,int> using namespace std; const int dx[4]={-1,1,0,0}; const int dy[4]={0,0,-1,1}; int f[60][60][60],v[60][60],a[60][60],bx,by,ex,ey,n,m,l; pi q[2000010]; char s[60]; void bfs(int k) { int h=1,r=0; for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) if (a[i][j]) { q[++r]=mp(i,j); v[i][j]=1; } while (h<=r) { int i=q[h].first,j=q[h].second; v[i][j]=0; h++; for (int w=0; w<4; w++) { int x=i+dx[w],y=j+dy[w]; if (!a[x][y]) continue; if (f[x][y][k]>f[i][j][k]+1) { f[x][y][k]=f[i][j][k]+1; if (!v[x][y]) { q[++r]=mp(x,y); v[x][y]=1; } } } } } int main() { scanf("%d%d",&n,&m); for (int i=1; i<=n; i++) { scanf("%s",s+1); for (int j=1; j<=m; j++) { if (s[j]!='#') a[i][j]=1; if (s[j]=='R') { bx=i; by=j; } if (s[j]=='E') { ex=i; ey=j; } } } scanf("%s",s+1); l=strlen(s+1); for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) for (int k=0; k<=l+1; k++) f[i][j][k]=1e9; int ans=1e9; f[bx][by][0]=0; for (int k=1; k<=l+1; k++) { bfs(k-1); ans=min(ans,f[ex][ey][k-1]); if (k==l+1) break; for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) if (a[i][j]) { int pw; if (s[k]=='L') pw=2; if (s[k]=='R') pw=3; if (s[k]=='U') pw=0; if (s[k]=='D') pw=1; int x=i+dx[pw],y=j+dy[pw]; if (a[x][y]) f[x][y][k]=min(f[i][j][k-1],f[x][y][k]); else f[i][j][k]=min(f[i][j][k-1],f[i][j][k]); f[i][j][k]=min(f[i][j][k-1]+1,f[i][j][k]); } } printf("%d ",ans); }
C:贪心 每次放尽量右边

#include <bits/stdc++.h> #define EPS 1.0e-9 #define PI acos(-1.0) #define INF 30000000 #define MOD 1000000007 #define mem(a,b) memset((a),b,sizeof(a)) #define TS printf("!!! ") #define pb push_back #define pai pair<int,int> //using ll = long long; //using ull= unsigned long long; //std::ios::sync_with_stdio(false); using namespace std; //priority_queue<int,vector<int>,greater<int>> que; typedef pair<int, int> pairint; typedef long long ll; typedef unsigned long long ull; const int maxn = 100005; ll mod = 1e9 + 7; int a[maxn]; int num[maxn]; int main() { // freopen("oddfactor.in", "r", stdin); // freopen("out.txt", "w", stdout); int n,k,r; int leftt; int rightt; leftt=rightt=1; int anser=0; int sum=0; mem(num,0); cin >> n >> k >> r; for(int i=1;i<=k;i++) { scanf("%d",&a[i]); num[a[i]]++; } for(int i=1;i<=n;i++) { if(num[i]) { if(sum) leftt=rightt,rightt=i+1; else rightt=i,sum++; } if(sum==0&&i-leftt==r-2) { rightt=i+1; anser++; sum++; } if(sum==1&&i-leftt==r-1) { leftt=rightt; rightt=i+1; anser++; } } cout<<anser<<endl; return 0; }
D!:首先假设做题顺序是i1,i2...in,那么最后罚时是n*t(i1)+(n-1)*t(i2)+...t(in)
考虑罚时的期望,根据期望的线性性质,如果第i道题期望在Pi时解决,那么它对期望的贡献就是(n-Pi)*ti
现在求所有可能罚时的总和,也就是我们只要求出每个题目的位置总贡献((n-Pi)*n!)即可
观察阅读规则,对于每道题什么时候读,我们只要考虑比这道题容易或难的题的数目
所以对第x道题,我们令f[i][j][p][r] 表示有i道比x简单的题还未读,j道比x难的题,p表示x有没有读,r表示当前读过r道比x简单的题,在这种情况下的位置总贡献
(耗时相同的我们随便假定一个难以顺序,因为我们只在乎最后总的贡献)
根据阅读规则很容易写出转移方程,具体见程序
又观察可得,在每个固定状态下,不论是针对哪道题,f[]是不变的即通用的,因此总的复杂度为O(n^3)

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int mo=1e9+7; int f[320][320][2][320]; ll d[320]; int a[320],n,k; void inc(int &a,int b) { a+=b; if (a>mo) a-=mo; } int dp(int i,int j,int p,int r) { if (f[i][j][p][r]!=-1) return f[i][j][p][r]; int s=-1,rr=r; if (i+j+p==0) s=k-r; //所有题都读过了 else if (i+j+p<=n-k) //读过的题超过了k道 { if (r) rr--; //先做最简单的 else if (p==0) s=(i+j+k)*d[i+j]%mo; //做当前考虑的这道并计算总的贡献 } if (s==-1) { s=0; //三种可能的读题情况 if (i) s=1ll*i*dp(i-1,j,p,rr+1)%mo; if (j) inc(s,1ll*j*dp(i,j-1,p,rr)%mo); if (p) inc(s,dp(i,j,p-1,rr)%mo); } f[i][j][p][r]=s; return s; } int main() { memset(f,255,sizeof(f)); d[0]=1; scanf("%d%d",&n,&k); for (int i=1; i<=n; i++) d[i]=d[i-1]*i%mo; for (int i=1; i<=n; i++) scanf("%d",&a[i]); sort(a+1,a+n+1); int ans=0; for (int i=1; i<=n; i++) ans=(ans+1ll*a[i]*dp(i-1,n-i,1,0)%mo)%mo; printf("%d ",ans); }
E!:
好题,首先求出原先控制区域的凸包
如果把问题一般化处理,就是求凸包插入一个点怎么变
对于每一颗新增点i,凸包面积如果发生变化,一定是从凸包上两点l,r连向i
i-r,i-l两条射线刚好能卡住原凸包,且原先凸包上l~r之间的点不再是边界
根据凸包面积计算公式,如果我们找到l,r,那么很容易用前缀和求出答案
为了寻找l,r,我们假定p1为凸包最左下的点,pm为凸包最右上的点
考虑i的位置,分4种情况
1. i在p1的左侧 2. i在pm的右侧
3. i在p1,pm之间且在p1,pm连线的上方
4. i在p1,pm之间且在p1,pm连线的下方
情况1和情况2类似且较为简单,l,r一定分别在凸包的上凸壳和下凸壳上(也可能正好是p1,pm)
根据i-r,i-l两条射线刚好能卡住原凸包的性质可以用二分快速找到
情况3和情况4显然,l,r会同时落在上凸壳或下凸壳上,我们需要找到一个凸包的分界点k
使得x[k-1]<x[i]<=x[k],这显然是可以用二分求出的,再在上(下)凸壳的左右区间分别用二分找到l,r即可
示意图如下:
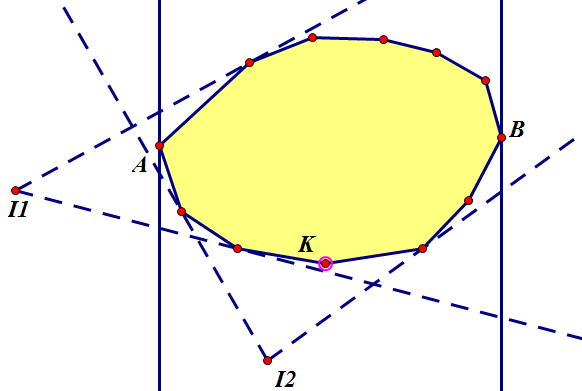
其实,还有一个更简单的方法
可以证明,如果要是新的凸包面积最大,那么增加的点应在整个点集的凸包上
随着点在凸包上的逆时针(或顺时针移动),其对应的l,r也在凸包上做同向移动,由此就是two pointer的问题了
但是写起来似乎很有细节问题,改日把这个方法补上
另外注意这题答案会很大,double精度不够,又答案只有一位小数,直接判断着输出即可

#include<bits/stdc++.h> using namespace std; typedef long long ll; struct po { int x,y; friend bool operator <(po a,po b) { if (a.x==b.x) return a.y<b.y; return a.x<b.x; } friend po operator -(po a,po b) { return (po){a.x-b.x,a.y-b.y}; } friend po operator +(po a,po b) { return (po){a.x+b.x,a.y+b.y}; } friend ll operator *(po a, po b) { return 1ll*a.x*b.y-1ll*a.y*b.x; } } p[100010],q[100010]; int n,k,t; ll s[100010]; int get(int l,int r,int i,int w) { while (l<r) { int m=(l+r)>>1; if ((q[m]-p[i])*(q[m+1]-p[i])*w>0) r=m; else l=m+1; } return l; } int bord(int l,int r,int i,int w) { while (l<r) { int m=(l+r)>>1; if ((q[m].x-p[i].x)*w<0) l=m+1; else r=m; } return l; } int main() { scanf("%d%d",&n,&k); for (int i=1; i<=n; i++) scanf("%d%d",&p[i].x,&p[i].y); sort(p+1,p+1+k); q[1]=p[1]; t=1; for (int i=2; i<=k; i++) { while (t>1&&(p[i]-q[t-1])*(q[t]-q[t-1])>=0) t--; q[++t]=p[i]; } int m=t; for (int i=k-1;i;i--) { while (t>m&&(p[i]-q[t-1])*(q[t]-q[t-1])>=0) t--; q[++t]=p[i]; } for (int i=1; i<t; i++) s[i+1]+=s[i]+q[i]*q[i+1]; ll ans=s[t],tmp; for (int i=k+1; i<=n; i++) { if (p[i].x<q[1].x) { int l=get(1,m,i,1), r=get(m,t,i,-1); tmp=s[r]-s[l]+q[r]*p[i]+p[i]*q[l]; } else if (p[i].x>q[m].x) { int l=get(1,m,i,-1),r=get(m,t,i,1); tmp=s[t]-s[r]+s[l]+q[l]*p[i]+p[i]*q[r]; } else if ((q[m]-q[1])*(p[i]-q[1])>0) { int mid=bord(m,t,i,-1); if (mid>m&&(q[mid]-q[mid-1])*(p[i]-q[mid-1])>0) continue; int l=mid>m?get(m,mid-1,i,-1):m; int r=get(mid,t,i,1); tmp=s[t]-s[r]+s[l]+q[l]*p[i]+p[i]*q[r]; } else { int mid=bord(1,m,i,1); if (mid>1&&(q[mid]-q[mid-1])*(p[i]-q[mid-1])>0) continue; int l=(mid>1)?get(1,mid-1,i,-1):1; int r=get(mid,m,i,1); tmp=s[t]-s[r]+s[l]+q[l]*p[i]+p[i]*q[r]; } ans=max(ans,tmp); } printf("%lld",ans/2); if (ans&1) puts(".5"); else puts(".0"); } 方法一
F:2-sat问题

#include <bits/stdc++.h> #define MAXN 10005 using namespace std; struct TwoSat{ int dfn[MAXN * 2], low[MAXN * 2], dfs_ind = 1, sccno[MAXN * 2], scc_cnt = 0, w[MAXN * 2]; vector<int> G[MAXN * 2]; stack<int> st; void Add(int u, int v) { G[u].push_back(v); } void Tarjan(int u) { dfn[u]=low[u]=dfs_ind++; st.push(u); for(int i=0; i < G[u].size(); i++) { int v = G[u][i]; if(!dfn[v]) { Tarjan(v); low[u]=min(low[u],low[v]); }else if(!sccno[v]) { low[u]=min(low[u],dfn[v]); } } if(dfn[u]==low[u]) { scc_cnt++; while(true) { int x=st.top();st.pop(); sccno[x]=scc_cnt; w[scc_cnt]++; if(x==u)break; } } } bool Solve(int m) { for(int i = 1; i <= m * 2; i++) { if(!dfn[i]) { while(!st.empty())st.pop(); Tarjan(i); } } for(int i = 1; i <= m; i++){ if(sccno[i] == sccno[i + m]) { return false; } } return true; } }twosat; int n, r, l, x[MAXN], y[MAXN]; int main() { scanf("%d%d%d", &n, &r, &l); for(int i = 1; i <= l; i++) { scanf("%d%d", &x[i], &y[i]); } for(int i = 1; i <= l; i++) { for(int j = 1; j <= l; j++) { if(i == j) continue; if(x[i] == x[j] && abs(y[i] - y[j]) <= 2 * r) { twosat.Add(i + l, j); twosat.Add(j + l, i); } if(y[i] == y[j] && abs(x[i] - x[j]) <= 2 * r) { twosat.Add(i, j + l); twosat.Add(j, i + l); } } } if(twosat.Solve(l)) { printf("YES "); }else { printf("NO "); } return 0; }
G!:首先把确定的拎出来,不确定的地方要使海岛尽可能多,那必定是将一格作为一个海岛
不难想到将图黑白染色做而二分图的最大独立集

#include<bits/stdc++.h> using namespace std; const int dx[4]={-1,1,0,0}; const int dy[4]={0,0,-1,1}; char s[100]; int f[1610],b[60][60],a[60][60],v[60][60],cy[1610],cx[1610],n,m,ans,t; vector<int> g[1610]; void dfs(int i,int j) { v[i][j]=1; for (int k=0; k<4; k++) { int x=i+dx[k],y=j+dy[k]; if (x==0||x>n||y>m||y==0) continue; if (v[x][y]) continue; if (a[x][y]==-1) a[x][y]=0; if (a[x][y]==1) dfs(x,y); } } int work(int x) { for (int i=0; i<g[x].size(); i++) { int y=g[x][i]; if (!f[y]) { f[y]=1; if (!cy[y]||work(cy[y])) { cx[x]=y; cy[y]=x; return 1; } } } return 0; } int main() { //freopen("1.in","r",stdin); scanf("%d%d",&n,&m); for (int i=1; i<=n; i++) { scanf("%s",s+1); for (int j=1; j<=m; j++) { if (s[j]=='W') a[i][j]=0; if (s[j]=='C') a[i][j]=-1; if (s[j]=='L') a[i][j]=1; } } for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) if (!v[i][j]&&a[i][j]==1) { ans++; dfs(i,j); } for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) if (a[i][j]==-1) b[i][j]=++t; for (int i=1; i<=n; i++) for (int j=1; j<=m; j++) if ((i+j)%2==0) { for (int k=0; k<4; k++) { int x=i+dx[k],y=j+dy[k]; if (b[x][y]) g[b[i][j]].push_back(b[x][y]); } } int s=0; for (int i=1; i<=t; i++) if (g[i].size()) { if (!cx[i]) { memset(f,0,sizeof(f)); s+=work(i); } } printf("%d ",ans+t-s); }
H:离散化后DP ans[i]表示取i个最少要漏掉多少个 不取的话就直接duan[i].r-duan[i-1].r取的话就duan[i].l-duan[cur].r-1

#include <bits/stdc++.h> #define EPS 1.0e-9 #define PI acos(-1.0) #define INF 30000000 #define MOD 1000000007 #define mem(a,b) memset((a),b,sizeof(a)) #define TS printf("!!! ") #define pb push_back #define pai pair<int,int> //using ll = long long; //using ull= unsigned long long; //std::ios::sync_with_stdio(false); using namespace std; //priority_queue<int,vector<int>,greater<int>> que; typedef pair<int, int> pairint; typedef long long ll; typedef unsigned long long ull; const int maxn = 200005; ll mod = 1e9 + 7; struct node { ll l; ll r; }duan[maxn]; ll righ[maxn]; ll ans[maxn]; ll getit[maxn]; bool cmp(node a,node b) { return b.r>a.r; } int main() { // freopen("oddfactor.in", "r", stdin); // freopen("out.txt", "w", stdout); ll n,m; ll anser; ll cur; cin >> n >> m; for(int i=1;i<=m;i++) scanf("%lld %lld",&duan[i].l,&duan[i].r); sort(duan+1,duan+1+m,cmp); ll now=0; for(int i=1;i<=m;i++) righ[i]=duan[i].r; for(int i=1;i<=m;i++) { cur=lower_bound(righ+1,righ+1+m,duan[i].l)-righ-1; ans[i]=min(ans[cur]+duan[i].l-duan[cur].r-1,ans[i-1]+duan[i].r-duan[i-1].r); } cout<<n+ans[m]-duan[m].r; return 0; }
I:贪心 每次肯定送尽可能最远的最优

#include<math.h> #include<string.h> #include<iostream> #include<algorithm> #include<sstream> //istringstream stm(string); stm >> x; #include<vector> #define INF 2139062143 #define inf -2139062144 #define ll long long using namespace std; struct point { ll pos,letter; }; bool cmp(point p1, point p2) { return p1.pos < p2.pos; } vector<point> pzheng,pfu; int main() { ll n,k,i,j; scanf("%lld%lld",&n,&k); for(i=0; i<n; i++) { ll pos,x; scanf("%lld%lld",&pos,&x); if(pos >= 0) { pzheng.push_back({pos,x}); } else { pfu.push_back({-pos,x}); } } sort(pzheng.begin(),pzheng.end(),cmp); sort(pfu.begin(),pfu.end(),cmp); // for(i=0;i<pzheng.size();i++){ // printf("%lld %lld ",pzheng[i].pos,pzheng[i].letter); // } bool over = false; ll size = pzheng.size(); ll cur = size - 1; ll ans = 0; if(size > 0) { while(!over) { if(pzheng[cur].letter > k) { ll time = pzheng[cur].letter / k; ans += time * pzheng[cur].pos * 2; pzheng[cur].letter -= time * k; if(pzheng[cur].letter == 0) cur--; } else { ll send = k; ans += 2 * pzheng[cur].pos; while(send > 0 && cur >= 0) { ll last = pzheng[cur].letter; pzheng[cur].letter = max((ll)0,pzheng[cur].letter - send); send -= (last - pzheng[cur].letter); if(send > 0 || pzheng[cur].letter == 0) { cur--; } } } if(pzheng[0].letter == 0 || cur < 0) { over = true; } } } over = false; size = pfu.size(); if(size > 0) { cur = size - 1; while(!over) { if(pfu[cur].letter > k) { ll time = pfu[cur].letter / k; ans += time * pfu[cur].pos * 2; pfu[cur].letter -= time * k; if(pfu[cur].letter == 0) cur--; } else { ll send = k; ans += 2 * pfu[cur].pos; while(send > 0 && cur >= 0) { ll last = pfu[cur].letter; pfu[cur].letter = max((ll)0,pfu[cur].letter - send); send -= (last - pfu[cur].letter); if(send > 0 || pfu[cur].letter == 0) { cur--; } } } if(pfu[0].letter == 0 || cur < 0) { over = true; } } } printf("%lld ",ans); return 0; }
J:2016年网络赛题

#include <bits/stdc++.h> #define EPS 1.0e-9 #define PI acos(-1.0) #define INF 30000000 #define MOD 1000000007 #define mem(a,b) memset((a),b,sizeof(a)) #define TS printf("!!! ") #define pb push_back #define pai pair<int,int> //using ll = long long; //using ull= unsigned long long; //std::ios::sync_with_stdio(false); using namespace std; //priority_queue<int,vector<int>,greater<int>> que; typedef pair<int, int> pairint; typedef long long ll; typedef unsigned long long ull; const int maxn = 200005; int n,m; ll aaa[maxn][20]; ll a[maxn]; void init() { for(int i=1;(1<<i)<=n;i++) for(int j=1;j<=n-(1<<i)+1;j++) { aaa[j][i]=min(aaa[j][i-1],aaa[j+(1<<(i-1))][i-1]); } } ll runit(int l,int r) { int now; for(now=0;(1<<now)<=r-l+1;now++); now--; ll ans=min(aaa[l][now],aaa[r-(1<<now)+1][now]); return ans; } int cal(ll value,int x,int y) { if(x>y) return 0; if(value>a[x]) return x; if(x==y) return 0; if(value<runit(x,y)) return 0; int l=x,r=y,mid; while(r-l>1) { mid=(l+r)/2; if(value>=runit(x,mid)) r=mid; else l=mid; } return r; } ll work(ll pop,int pop1,int pop2) { int flag=1; while(flag) { pop%=a[pop1]; int now=cal(pop,pop1+1,pop2); if(!now) return pop; else pop1=now; } } int main() { cin >> n >> m; for(int i=1;i<=n;i++) { scanf("%I64d",&a[i]); aaa[i][0]=a[i]; } init(); while(m--) { ll cur,l,r; scanf("%I64d %I64d %I64d",&cur,&l,&r); //cin >> cur >> l >> r //cout<<cur<<" "<<l<<" "<<r<<endl; printf("%I64d ",work(cur,l,r)); } return 0; }
