一、基本概念
评价指标是针对模型性能优劣的一个定量指标。
一种评价指标只能反映模型一部分性能,如果选择的评价指标不合理,那么可能会得出错误的结论,故而应该针对具体的数据、模型选取不同的的评价指标。
本文将详细介绍机器学习分类任务的常用评价指标:混淆矩阵(Confuse Matrix)、准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1 Score、P-R曲线(Precision-Recall Curve)、ROC、AUC。
二、混淆矩阵(Confuse Matrix)
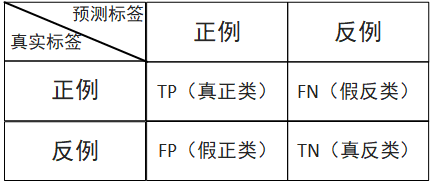
针对一个二分类问题,即将实例分成正类(positive)或负类(negative),在实际分类中会出现以下四种情况:
(1)若一个实例是正类,并且被预测为正类,即为真正类TP(True Positive )
(2)若一个实例是正类,但是被预测为负类,即为假负类FN(False Negative )
(3)若一个实例是负类,但是被预测为正类,即为假正类FP(False Positive )
(4)若一个实例是负类,并且被预测为负类,即为真负类TN(True Negative )
混淆矩阵的每一行是样本的预测分类,每一列是样本的真实分类(反过来也可以)。
三、准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1 Score
1.准确率(Accuracy)
预测正确的样本数量占总量的百分比,具体的公式如下:
$Accuracy=frac{TP+TN}{TP+FN+FP+TN}$
准确率有一个缺点,就是数据的样本不均衡,这个指标是不能评价模型的性能优劣的。
假如一个测试集有正样本99个,负样本1个。模型把所有的样本都预测为正样本,那么模型的Accuracy为99%,看评价指标,模型的效果很好,但实际上模型没有任何预测能力。
2.精准率(Precision)
又称为查准率,是针对预测结果而言的一个评价指标。在模型预测为正样本的结果中,真正是正样本所占的百分比,具体公式如下:
$Accuracy=frac{TP}{TP+FP}$
精准率的含义就是在预测为正样本的结果中,有多少是准确的。这个指标比较谨慎,分类阈值较高。
3.召回率(Recall)
又称为查全率,是针对原始样本而言的一个评价指标。在实际为正样本中,被预测为正样本所占的百分比。具体公式如下:
$Accuracy=frac{TP}{TP+FN}$
尽量检测数据,不遗漏数据,所谓的宁肯错杀一千,不肯放过一个,分类阈值较低。
4.F1 Score
针对精准率和召回率都有其自己的缺点;如果阈值较高,那么精准率会高,但是会漏掉很多数据;如果阈值较低,召回率高,但是预测的会很不准确。
例子一
假设总共有10个好苹果,10个坏苹果。针对这20个数据,模型只预测了1个好苹果,对应结果如下表

$ Precision=frac{1}{1+0}=1$
$ Recall=frac{1}{1+8}=0.1$
虽然精确率很高,但是这个模型的性能并不好。
例子二
同样总共有10个好苹果,10个坏苹果。针对这20个数据,模型把所有的苹果都预测为好苹果,对应结果如下表
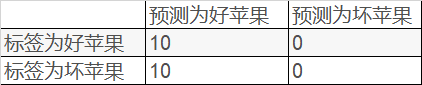
$Precision=frac{10}{10+10}=0.5$
$Recall=frac{10}{10+0}=1$
虽然召回率很高,但是这个模型的性能并不好。
从上述例子中,可以看到精确率和召回率是此消彼长的,如果要兼顾二者,就需要F1 Score。
$ F1=frac{2×P×R}{P+R}$
F1 Score是一种调和平均数。
四、P-R曲线
P-R曲线是描述精确率和召回率变化的曲线。对于所有的正样本,
绘制P-R曲线
设置不同的阈值,模型预测所有的正样本,计算对应的精准率和召回率。

模型与坐标轴围成的面积越大,则模型的性能越好。但一般来说,曲线下的面积是很难进行估算的,所以衍生出了“平衡点”(Break-Event Point,简称BEP),即当P=R时的取值,平衡点的取值越高,性能更优。
五、ROC曲线和AUC
1.为什么会有ROC?
例子三
有好苹果9个,坏苹果1个,模型把所有的苹果均预测为好苹果。

$Accuracy=frac{9}{9+1}=0.9$
$Precision=frac{9}{9+1}=0.9$
$Recall=frac{9}{9+0}=1$
$ F1=frac{2×P×R}{P+R}=frac{2×0.9×1}{1+0.9}=frac{1.8}{1.9}approx 1$
我们能够得出,尽管 Precision、Recall、F1都很高,但是模型效果却不好。所以针对样本不均衡,以上指标很难区分模型的性能,就需要用到ROC和AUC。因为对于Precision、Recall、F1仅仅是通过正类计算得到,而ROC曲线在负类上也有计算,故而模型误分类负样本,在指标上有所体现,所以虽然正样本多,负样本少,也可以判断模型的性能。所以AUC不受类别不平衡问题的影响。
2.基本概念
对应的各个缩写含义:

在介绍ROC和AUC之前,我们需要明确以下三个概念:
真正类率(true positive rate, TPR),也称为灵敏度(sensitivity),等同于召回率。刻画的是被分类器正确分类的正实例占所有正实例的比例。
$TPR=frac{正样本预测正确量}{正样本总量}=frac{TP}{TP+FN}$
真负类率(true negative rate, TNR),也称为特异度(specificity),刻画的是被分类器正确分类的负实例占所有负实例的比例。
$TNR = frac{负样本预测正确量}{负样本总量}= frac{TN}{FP+TN}$
假正类率(false positive rate, FPR),也称为1-specificity,计算的是被分类器错认为正类的负实例占所有负实例的比例。
$FPR =1 - TNR=frac{负样本预测错误量}{负样本总量}=frac{FP}{FP+TN}$
3.ROC曲线
ROC(Receiver Operating Characteristic)曲线,又称接受者操作特征曲线。曲线对应的纵坐标是TPR,横坐标是FPR。
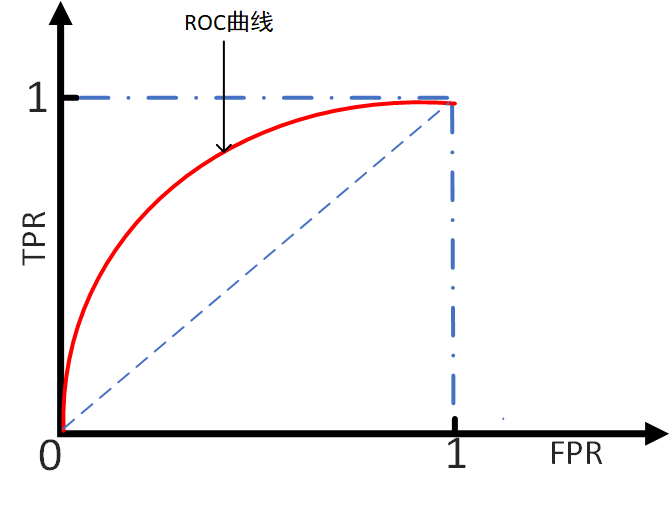
绘制方法:
设置不同的阈值,会得到不同的TPR和FPR,而随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着负类,即TPR和FPR会同时增大。阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1)。
理想目标: TPR=1, FPR=0,即图中(0,1)点。故ROC曲线越靠拢(0,1)点,即,越偏离45度对角线越好。对应的就是TPR越大越好,FPR越小越好。
4.AUC
AUC(Area Under Curve)是处于ROC曲线下方的那部分面积的大小。AUC越大,代表模型的性能越好。
对于例子三的样本不均衡,对应的TPR=1,而FPR=1,能够判断模型性能不好。
auc的计算
auc就是:随机抽出一对样本(一个正样本,一个负样本),然后用训练得到的分类器来对这两个样本进行预测,预测得到正样本的概率大于负样本概率的概率。
在有M个正样本,N个负样本的数据集里。一共有M*N对样本(一对样本即,一个正样本与一个负样本)。统计这M*N对样本里,正样本的预测概率大于负样本的预测概率的个数。
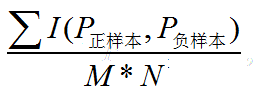
举个例子:
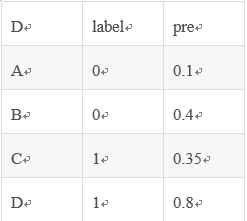
假设有4条样本。2个正样本,2个负样本,那么M*N=4。
即总共有4个样本对。分别是:
(D,B),(D,A),(C,B),(C,A)。
在(D,B)样本对中,正样本D预测的概率大于负样本B预测的概率(也就是D的得分比B高),记为1
同理,对于(C,B)。正样本C预测的概率小于负样本C预测的概率,记为0.
那么auc如下:
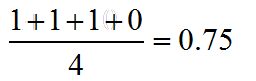
具体代码:
def naive_auc(labels,preds): """ 最简单粗暴的方法 先排序,然后统计有多少正负样本对满足:正样本预测值>负样本预测值, 再除以总的正负样本对个数 复杂度 O(NlogN), N为样本数 """ n_pos = sum(labels) n_neg = len(labels) - n_pos total_pair = n_pos * n_neg labels_preds = zip(labels,preds) #按照概率排序,大的在前 labels_preds = sorted(labels_preds,key=lambda x:x[1]) accumulated_neg = 0 satisfied_pair = 0 for i in range(len(labels_preds)): if labels_preds[i][0] == 1: #统计在当前的概率下,计算大于当前概率负类的个数, satisfied_pair += accumulated_neg else: accumulated_neg += 1 return satisfied_pair / float(total_pair)
总结
当正负样本差距不大的情况下,ROC和PR的趋势是差不多的,但是当负样本很多的时候,两者就截然不同了,ROC效果依然看似很好,但是PR上反映效果一般。ROC就不会出现例子一、二、三的情况。
参考:
https://www.cnblogs.com/guoyaohua/p/classification-metrics.html
https://blog.csdn.net/manduner/article/details/91040867
https://blog.csdn.net/chocolate_chuqi/article/details/81162244