小波变换能够很好地表征一大类以低频信息为主要成分的信号,
小波包变换可以对高频部分提供更精细的分解
详见(http://www.cnblogs.com/welen/articles/5667217.html)
小波分解函数和重构函数的应用和区别
(https://www.baidu.com/link?url=NsLWcGxYPabqB0JEFzkjHzeLmcvGkjDRccPoaD7K0gwo9mrHRDCUgTbV15zT8NKTm9PAuTJ2Hwb3n10PutFRpbOdQRac7XC48fI2uYmA2eC&wd=&eqid=bae463400004bb3f000000035c0cc2a9)
小波分析基本函数可分为分解和重构两类.
一维小波分解函数和系数提取函数:
对常用的dwt、wavedec、appcoef函数的常用格式进行举例说明。
格式: [ca, cd]=dwt(X,’wname’) %单尺度一维离散小波分解
[C, L]=wavedec(X,N,’wname’) %多尺度一维小波分解(多分辨分析函数)
ca=appcoef(C,L,’wname’,N) %提取一维小波变换低频系数
说明:
(1)小波分解函数和系数提取函数的结果都是分解系数;
(2)如何理解小波系数:小波系数是信号在做小波分解时所选择的小波函数空间的投影。
我们知道,一个信号可以分解为傅里叶级数,即一组三角函数之和,而傅里叶变换对应于傅里叶级数的系数;同样,一个信号可以表示为一组小波基函数之和,小波变换系数就对应于这组小波基函数的系数。
(3)多尺度分解是按照多分辨分析理论,分解尺度越大,分解系数的长度越小(是上一个尺度的二分之一)。我们会发现分解得到的小波低频系数的变化规律和原始信号相似,但要注意低频系数的数值和长度与原始信号以及后面重构得到的各层信号是不一样的。
一维小波重构函数:
对常用的idwt、waverec、wrcoef函数进行举例说明。
格式:
- X=idwt(ca,cd,’wmane’) %单尺度一维小波逆变换
- X=waverec(C,L,’wname’) %多尺度一维小波重构
- X=wrcoef(‘type’,C,L,’wname’,N) %对一维小波系数进行单支重构
说明:
(1) 小波重构函数的结果都是信号;
(2) 不管是用哪个重构函数对系数进行重构后,结果的长度和原始信号的长度是相同的;
如果重构的是低频部分,那么观察得到的结果X,其数值大小和原始信号是差不多的。
(其他参考:
https://www.baidu.com/link?url=Op4W9vNERXYnf25eqkDqywDdzN_J_6jJrZPi1DgK_uFkD3Jzbcfv41bu6dPSnCgg0lMKnES9qsIppG7Q95_RVOyotqEU2cTnkj1FkH5-c1a&wd=&eqid=bae463400004bb3f000000035c0cc2a9
https://blog.csdn.net/chenyusiyuan/article/details/2514119)
小波去噪:
一般来说,噪声信号多包含在具有较高频率细节中,在对信号进行了小波分解之后,再利用门限阈值等形式对所分解的小波系数进行权重处理,然后对小信号再进行重构即可达到信号去噪的目的。具体步骤为:
a.一维信号的小波分解,选择一个小波并确定分解的层次,然后进行分解计算。
b.小波分解高频系数的阈值量化,对各个分解尺度下的高频系数选择一个阈值进行软阈值量化处理。
C.一维小波重构,根据小波分解的最底层低频系数和各层高频系数进行一维小波的重构
一维小波变换的 Matlab 实现(https://blog.csdn.net/qq_29543611/article/details/80232662)
(1) dwt 函数
功能:一维离散小波变换
格式:[cA,cD]=dwt(X,'wname')
[cA,cD]=dwt(X,Lo_D,Hi_D)
说明:[cA,cD]=dwt(X,'wname') 使用指定的小波基函数 'wname' 对信号 X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数
功能:一维离散小波反变换
格式:X=idwt(cA,cD,'wname')
X=idwt(cA,cD,Lo_R,Hi_R)
X=idwt(cA,cD,'wname',L)
X=idwt(cA,cD,Lo_R,Hi_R,L)
说明:X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname' 为所选的小波函数
X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和 Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,'wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。
其他资料:
http://blog.sina.com.cn/s/blog_b526d0f10102xxh6.html
https://blog.csdn.net/charlene_bo/article/details/71156390
https://blog.csdn.net/ckzhb/article/details/78288847
小波包分解和小波分解:(https://blog.csdn.net/ckzhb/article/details/78288847)
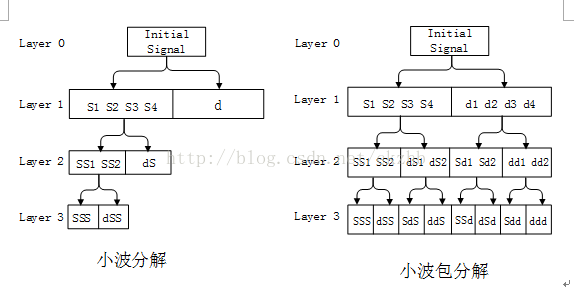
能量谱:(https://blog.csdn.net/ckzhb/article/details/78288847 )
基于小波包分解提取多尺度空间能量特征的原理是把不同分解尺度上的信号能量求解出来,将这些能量值按尺度顺序排列成特征向量供识别使用。
20180510补充更新:具体计算公式如下所示,本文中未使用重构后的系数进行能量值计算,直接使用小波包分解后的系数,参考文献《基于小波包能量特征的滚动轴承故障监测方法 》。

给出两部分代码,写成两个函数。一个是小波包分解与重构,另一个是能量谱函数。
下载地址:https://download.csdn.net/download/ckzhb/10030651
代码名称:wavelet_packetdecomposition_reconstruct
https://blog.csdn.net/qq_23869697/article/details/79436808