接上一个....
小波变换(https://www.zhihu.com/question/22864189/answer/40772083)
STFT是给信号加窗,分段做FFT;而小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间了
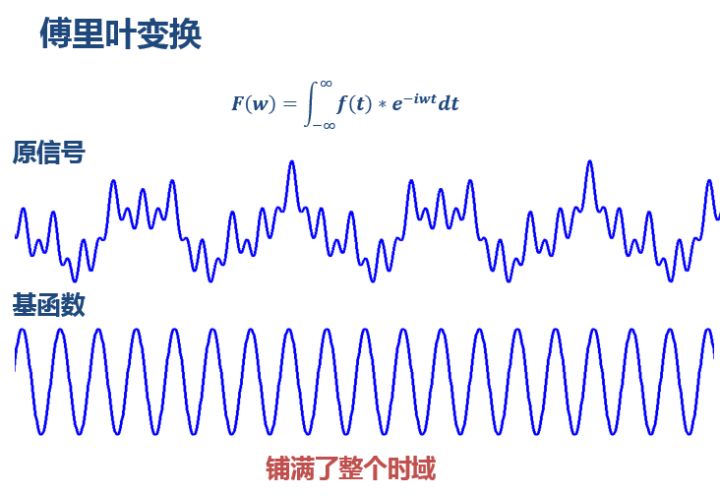
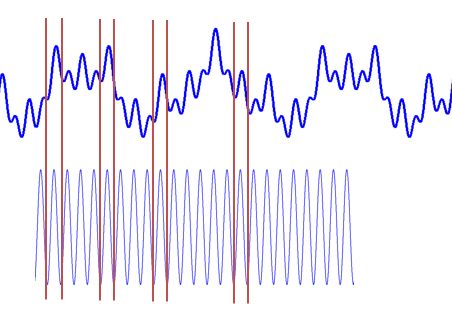
这个基函数会伸缩、会平移(其实本质并非平移,而是两个正交基的分解)。缩得窄,对应高频;伸得宽,对应低频。然后这个基函数不断和信号做相乘。某一个尺度(宽窄)下乘出来的结果,就可以理解成信号所包含的当前尺度对应频率成分有多少。于是,基函数会在某些尺度下,与信号相乘得到一个很大的值,因为此时二者有一种重合关系。那么我们就知道信号包含该频率的成分的多少。 仔细体会可以发现,这一步其实是在计算信号和三角函数的相关性。
看,这两种尺度能乘出一个大的值(相关度高),所以信号包含较多的这两个频率成分,在频谱上这两个频率会出现两个峰。 以上,就是粗浅意义上傅里叶变换的原理。
如前边所说,小波做的改变就在于,将无限长的三角函数基换成了有限长的会衰减的小波基。

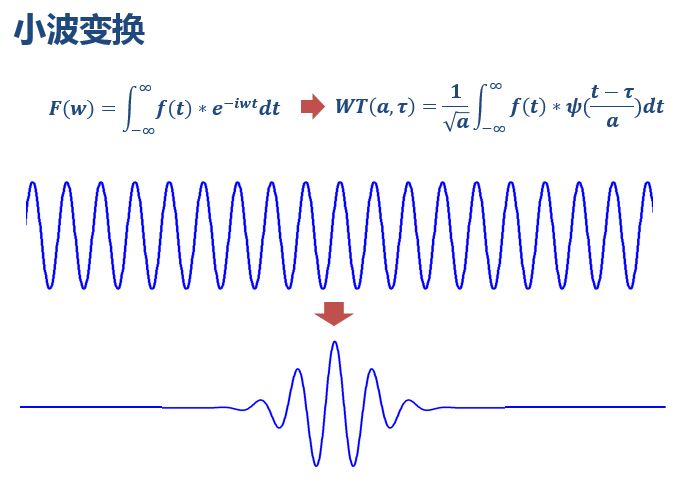
从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函数的伸缩,平移量 τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。
当伸缩、平移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。 而当我们在每个尺度下都平移着和信号乘过一遍后,我们就知道信号在每个位置都包含哪些频率成分。 看到了吗?有了小波,我们从此再也不害怕非稳定信号啦!从此可以做时频分析啦! 做傅里叶变换只能得到一个频谱,做小波变换却可以得到一个时频谱!
时域信号 傅里叶变换结果 小波变换结果
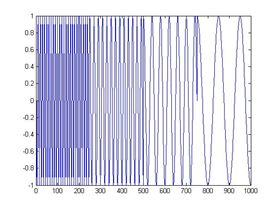
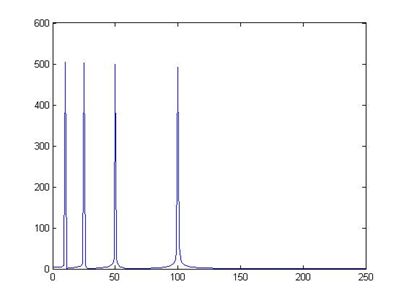
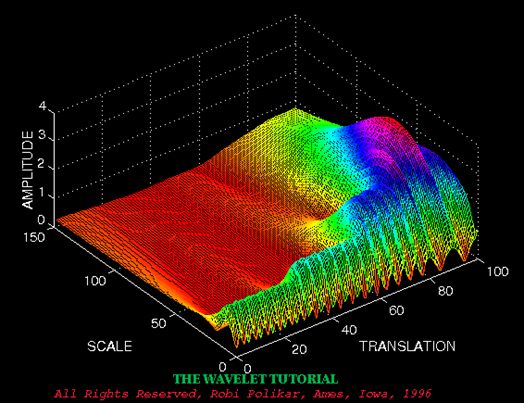
小波还有一些好处,比如,我们知道对于突变信号,傅里叶变换存在吉布斯效应,我们用无限长的三角函数怎么也拟合不好突变信号:
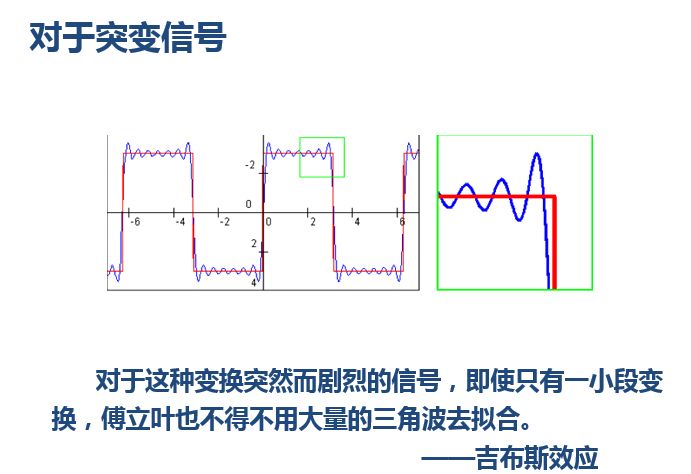
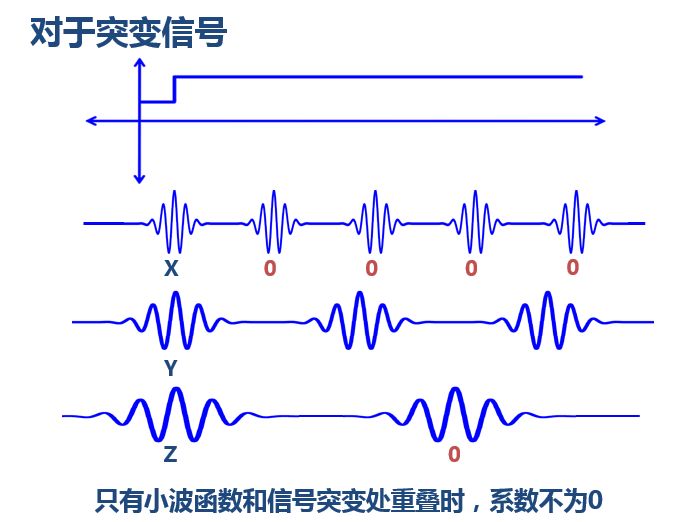
每个小波变换都会有一个mother wavelet,我们称之为母小波,同时还有一个father wavelet,就是scaling function。而该小波的basis函数其实就是对这个母小波和父小波缩放和平移形成的。缩放倍数都是2的级数,平移的大小和当前其缩放的程度有关。
小波级数通常是orthonormal basis,也就是说,它们不仅两两正交,还归一化了。
一般小波变换的三个特点,就是小波级数是二维的,能定位时域和频域,计算很快
(补充:https://www.cnblogs.com/h2zZhou/p/8405717.html 傅里叶动图)
补充材料:
https://www.cnblogs.com/jfdwd/p/9249850.html
https://www.baidu.com/link?url=RUJReijcKg_zaKkwO6BWHZbaq2KfFsgiEK0jyqGZxjlrDg1_vVOPwnADHdNiIi4XQvTyUoep89pC-T7KJhta-7UHxOmMpAOF27ymjXzlBCK&wd=&eqid=93c0521a000e1bd2000000035c0bbd8e
https://www.baidu.com/link?url=eNTvMgLhxpxhXZCT0phkIDs505UtueP8b2p_SESCUeBG6T0Ie0ECVYdsQBosWSitv8fs52DRd62YdYtFHiFZlb-ZZxZu3PmKFitgbvIoRDm&wd=&eqid=93c0521a000e1bd2000000035c0bbd8e
https://blog.csdn.net/yq_forever/article/details/55253022