本章介绍了快速排序及其算法分析,快速排序采用的是分治算法思想,对包含n个数的输入数组,最坏情况下运行时间为θ(n^2),但是平均性能相当好,期望的运行时间为θ(nlgn)。另外快速排序能够就地排序(我理解是不需要引入额外的辅助空间,每次划分能确定一个元素的具体位置),在虚拟环境中能很好的工作。
1、快速排序的描述
快速排序算法采用的分治算法,因此对一个子数组A[p…r]进行快速排序的三个步骤为:
(1)分解:数组A[p...r]被划分为两个(可能为空)子数组A[p...q-1]和A[q+1...r],给定一个枢轴,使得A[p...q-1]中的每个元素小于等于A[q],A[q+1...r]中的每个元素大于等于A[q],q下标是在划分过程中计算得出的。
(2)解决:通过递归调用快速排序,对子数组A[p...q-1]和A[q+1...r]进行排序。
(3)合并:因为两个子数组是就地排序,不需要合并操作,整个数组A[p…r]排序完成。
快速排序关键过程是对数组进行划分,划分过程需要选择一个主元素(pivot element)作为参照,围绕着这个主元素进划分子数组。举个列说明如何划分数组,现有子数组A={24,15,27,5,43,87,34},以最后一个元素为主元素进行划分,划分过程如图所示: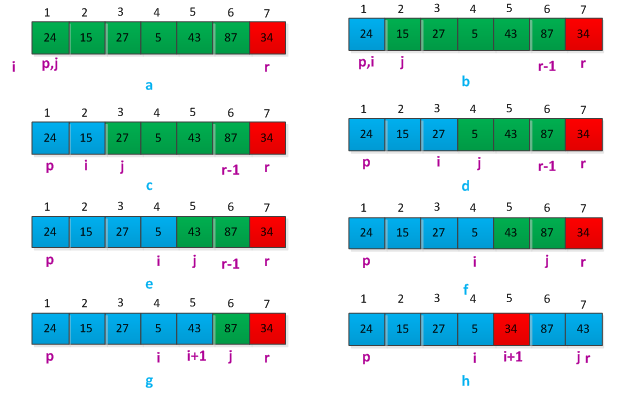
书中给出了划分过程的伪代码:
1 PARTITION(A,p,r) 2 x = A[r] //将最后一个元素作为主元素 3 i = p-1 4 for j=p to r-1 //从第一个元素开始到倒数第二个元素结束,比较确定主元的位置 5 do if A[j] <= x 6 i = i+1 7 exchange A[i] <-> A[j] 8 exchange A[i+1]<->A[r] //最终确定主元的位置 9 return i+1 //返回主元的位置
根据划分过程的为代码,书中又给出了快速排序的为代码:
1 QUICKSORT(A,p,r) 2 if p<r 3 q = PARTITION(A,p,r) //确定划分位置 4 QUICKSORT(A,p,q-1) //子数组A[p...q-1] 5 QUICKSORT(Q,q+1,r) //子数组A[q+1...r]
采用C元素实现一个完成的快速排序程序,程序如下:
 View Code
View Code
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 size_t partition(int* datas,int beg,int last); 5 void quick_sort(int* datas,int beg,int last); 6 void swap(int *a,int *b); 7 8 int main() 9 { 10 size_t i; 11 int datas[10] = {78,13,9,23,45,14,35,65,56,79}; 12 printf("After quick sort,the datas is:\n"); 13 quick_sort(datas,0,9); 14 for(i=0;i<10;++i) 15 printf("%d ",datas[i]); 16 exit(0); 17 } 18 19 void swap(int *a,int *b) 20 { 21 int temp = *a; 22 *a = *b; 23 *b = temp; 24 } 25 26 size_t partition(int* datas,int beg,int last) 27 { 28 int pivot = datas[last]; 29 int i,j; 30 i = beg -1; 31 for(j=beg;j<last;j++) 32 { 33 if(datas[j] < pivot) 34 { 35 i = i+1; 36 swap(datas+i,datas+j); 37 } 38 } 39 swap(datas+i+1,datas+last); 40 return (i+1); 41 } 42 void quick_sort(int* datas,int beg,int last) 43 { 44 int pivot; 45 if(beg < last) 46 { 47 pivot = partition(datas,beg,last); 48 quick_sort(datas,beg,pivot-1); 49 quick_sort(datas,pivot+1,last); 50 } 51 52 }
程序测试结果如下:

可以将划分过程之间嵌入到快速排序过程中,C语言实现如下所示:
1 void quicksort(int *datas,int length) 2 { 3 int pivot ,i,j; 4 if(length > 1) 5 { 6 pivot = datas[length-1]; 7 for(i=0,j=0;j<length-1;j++) 8 { 9 if(datas[j] < pivot) 10 { 11 swap(datas+i,datas+j); 12 i = i+1; 13 } 14 } 15 swap(datas+i,datas+length-1); 16 quicksort(datas,i); 17 quicksort(datas+i,length-i); 18 } 19 }
2、快速算法排序的性能
最快情况划分:当划分过程中产生的两个区域分别包含n-1个元素和1个元素的时候(即将待排序的数是逆序的),这样第个调用过程中每次划分都是不对称的。算法时间递归的表示为:T(n)=T(n-1)+T(o)+θ(n) = T(n-1)+θ(n) = θ(n^2)。例如下面的情况: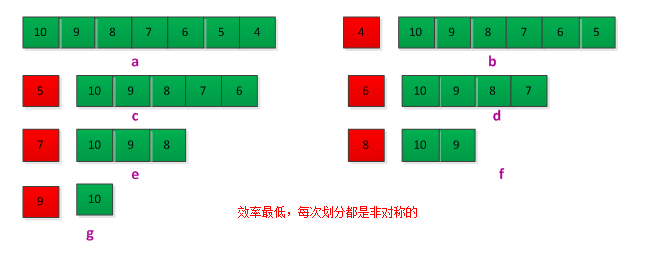
最佳情况划分:每次划分达到两个子问题的大小不可能都打大于n/2,当划分后一个两个子问题的大小分别为n/2(下取整)和n/2(上取整数)-1时候,快速排序时间最佳,这时候运行时间递归式为:T(n)<=2 T(n/2)+θ(n) = O(nlgn)。例如下面的情况: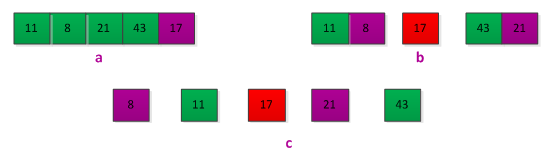
3、快速排序的随机化版本
前面快速排序在划分的时候总是以最后一个元素作为主元进行划分的,此时可以改用随机获取一个主元素,获得较好的评价功能。可以调用随机函数获取随机的主元素,然后进行划分。书中给出了为代码如下:
1 RANDOMIZED-PARTITION(A,p,r) 2 i = RANDOM(p,r) 3 exchange A[r] <->A[j] 4 return PARTITION(A,p,r)
