组合数学的基本原理
鸽巢原理(抽屉原理)
把 n+1 件东西放入 n 个抽屉,则至少有一个抽屉放了两件或两件以上的东西。从另一个角度说,把 n-1 个东西放入 n 个抽屉,则至少有一个抽屉是空的。
证明可以使用反证法。
第一抽屉原理
原理1 把多于 n+1 个物体放到 n 个抽屉里,则至少有一个抽屉里的物品不少于两件。
原理2 把多于 mn+1 个物体放在 n 个抽屉里,则至少有一个抽屉里有不少于 m+1 个物品。
原理3 把无穷多个物体放入 n 个抽屉,则至少有一个抽屉里有无穷个物体。
原理 1/2/3 都是对第一抽屉原理的表述。
第二抽屉原理
把 nm-1 个物体放入 n 个抽屉中,则其中必有一个抽屉中至多有 m-1 个物体。
构造抽屉的方法
有 12 个属相,任意 37 个人中,至少有多少人属相相同?将属相看成 12 个抽屉,则一个抽屉有 (lceil {frac{37}{12}} ceil = 4)
因此,在问题中,较多的一方就是物件,较少的一方就是抽屉。
最差原则
最差原则,即考虑所有可能的情况中,最不利于某件事情发生的情况。
例如,有 300 个人到招聘会求职,其中软件设计有 100 人,市场营销有 80 人,财务管理有 70 人,人力资源管理有 50 人。那么至少录取多少人才能保证一定有 70 人找的工作专业相同呢?此时考虑最差情况,软件设计、市场营销和财务管理各录取 69 人,人力资源管理的 50 人全部录取,则此时再录取 1 人就能保证有 70 人找到的专业相同。因此至少需要 (69 * 3 + 50 + 1 = 258) 人。
例题
例 1
已知 n+1 个正整数,它们全都小于或等于 2n,证明当中一定有两个数是互质的。
根据抽屉原理,n+1 个数中必定有两个数是连续的,即一定有两个数是互质的。
例 2
在一个边长为 2 厘米的等边三角形内(包括边界)选出 5 个点,请证明,一定有两个点之间的距离不大于 1
将这个边长为 2 厘米的等边三角形分成 4 个边长为 1 厘米的等边三角形,如图所示:

5 个点放在 4 个小三角形里,则至少有一个小三角形内放了两个点,同抽屉的两个点的距离不大于 1
例 3
在一个 7 * 7 的方格中,每个方格内都有一条小虫,约定在同一时刻内小虫必须向周围(上下左右四个格)爬一步。现在请证明:爬了一格后,至少有一个小方格是空的。
用“着色法”解决。如图所示:

25 个黑格,24 个白格,小虫只能从白格爬到黑格或从黑格爬到白格。一时刻后,24 个白格的小虫爬到 25 个黑格中,则至少有一个黑格是空格。
容斥原理
例题:
有 14 个同学学数学竞赛,20 个同学学信息竞赛,14 个同学学化学竞赛,4 个同时学数学和信息,3 个同时学数学和化学,2 个同时学信息和化学,1 个三者都学。问一共有几个学竞赛的同学?
维恩图表示方式:
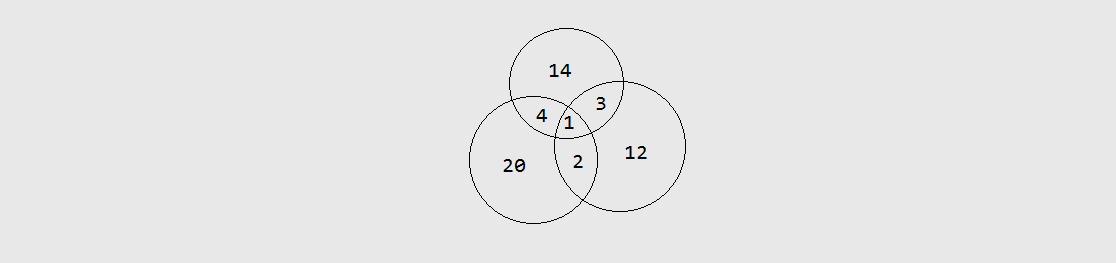
答案是 (14 + 20 + 12 - 4 - 3 - 2 + 1 = 38).
由上例可以看出,容斥原理的基本模式为“奇数加,偶数减”。
加法原理和乘法原理
因为定义比较简单,不展开做描述。
加法原理 分类独立完成,分类计数。
乘法原理 分步依次完成,分步计数。
四个不同的小球放入编号为 1,2,3,4 的四个盒子中,则恰好有一个空盒子的放法有多少种?从 4 个球中取出 2 个作为一组,与另两个球一起放入四个盒子中的三个内,有 (C_4^2 * A_4^3 = 144) 种放法。或将四个球分别放入 4 个盒子后,取出其中的两个盒子合并为一个盒子,有 (A_4^4 * C_4^2 = 144) 种放法。
排列
n 个不同元素中,任取 m 个元素,按照一定顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列。(与顺序有关)
排列数公式
(A_{n}^{m} = n(n-1)(n-2) ... (n-m+1) = frac{n!}{(n-m)!})(线排列公式)
当 n = m 时,有 (A_{n}^n = n!),即 n 的全排列;而把 0<m<n 的情况称为选排列。
圆排列
定义: 从集合 (S = { a_1, a_2, a_3,...a_n }) 的 n 个不同元素中,取出 (r) 个元素按照某种次序(如逆时针)排成一个圆圈,称这样的排列为圆排列。如果一个圆排列通过旋转可以得到另一个圆排列,则这两个圆排列是相同的。
一个圆排列可以产生 r 个线排列,而总共有 (A_n^r) 个线排列,因此圆排列的个数为 (frac{A_n^r}{r}=frac{n!}{r(n-r)!})
例题:
题目描述: 有 8 个人围圆桌就餐,问有多少种就坐方式?如果有两人不愿坐在一起,又有多少种就坐方式?
解: n=8, r=8,因此 8 人围圆桌就坐方式有 (frac{A_8^8}{8} = frac{8!}{8} = 7!) 种
设不愿坐在一起的两人为甲和乙,不妨考虑甲乙坐在一起的情况。此时,相当于 7 人围桌而坐,其就坐方式为 (frac{7!}{7}) (n=7, r=7)。而甲乙坐在一起又有两种情况,这样,甲和乙坐在一起时一共有 (2*6!) 种就坐方式。因此,甲和乙不坐在一起的就坐方式一共有 (7! - 2 * 6! = 3600) 种。
重排列
考虑在原先基础上允许重复出现的情况,即考虑在重集 $S = $ { (k_1 * a_1, k_2 * a_2, ..., k_n * a_n) } 中选 r 个元素进行排列。根据重复数 (k_1, k_2, ..., k_n) 是否趋向于 (infty),重排列又可以分为无限排列和有限排列。
无限重排列
例如,把 3 个不同的球放入 10 个不同的盒子中,若每个盒子能容纳的球只数无限,那么,蓝球和白球也能像红球一样放入 10 个盒子中的任意一个,所以放置的总方案数是 (10 * 10 * 10 = 10 ^ 3 = 1000) 种。
一般地,从 (n) 个元素中取 (r) 个按次序排列,若每个元素无限次重复(即 (k_1 = k_2 = k_3 = ... = k_n = infty)),则称排列为无限次排列,其排列数等于 (n^r)。
有限重排列
重集 $S = $ { (k_1 * a_1, k_2 * a_2, ..., k_n * a_n) } 中选 r 个元素进行排列,其中 (k_i eq infty)。
例如,有 2 个红球,1 个蓝球和 1 个白球,放到编号不同的 10 个盒子中,且每个盒子只能装 (1) 只球,有多少种放法?将两只红球分别涂成深红色和浅红色使之能区分,因此问题转化为 4 只不同颜色的球放入 10 个盒子中的方案数:(A_{10}^4 = 5040) 。在这 5040 种放法中,若不区分红球的深浅,那么两种方法变为一种方法,因此总方案数为 (frac{5040}{2} = 2520)。
错位排列
设 { (a_1, a_2, a_3, ...a_n) } 是 { (1, 2, ..., n) } 的一个全排列,对于 (i in) { (1, 2, ..., n) },都有 (a_i eq i),则称 { (a_1, a_2, ..., a_n) } 是 { (1, 2, ..., n) } 的一个错位排列。一般用 (D_n) 表示 { (1, 2, ..., n) } 的错位排列的个数。
通项公式:
(D_n = n! * (1 - frac{1}{1!} + frac{1}{2!} - frac{1}{3!} + frac{1}{4!} - ... + frac{(-1)^n}{n!}))
考虑从 n 个数里面选出 m 个数,这 m 个数都在自己的位置上的情况数。则首先从 n 个数里面取出 m 个,剩下的数随便放,即为:(C_n^m * (n-m)! = frac{n!}{m!(n-m)!}(n-m)! = frac{n!}{m!})。所有情况数 - 不合法情况数 = 合法情况数,根据容斥原理得到上式。
递推式:
设 (D_i) 表示 i 个数错排的情况数。若当前第 i 个位置放入了第 i 个数,分为下面两种情况
-
前 i-1 个数已经错排,i 与前面任意一个交换位置:((i-1)D_{i-1})
-
前 i-2 个数错排,i 与其中不合法的一个交换位置:((i-1)D_{i-2})
综上,错排问题的递推式为 (D_i = (i-1)(D_{i-1}+D_{i-2}))。
组合
从 (n) 个不同元素中,任取 m 个元素,并成一组,叫做从 n 个不同元素中取出 m 个元素的一个组合。(与顺序无关)
组合数公式: (C_{n}^m = frac{A_{n}^m}{A_{m}^m} = frac{n!}{m!(n-m)!})
组合数的性质
性质 1:
(C_{n}^m = C_{n}^{n-m})
可以理解为:从 n 个数中选出 m 个数 = 从 n 个数中扔掉 n-m 个数的
性质 2:
(C_{n}^r = C_{n-1}^r + C_{n-1}^{r-1})
证明: 利用动态规划证明。设 (f_{i,j}) 表示已经在 i 个元素中抽取了 j 个元素:1.这一步没有抽取元素:(f_{i,j} = f_{i-1,j});2.这一步抽取了一个元素:(f_{i,j} = f_{i-1,j-1})。综上,(f_{i,j} = f_{i-1,j} + f_{i-1,j-1}),等同于杨辉三角形公式。
性质 3:
(C_n^0 + c_n^1 + C_n^2... + C_n^{n-1} + C_n^n = 2^n)
杨辉三角形用在 ((x+y)^n) 的展开系数上称为二项式定理。
暂未找到证明 QwQ
可重复组合
在计算、生成组合时可以允许元素重复的一类组合问题。例如,对于有四个元素的集合 { a, b, c, d },其可重复组合 (H_4^3 = 20),其中包含 aaa/bdd 等。
公式: (H_n^r = C_{n+r-1}^r)
理解: 可以把问题带入生活中:有 5 种冰激凌口味:香蕉、巧克力、柠檬、草莓和香草,我想要三球。一些选择:{ c, c, c }, { b, l, v }, { b, v, v }。想象冰激凌在 5 个筒里(依次为 b/c/l/s/v),命令一个机器人挖冰激凌,O 表示挖,> 表示移动。上面三个例子就是这样的:

到此,问题转化成了从(7)个数中选出(4)个箭头、(3)个球的排列方式。等同于以上公式。
二项式定理: ((a+b)^n=Sigma_{k=0}^{n}C_n^ka_{n-k}b^k)
课后习题
NOIP2011 计算系数
因为新开一个随笔写这个没啥意思,就直接放在这里吧...
Solution
裸的组合数(二项式定理)。原数列的 (x^ny^m) 项对应的系数是 (C_{n+m}^m),这个数最后 (*a^n*b^m) 得到答案。于是可以预处理组合数求解。
Code
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const long long mod = 10007;
long long a, b, k, n, m, c[2333][2333], a1[2333], a2[2333];
int main()
{
scanf("%d%d%d%d%d", &a, &b, &k, &n, &m);
memset(c, 0, sizeof(c));
a1[0] = a2[0] = 1;
for(int i = 1; i <= 2000; i++) a1[i] = (a1[i - 1] * a) % mod;
for(int i = 1; i <= 2000; i++) a2[i] = (a2[i - 1] * b) % mod;
c[1][1] = 1;
for(int i = 1; i <= 2000; i++) c[i][0] = 1;
for(int i = 2; i <= 2000; i++)
for(int j = 1; j <= i; j++)
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
printf("%d", (c[k][m] * a1[n] * a2[m]) % mod);
return 0;
}