长度最小的连续子数组
问题描述
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组,并返回其长度。如果不存在符合条件的连续子数组,返回 0。
示例:
输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
问题解决方案
暴力求解
首先这道题最明显能想到的就是暴力求解,两个for循环,第一个记录开始的索引,第二个记录当大于等于正整数s时的末尾索引,当得到的连续子数组的总和≥s且长度小于最小值时,更新最小值。
void function(int n, int s, int nums[]) {
int min = n + 1;
for (int i = 0; i < n; i++) {
int length = 1;
int sum = nums[i];
for (int j = i + 1; j < n; j++) {
length++;
if (sum + nums[j] >= s && min > length) {
min = length;
break;
} else {
sum += nums[j];
}
}
}
if (min == n + 1) {
cout << "min = 0" << endl;
} else {
cout << "min = " << min << endl;
}
}
显而易见,时间复杂度在O(n^2)量级上;
使用队列
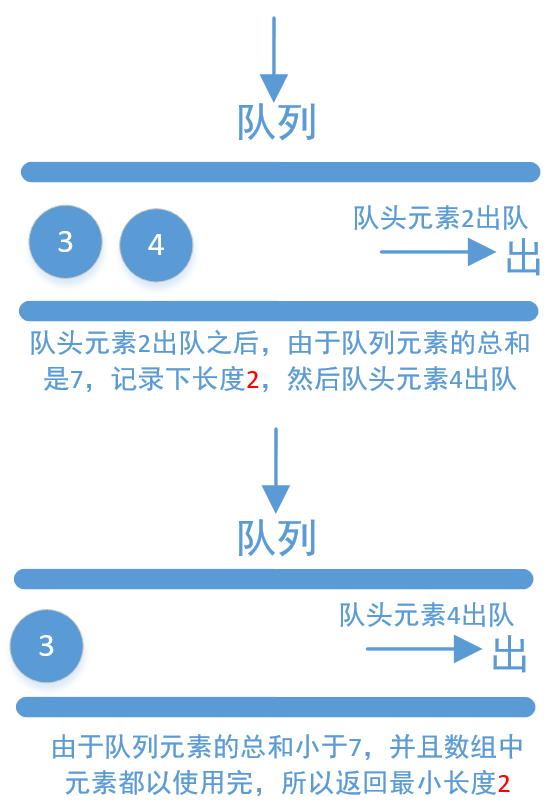
该方法定义两个指针,首指针和尾指针,也可以看作是数组的下标索引(high表示尾指针,对应大的下标索引值;low表示首指针,对应小的索引值。nums[low]~nums[high])。解决的原则是一开始默认为0,当sum(子数组的总和)小于s时,high向后移动一位(high++)。当sum大于等于s时,判断当前的长度,如果长度小于最小值,更新最小值,然后low向后移动一位(low++)。直到high跑出数组外,也就是(high>=n)
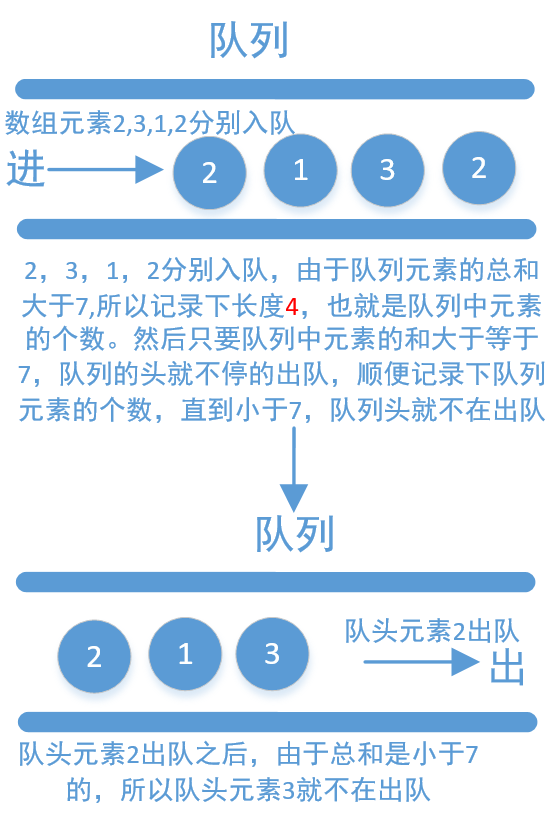
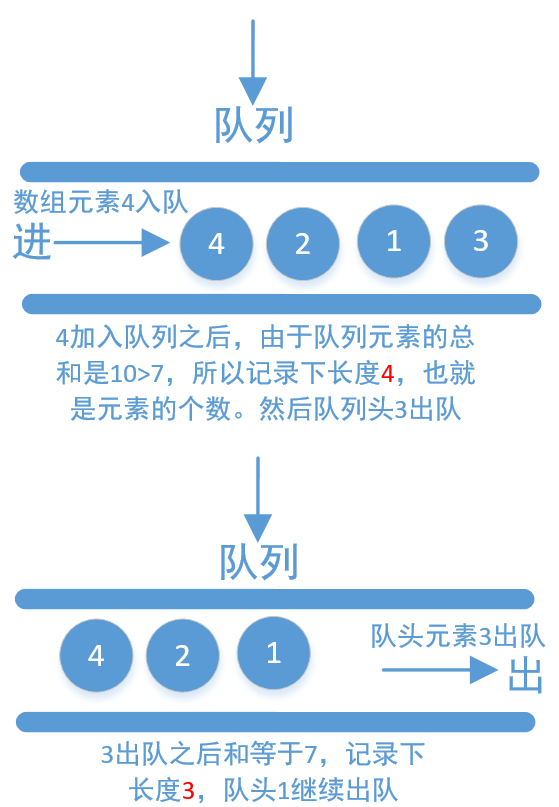
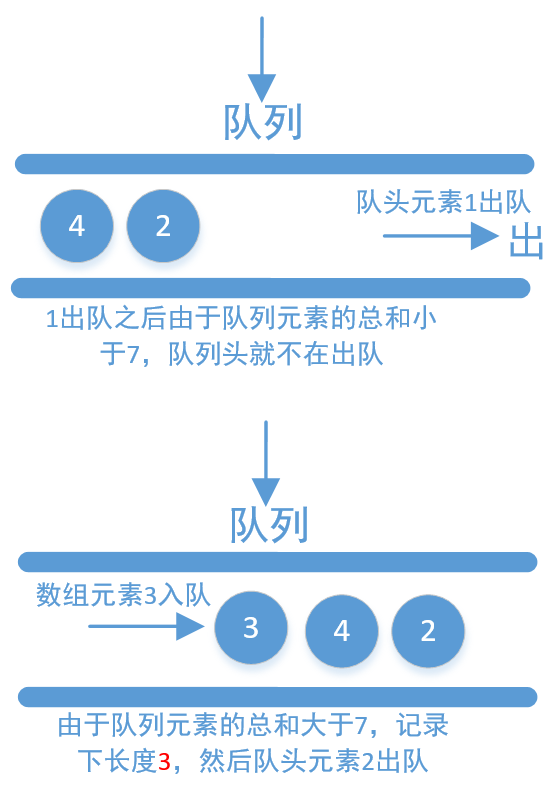
void function2(int s, int n, int nums[]) {
int min = n + 1;
int high = 0, low = 0, sum = 0;
while (high < n) {
sum += nums[high++];
while (sum >= s) {
if (high - low < min)
min = high - low;
sum -= nums[low++];
}
}
cout << "min = " << min << endl;
}
时间复杂度为O(2*n)
完整代码:
void function(int n, int s, int nums[]) {
int min = n + 1;
for (int i = 0; i < n; i++) {
int length = 1;
int sum = nums[i];
for (int j = i + 1; j < n; j++) {
length++;
if (sum + nums[j] >= s && min > length) {
min = length;
break;
} else {
sum += nums[j];
}
}
}
if (min == n + 1) {
cout << "min = 0" << endl;
} else {
cout << "min = " << min << endl;
}
}
void function2(int s, int n, int nums[]) {
int min = n + 1;
int high = 0, low = 0, sum = 0;
while (high < n) {
sum += nums[high++];
while (sum >= s) {
if (high - low < min)
min = high - low;
sum -= nums[low++];
}
}
cout << "min = " << min << endl;
}
void function3(int s,int n,int nums[]){
int min = n+1;
int high=0, low =0,sum = 0;
while(high < n){
s-=nums[high++];
while(s<=0){
if(min > high - low){
min = high -low;
}
s+=nums[low++];
}
}
cout << "min = " << min << endl;
}
int main() {
int n, s;
cin >> n >> s;
int nums[n];
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
function(s,n,nums);
function2(s,n,nums);
}