[题解] poj 3159 Candies (dijkstra最短路+差分约束)

- 传送门 -

　http://poj.org/problem?id=3159

#Candies | **Time Limit:** 1500MS |   | **Memory Limit:** 131072K | | **Total Submissions:** 33044 |   | **Accepted:** 9265 |

Description

During the kindergarten days, flymouse was the monitor of his class. Occasionally the head-teacher brought the kids of flymouse’s class a large bag of candies and had flymouse distribute them. All the kids loved candies very much and often compared the numbers of candies they got with others. A kid A could had the idea that though it might be the case that another kid B was better than him in some aspect and therefore had a reason for deserving more candies than he did, he should never get a certain number of candies fewer than B did no matter how many candies he actually got, otherwise he would feel dissatisfied and go to the head-teacher to complain about flymouse’s biased distribution.

snoopy shared class with flymouse at that time. flymouse always compared the number of his candies with that of snoopy’s. He wanted to make the difference between the numbers as large as possible while keeping every kid satisfied. Now he had just got another bag of candies from the head-teacher, what was the largest difference he could make out of it?

Input

The input contains a single test cases. The test cases starts with a line with two integers N and M not exceeding 30 000 and 150 000 respectively. N is the number of kids in the class and the kids were numbered 1 through N. snoopy and flymouse were always numbered 1 and N. Then follow _M_lines each holding three integers A, B and c in order, meaning that kid A believed that kid B should never get over c candies more than he did.

Output

Output one line with only the largest difference desired. The difference is guaranteed to be finite.

Sample Input

2 2
1 2 5
2 1 4

Sample Output

5

[Submit]   [Status]   [Discuss]

- 题意 -

　对n个小朋友分糖果并满足m个条件.
　条件格式如下:
　A B C
　表示B比A多的糖果不能超过C.
　求n号比1号小朋友多出糖果的最大值.
　

- 思路 -

　从 A 向 B 连一条权值为 C 的边, 求最短路.
　
　关键是这个模型是怎么转化得来的?
　这是详解: http://www.cppblog.com/menjitianya/archive/2015/11/19/212292.html
　这是我的思考: http://www.cnblogs.com/Anding-16/p/7399855.html
　
　设给出的数据为:
　A B V2 ---(1)
　A C V1 ---(2)
　B C V3 ---(3)
　由数据可以看出:
　((2):C leq A+V1)
　((1)(3): A+V2geq B, B+V3geq C)
　即(Cleq A+V2+V3)
　所以在A默认取 0 时, (C_{max} = min(V1, V2 + V3))
　
　如图:

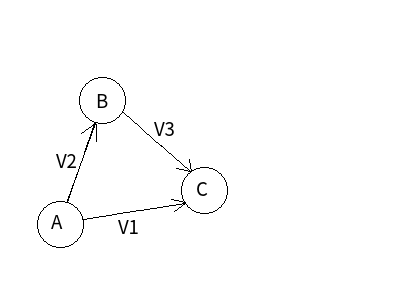
　画出这样一个有向图, 可以看出:
　对于(A o C)这条路, 它表示:
　　(DIS[A]+V1=DIS[C]);
　对于(A o B o C)这条路, 它表示:
　　(DIS[A]+V2=DIS[B],DIS[B]+V3=DIS[C])
　　即(DIS[A]+V2+V3=DIS[C])
　(DIS[A] = 0), 故(DIS[C]=min(V1,V2+V3))
　
　发现(DIS[C] = C_{max}), 说明这种情况下最短路就是解, 其它情况也都是这样子, 就意会一下好了~
　想要详细证明的话还是看上面的链接好了.
　
　细节见代码.
　

- 代码 -

#include<cstdio>
#include<queue>
#include<algorithm>
#include<cstring>
#define ft first
#define sd second
using namespace std;

typedef pair<int, int> pii;
const int N = 3e4 + 5;
const int M = 150000 + 5;

int DIS[N], VIS[N];
int V[M], NXT[M], TO[M], HD[N];
int n, m, x, y, v, sz;
priority_queue<pii,vector<pii>,greater<pii> >Q;

void add(int x, int y, int v) {
	V[++sz] = v; TO[sz] = y; NXT[sz] = HD[x]; HD[x] = sz;
}

void init() {
	memset(VIS, 0, sizeof (VIS));
	memset(DIS, 0x3f, sizeof (DIS));
	DIS[1] = 0;
}

void dijkstra() {
	pii st = make_pair(0, 1);
	Q.push(st);
	while (!Q.empty()) {
		pii x = Q.top();
		Q.pop();
		int u = x.sd;
		VIS[u] = 1;
		for (int i = HD[u]; i; i = NXT[i]) {
			int v = TO[i];
			if (!VIS[v] && DIS[v] > DIS[u] + V[i]) {
				DIS[v] = DIS[u] + V[i];
				pii y = make_pair(DIS[v], v);
				Q.push(y);
			}
		}
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; ++i) {
		scanf("%d%d%d", &x, &y, &v);
		add(x, y, v);
	}
	init();
	dijkstra();
	printf("%d
", DIS[n]);
	return 0;
}