###过拟合问题
Overfitting problem 过拟合问题
Regularization 正则化
Ameliorate 改善
Underfitting 欠拟合 high bias 高偏差
Preconception 偏见
Quadratic function二阶项
Extreme 极端
Wiggly波动

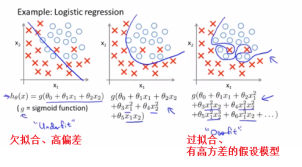
If we’re fitting such a high order polynomial,then the hypothesis can fit,it’s almost as if it can fit almost any function.And this face of possible hypothesis is just too large,it’s too variable.And we don’t have enough data to constrain it to give us a good hypothesis,so that’s called overfitting.
如果我们拟合一个高阶多项式,那么这个假设函数,能拟合几乎所有的数据。这就面临可能的函数太过于庞大,变量太多的问题。并且我们没有足够的数据来约束它来获得一个好的假设函数,这就是过度拟合。

Constrain 约束
High order polynomial 高阶多项式
Contort 扭曲
Debug 调试
Diagnose 诊断

If we have a lot of features and very little training data,then overfitting can become a problem.
如果我们有过多的变量,但是只有非常少的训练数据,就会出现过度拟合的问题。
Manually人工地
Throw out 舍弃
Model selection 模型选择
Magnitude 量级
###代价函数
Convey to you向你们介绍
Generalize 泛化
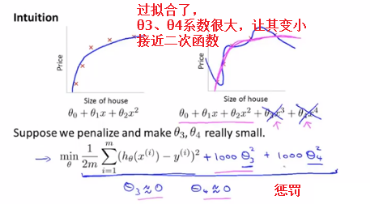
我们对θ_3和θ_4加入了惩罚项
Small terms特别小的项
The ideal is that ,if we have small values for the parameters,then having small values for the parameters will somehow,will usually correspond to having a simpler hypothesis
正则化的思想就是,如果我们的参数值较小,参数值较小就意味着一个更简单的假设模型。
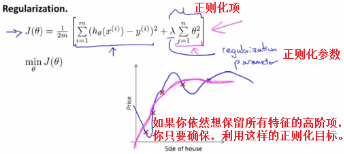
Writing down our regularized optimization objective,our regularized cost function again.Here it is.
写下正则化的优化目标,也就是正则化代价函数,也就是J(θ)
The λ is controls a trade off between two different goals.The first goal,captured by the first term of the objective,is that we would like to train,is that we would like to fit the training data well,we would like to fit the training set well.And the second goal is,we want to keep the parameters small.the lambda is the regularization parameter does,is the controls the trade off between these two goals.
Λ控制着两个不同目标之间的取舍。第一个目标,和目标函数的第一项有关,就是我们想去训练,想要更好地拟合数据,更好的拟合训练集。而第二个目标就是,我们想要保持参数尽量地小。Λ也就是正则化参数,作用是控制这两个目标之间的平衡关系。
Smooth平滑

So for sure regularization to work well,some care should be taken,to choose a good choice for the good regularization parameter lambda as well.
为了让正则化起到应有的效果,我们应该注意一下,去选择一个更合适的正则化参数λ
###线性回归的正则化
【目前为止,我学了线性回归,logistic回归,正则化】
【线性回归中,推导过两种办法1梯度下降 2正则方程】

然后找一个参数θ,来最小化代价函数J(θ)。

在没有正则化的梯度下降法中,我们不断的更新θ,当j从0到n。
