Matrices、matrix 矩阵 vectors 向量
array 排列
Element 元素
A matrix is a rectangular array of numbers,written between square brackets
矩阵是由数字组成的矩形阵列,并写在方括号内
Square bracket 方括号
a bunch of 一堆
Row 行 column 列
Matrix is just another way for saying ,2D or two dimensional array
矩阵可以说是二维数组的另一种说法
Over除以
One over zero is not well defined 1除以0是无意义的
Times、multiplied by.乘以
Three times two is six 3x2=6
A m by m matrix 一个m x m的矩阵
Dimension of matrix :number of rows x number of columns
矩阵的维度:行数x列数
Matrices of a specific dimension 一个特定维度的矩阵

The dimension of this matrix is 2 by 3
(这个矩阵的维数是2x3)
Standard notation 标准符号 notation 符号
Entry 条目
A12 is going to refer to the entry in the first row and the second column
(A12表达的是第一行第二列对应的项)
Matrices let you quickly organize ,index and access lots of data.
(矩阵让你快速整理,索引和访问大量数据)
The lecture notes 课程讲义
Course website课程网页 audible lecture音频

a four dimensional vector 一个四维的向量
A vector turns out to be a special case of a matrix.A vector is a matrix that has only 1 column.
(一个向量是一种特殊的矩阵。向量是只有一列的矩阵。)
This R4,again just means a set of all four-dimensional vector
(这个R^4指一个四维向量的集合)
Y subscript i is the ith element.
(y_i是第i个元素)
Sequence序列
A more convenient notation 一个更方便的符号
By convention 按照惯例
Upper case 、Capital letter大写字母--matrix矩阵
Lower case小写字母--vector向量
Addition 加法 、 subtraction 减法、multiply 乘法、divide 除以
As well as 和
Scalar Multiplication 标量乘法
The same dimension 相同维度
You just add up the elements of these matrices one at a time.
(这两个矩阵的每一个元素都逐个相加)
A three by two matrix一个3x2的矩阵
A scalar number 标量--常量
Real number 实数
Divide it by a number除以一个数
One quarter 1/4
three halves 1/3
Plus 加
One matrix multiplication operation 一次矩阵的乘法运算
Commutative 可交换
commutative property of multiplication of real numbers 实数乘法的交换率
Reverse the order 颠倒顺序
Concretely 具体地
Arbitrarily 随意地
As a concrete example 举一个具体的例子
Swap 交换
The associative property of real number multiplication 数乘的结合律
Enjoy the associative property 服从结合律
Terminology 术语
矩阵没有交换律,但是有结合律。
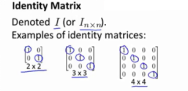
identity matrix ,which id special matrix 一种特殊的矩阵---单位矩阵
The identity matrix has the property that has ones along the diagonals ,and is zero everywhere else.
单位矩阵有一个特性,即对角线都是1,其他位置都是0
Sloppy 稀疏的 sloppily write随意的写
Diagonals 对角线
Implicit 暗含
Inverse 倒数
Matrix inverse and matrix transpose operation 矩阵的逆和转置运算
One third 1/3
Twelve to the minus one ---- one twelve 12的-1次方
Only matrices that are m by m for some value of m have an inverse.------a square matrix方阵
(只有m x m 的矩阵才有其逆矩阵only square matrices have inverses)
It satisfies this equation.它满足这个等式
A concrete example 一个具体的例子
Numerical software for taking a matrix and computing its inverse
(能很容易对矩阵进行求逆运算的数字软件)
Open source libraries 开源库
A quick example 一个简单的例子
Octave
Type 键入
Pinv of A---- pinv(A)
Verify 证实
Essentially 基本上
Up to取决于、考虑到
Numerical precision 计算精度
precision 、Precisely精确
Caveat 警告
Fix 处理
One intuition you might take away is that just as the number zero doesn’t have an inverse
(有一点你可以理解为,数字0没有倒数)
Matrices that don’t have an inverse are “singular” or “degenerate”
(没有逆的矩阵叫奇异矩阵、或者是退化矩阵--无限接近于0的)
Superscript 标---A superscript T----A矩阵的转置
45 degree axis 45度的轴
Mirror 镜子
Flip 翻转
Reverse 相反
Absorb 吸收
Linear algebra tools线性代数工具
Derive 推导
The more formal definition of a matrix transpose
(矩阵转置的更正式的定义)