概念
虚树,顾名思义就是虚构的树,它是一种用来解决树上问题的算法,主要思想是只将原树上必要的点和它们的最近公共祖先取出来,构成一棵虚树,并保留他们在树上的相对关系。
引入
我们先来看一道题:
给定一棵n个点的树,每次询问给定一个大小为k的点集,你需要切掉一些边,使得点集中的点均不与1号点联通,而每条边都有被切掉所需的代价,你还要让总代价最小。(2 leqslant n leqslant 250000,,sum ki leqslant 500000,1 leqslant k_i leqslant n-1)
(来源:Bzoj_2286 Sdoi2011消耗战)
对于单个询问,我们可以用Tree_Dp在O(n)的时间内得到答案,这样显然太慢。但是,我们发现实际上询问的总点集大小并不大,如果每次询问能不将整棵树都遍历而只遍历询问的点,那么复杂度就可以降下来了。因此我们需要用到虚树。
构建
构建虚树采取的思路是:将点“从左到右”地添加。
我们先要将树遍历一遍给每个点记一个dfs序,然后将询问点按dfs序排序。
用栈维护一条当前虚树内“最靠右”的一条链,按顺序加点。
假设当前准备加入的点为x,如果当前栈顶不是x的祖先,则弹栈,并向上一个弹出的点(仅在本轮操作中)连边,直到是或栈为空为止,顺便记录弹出的点与点x的最近公共祖先LCA(弹出的所有点与点x的最近公共祖先一定相同)。
将LCA与最后一个弹栈的点连边,之后再判断LCA是否已在栈顶,否则入栈。点x入栈。这样栈中一定是“最靠右”的链。
复杂度(O(klogn))
以下图为例,绿色点表示询问点,蓝色点表示进入虚树的点,红色点表示栈里的点。
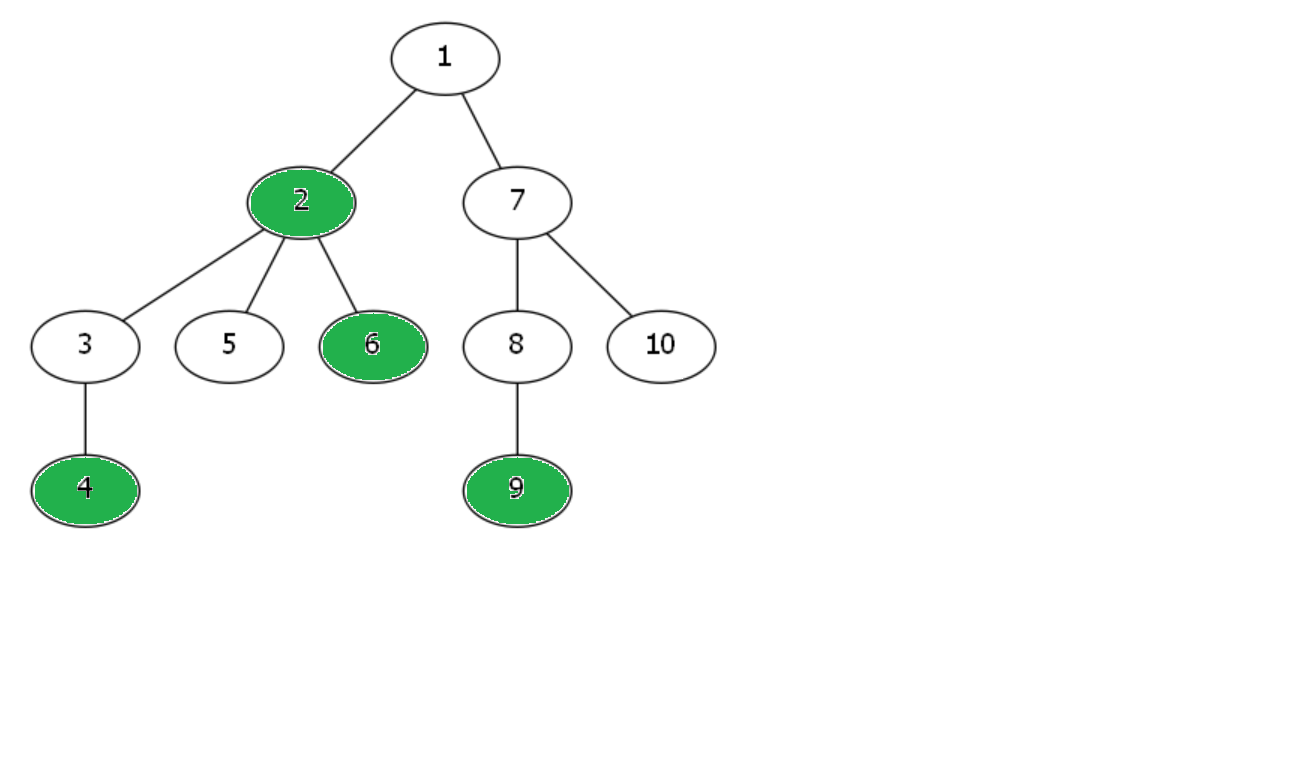
加入2号点:
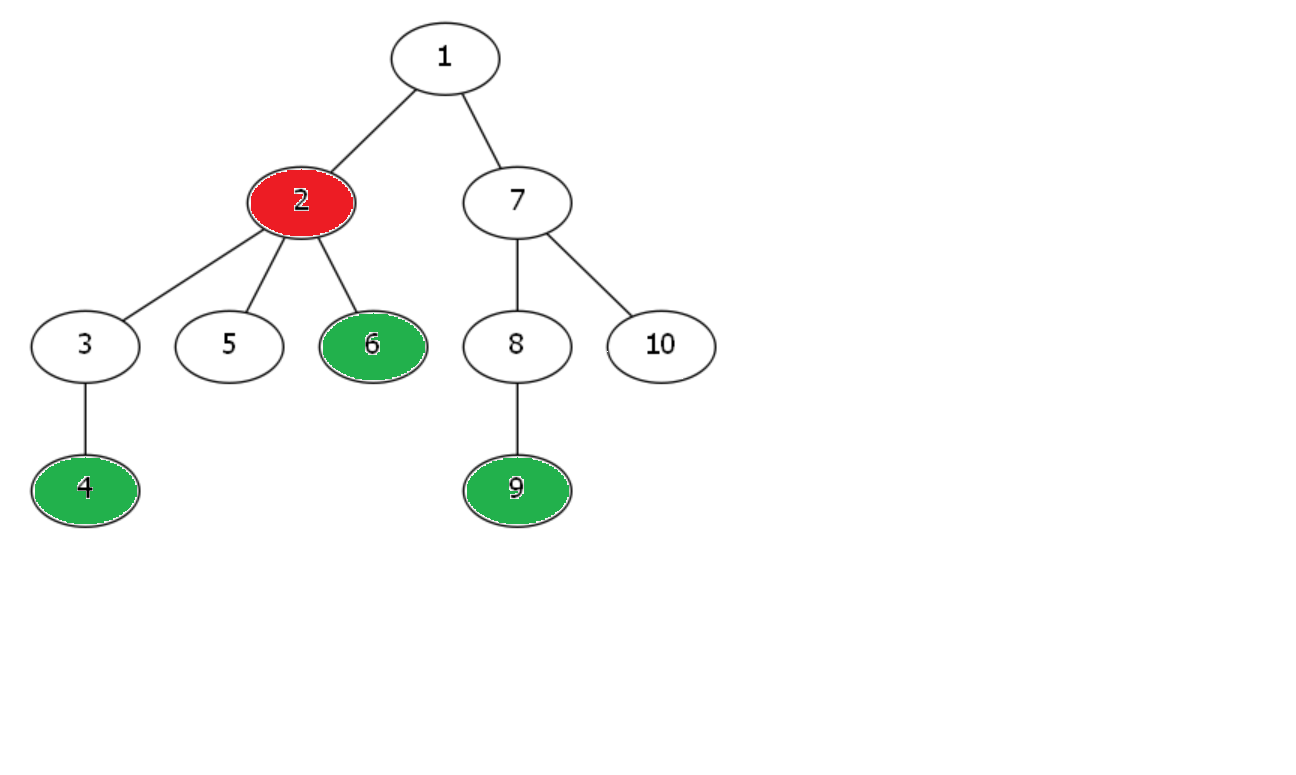
加入4号点:
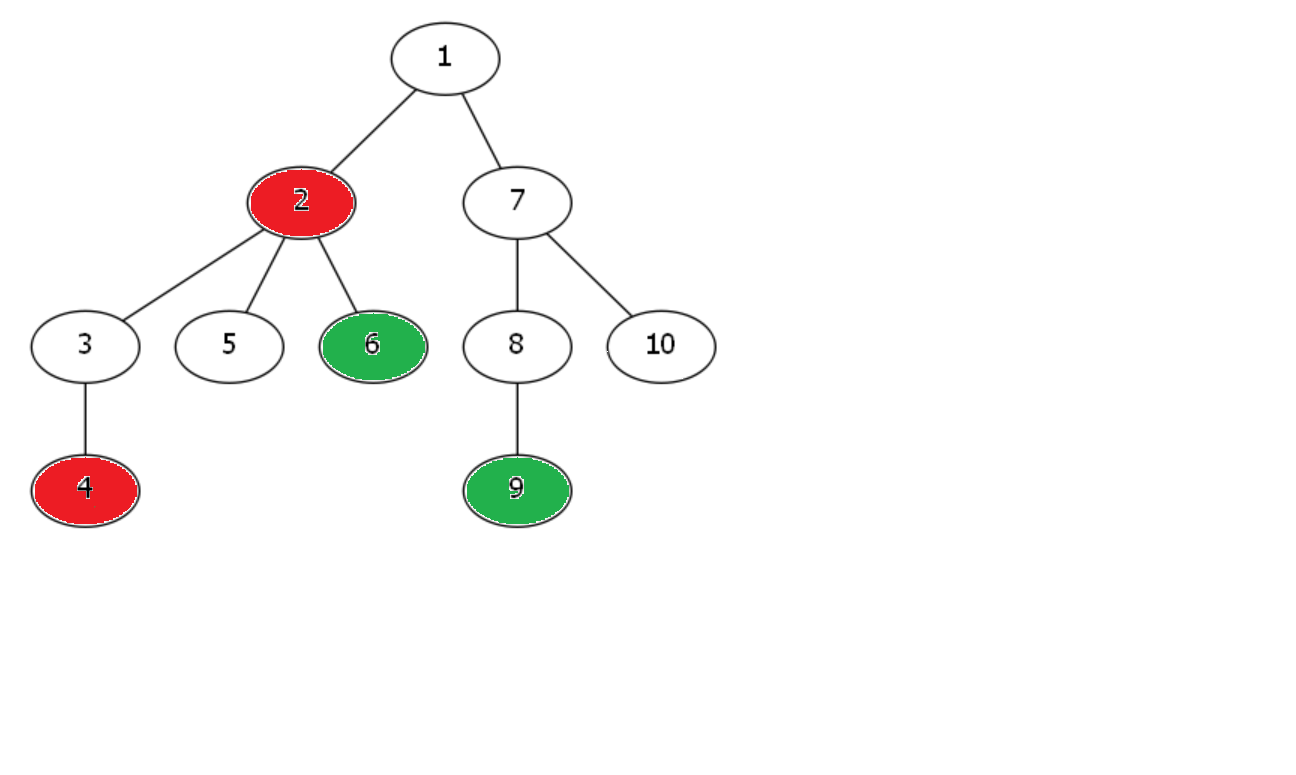
加入6号点,2和4连边:
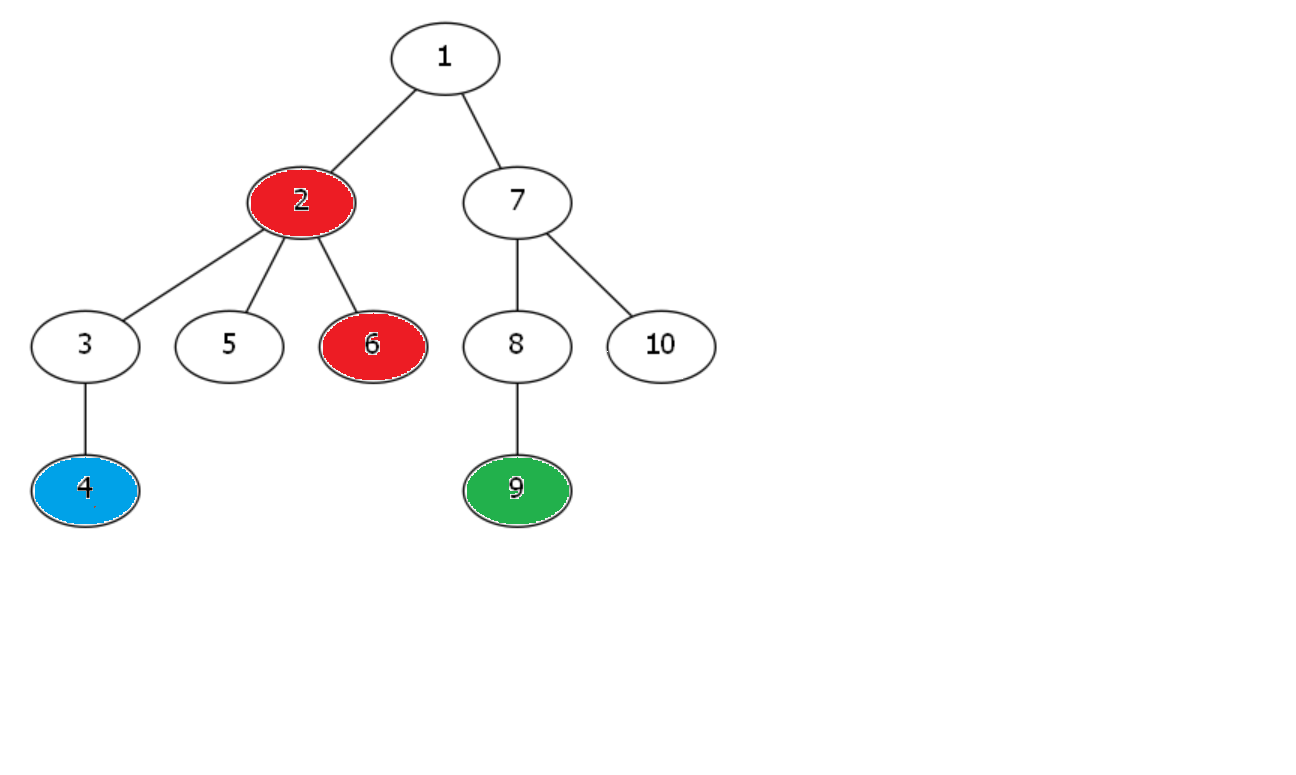
加入9号点,2和6连边、1和2连边:
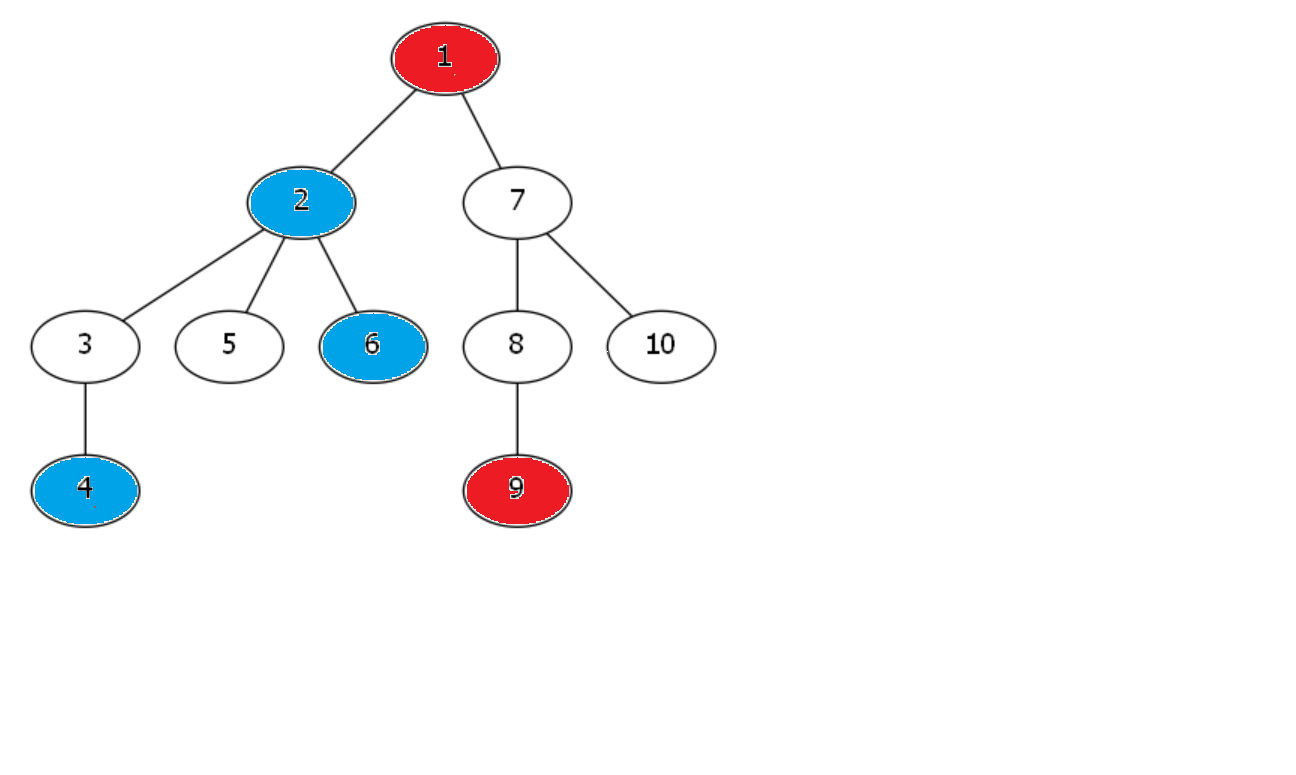
最后再将栈内的1和9连边。
解决
那么我们回到原题,现在知道如何建虚树了,如果解决问题?
首先我们要有一个小技巧,就是对于一个询问点,如果某个询问点是它的祖先,那么就可以把它从询问点中删除。这样询问点之间就没有祖先关系了。我们还需要为每个点记一个值,为它到根(1号点)的路径中最小代价的边,记为(v_x)。
那么建出虚树后,我们对于虚树中的叶子节点x,其dp值为(v_x)。对于非叶子节点x,dp值为(min(v_x,sum dp_{son})),son为它的直系儿子,1号点的dp值即为最终答案。
后续
提供一个建虚树的板子

这里还有些用到虚树的题,可供参考。
Bzoj 3991 SDOI2015寻宝游戏
Bzoj 3611 Heoi2014大工程
Bzoj 3572 Hnoi2014世界树
Luogu_4242 树上的毒瘤
Bzoj 5287 Hnoi2018毒瘤