2018/8/17 农历 七月初七
今天这个特殊的日子,不知道各位算友都过得怎么样~
适逢七夕,写算法题当然是众汪所归啊!所以今天,我们带来了一道以七夕为背景的题目。
题目:七夕祭(BZOJ3032有权限,可在JoyOI和CodeVS上查找提交)
题目背景:
七夕节因牛郎织女的传说而被扣上了「情人节」的帽子。于是TYVJ今年举办了一次线下七夕祭。Vani同学今年成功邀请到了cl同学陪他来共度七夕,于是他们决定去TYVJ七夕祭游玩。
题目描述:
TYVJ七夕祭和11区的夏祭的形式很像。矩形的祭典会场由N排M列共计N×M个摊点组成。虽然摊点种类繁多,不过cl只对其中的一部分摊点感兴趣,比如章鱼烧、苹果糖、棉花糖、射的屋……什么的。Vani预先联系了七夕祭的负责人zhq,希望能够通过恰当地布置会场,使得各行中cl感兴趣的摊点数一样多,并且各列中cl感兴趣的摊点数也一样多。
不过zhq告诉Vani,摊点已经随意布置完毕了,如果想满足cl的要求,唯一的调整方式就是交换两个相邻的摊点。两个摊点相邻,当且仅当他们处在同一行或者同一列的相邻位置上。由于zhq率领的TYVJ开发小组成功地扭曲了空间,每一行或每一列的第一个位置和最后一个位置也算作相邻。现在Vani想知道他的两个要求最多能满足多少个。在此前提下,至少需要交换多少次摊点。
输入格式:
第一行包含三个整数N和M和T。T表示cl对多少个摊点感兴趣。
接下来T行,每行两个整数x, y,表示cl对处在第x行第y列的摊点感兴趣。
输出格式:
首先输出一个字符串。如果能满足Vani的全部两个要求,输出both;如果通过调整只能使得各行中cl感兴趣的摊点数一样多,输出row;如果只能使各列中cl感兴趣的摊点数一样多,输出column;如果均不能满足,输出impossible。
如果输出的字符串不是impossible, 接下来输出最小交换次数,与字符串之间用一个空格隔开。
提示:
对于30% 的数据,N, M≤100。
对于70% 的数据,N, M≤1000。
对于100% 的数据,1≤N, M≤100000,0≤T≤min(NM, 100000),1≤x≤N,1≤y≤M。
输入样例:
样例输入1
2 3 4
1 3
2 1
2 2
2 3
样例输入2
3 3 3
1 3
2 2
2 3
输出样例:
样例输出1
row 1
样例输出2
both 2
提示:环形均分纸牌、中位数的性质。
思路:
首先我们只要想一想就会发现只要用 t 去模 n和m 就能根据是否整除得到字符串输出是哪个。而且整除的结果就是最后移动后的均摊结果。
然后就可以发现这是个横向和纵向的均分纸牌有木有?(均分纸牌是noip2002的一道经典贪心题目,并不难,希望掌握以后再往下看……不懂记得问)
不加证明地给出行和列分别求就可以了不会影响,因为这一行的点互相交换并不会影响这一列的点的个数。
那我们以行为例:
在均分纸牌中,我们会用a[i] = c[i](实际上这行的数量)-average(均分后的结果)来便于操作,所以a[i]可能是正的也可能是负的,a[i]==0就说明这一行已经达成目标。
而 abs(a[i]) 就是要对这一行进行的操作数,通过前缀和s[i] = a[i] + s[i-1],我们可以通过 ∑mi=1 | s[i] | (m是行数)得到最后所需的总移动次数。
以上为均分纸牌的内容,并没有详细讲。接下来只剩下一个问题了,就是这并不是原来的均分纸牌,此题由于可以画环,所以并不能完全把前缀和 s[i] 加起来就解决了。
此处希望读者在脑中、纸上自行想象如果第一行和最后一行相接会出现怎样的、比常规更巧的分配方式。
然后当我们不知道怎么处理之时神来之笔就是:一定存在一种最优解的方案,环上某两个相邻的人之间没有发生纸牌交换操作。因此我们可以在这里把环断开,就当成从第k+1个人开始依次往下分,像原来一样均分纸牌,一直分到第k个人结束。
普通的均分纸牌是这样的:

我们从第k+1个开始的均分纸牌是这样的:

所以由于s[m]肯定是等于0的,我们所需结果从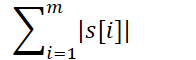 变成了
变成了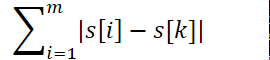
接下来的问题是如果遍历k的话复杂度撑不住。
巧求k,化公式为问题:坐标轴上有m个点,怎样取一个第k点,使得各点到此点的距离之和最短。
结论:1~m个点的坐标排序后的中位数第k个点即是所需点。
简略说明:假如k点左边现在有P个点,右边现在有Q个点,当k点在坐标轴上向右移动一个单位时,左边每个点都远离它一个单位,右边每个点都接近它一个单位,总距离比刚才减少了Q-P个单位;这个过程继续下去,当k为中位点是P=Q,没法再少了,再往右走就过分了,同理得往左走了。
所以回到问题,可以把 s[i] 排序后直接取中位点即可。
至此所有的问题都解决了,如果都理解了的话可以自己动手解决了,如还有没理解可以结合代码看看、搜搜资料、后台留言……最大复杂度(nlogn+mlogm)
1 #include <bits/stdc++.h> 2 #define maxn 100005 3 using namespace std; 4 5 int n, m, t, flag; 6 long long ans; 7 int rows[maxn], columns[maxn]; 8 9 void solve(int *a, int c) 10 { 11 int average = t / c; 12 int s[maxn] = {0}; 13 14 for (int i = 1; i <= c; i++) 15 a[i] -= average, s[i] = a[i] + s[i-1]; 16 sort (s+1, s+1+c); 17 for (int i = 1; i <= c; i++) 18 ans += abs(s[i] - s[(c+1)>>1]); 19 } 20 21 int main() 22 { 23 scanf("%d%d%d", &n, &m, &t); 24 for (int i = 0; i < t; ++i) 25 { 26 int x, y; 27 scanf("%d%d", &x, &y); 28 rows[x]++; 29 columns[y]++; 30 } 31 32 if (t % n == 0) 33 { 34 flag++; 35 solve(rows, n); 36 } 37 if (t % m == 0) 38 { 39 flag += 2; 40 solve(columns, m); 41 } 42 43 if (flag == 0) printf("impossible"); 44 else if (flag == 1) printf("row "); 45 else if (flag == 2) printf("column "); 46 else if (flag == 3) printf("both "); 47 48 if (flag) printf("%lld", ans); 49 }