Computer Vision_18_Image Stitching： Image Alignment and Stitching A Tutorial——2006（book）

此部分是计算机视觉部分，主要侧重在底层特征提取，视频分析，跟踪，目标检测和识别方面等方面。对于自己不太熟悉的领域比如摄像机标定和立体视觉，仅仅列出上google上引用次数比较多的文献。有一些刚刚出版的文章，个人非常喜欢，也列出来了。

18. Image Stitching
图像拼接，另一个相关的词是Panoramic。在Computer Vision: Algorithms and Applications一书中，有专门一章是讨论这个问题。这里的两面文章一篇是综述，一篇是这方面很经典的文章。
[2006 Fnd] Image Alignment and Stitching A Tutorial
[2007 IJCV] Automatic Panoramic Image Stitching using Invariant Features

若引用文献：Szeliski R . Image Alignment and Stitching: A Tutorial[J]. Foundations and Trends® in Computer Graphics and Vision, 2006, 2(1):1-104.

翻译

图像对齐和拼接教程——http://tongtianta.site/paper/57879

http://tongtianta.site/paper/57873

作者：Richard Szeliski

 http://www.research.microsoft.com

　　1该报告的简短版本出现在Paragios，N.等人，《计算机视觉的数学模型手册》，第273-292页，Springer，2005年的编辑中。

摘要 -本教程将介绍图像对齐和图像拼接算法。 图像对齐算法可以发现重叠程度不同的图像之间的对应关系。 它们非常适合视频稳定，摘要和全景马赛克的创建等应用。 图像拼接算法采用由此类配准算法产生的对齐估计，并以无缝方式混合图像，并小心处理诸如视差和场景移动以及变化的图像曝光等可能引起的模糊或重影等潜在问题。 本教程回顾了对齐和缝合算法基础的基本运动模型，描述了有效的直接(基于像素)和基于特征的对齐算法，并描述了用于产生无缝镶嵌的混合算法。 最后，讨论该地区的开放研究问题。

内容
1简介1
2运动模型2
2.1 2D(平面)运动3
2.2 3D转换5
2.3圆柱坐标和球坐标11
2.4镜头变形14
3直接(基于像素)对齐15
3.1错误指标16
3.2分层运动估计19
3.3基于傅立叶的对齐20
3.4逐步完善23
3.5参数运动28
4基于特征的注册33
4.1关键点检测器33
4.2特征匹配36
4.3几何配准40
4.4基于vsfeature的直接对齐46
5全球注册47
5.1捆绑包调整48
5.2视差消除51
5.3识别全景图53
6合成56
6.1选择复合面56
6.2像素选择和加权58
6.3混合64
7扩展和未解决的问题68

内容
1简介

对齐图像并将其缝合成无缝的光马赛克的算法是计算机视觉中最古老，应用最广泛的算法之一。具有“图像稳定”功能的每台摄录机都使用帧速率图像对齐。图像拼接算法可创建高分辨率的马赛克图像，用于制作当今的数字地图和卫星照片。它们还与当前出售的大多数数码相机捆绑在一起，可用于创建美丽的超广角全景。

广泛使用的图像配准算法的早期示例是Lucas和Kanade(1981)开发的基于补丁的平移对齐(光学流)技术。这种算法的变体几乎用于所有运动补偿视频压缩方案，例如MPEG和H.263(Le Gall 1991)。类似的参数运动估计算法已发现了广泛的应用，包括视频摘要(Bergen等人，1992a； Teodosio和Bender，1993； Kumar等人，1995； Irani和Anandan，1998)；视频稳定化(Hansen等人，1994)，和视频压缩(Irani等人，1995； Lee等人，1997)。还开发了用于医学成像和遥感的更复杂的图像配准算法-有关以前对图像配准技术的一些调查，请参阅(Brown，1992年，Zitov’aa和Flusser，2003年，Goshtasby，2005年)。

在摄影测量学界，基于被调查的地面控制点或手动记录的联络点的更密集的方法长期以来一直用于将航空照片记录为大规模的照相马赛克(Slama 1980)。该社区的主要进步之一是开发了束调整算法，该算法可以同时求解所有摄像机位置的位置，从而产生全局一致的解决方案(Triggs等人，1999)。产生光马赛克的反复出现的问题之一是消除了可见的接缝，这些年来，已经开发了多种技术(Milgram 1975，Milgram 1977，Peleg 1981，Davis 1998，Agarwala等2004)。

在胶片摄影中，本世纪初开发了特殊的相机来拍摄超广角全景照片，通常是在相机绕其轴旋转时通过垂直缝将胶片曝光(Meehan 1990)。在1990年代中期，图像对齐技术开始被用于从常规手持相机上构建广角无缝全景图(Mann和Picard 1994，Szeliski 1994，Chen 1995，Szeliski 1996)。该领域最近的工作已经解决了计算全局一致的对齐的需求(Szeliski和Shum 1997，Sawhney和Kumar 1999，Shum和Szeliski 2000)，消除了由于视差和物体移动引起的“重影”(Davis 1998，Shum and Szeliski 2000，Uyttendaele等人，2001，Agarwala等人，2004)，以及处理不同的暴露量(Mann和Picard，1994，Uyttendaele等人，2001，Levin等人，2004b，Agarwala等人，2004)。 (可以在(Benosman和Kang 2001)中找到其中一些论文的集合。)这些技术催生了大量的商业缝合产品(Chen 1995，Sawhney等1998)，对此可以进行评论和比较。在网上。

虽然上述大多数技术都是通过直接最小化像素间差异来工作的，但另一类算法是通过提取稀疏特征集然后将它们彼此匹配来工作的(Zoghlami等人，1997； Capel和Zisserman，1998； Cham和Cipolla 1998，Badra等1998，McLauchlan和Jaenicke 2002，Brown和Lowe 2003)。基于特征的方法的优点是对场景移动的鲁棒性更高，并且如果实施正确的方法，则可能更快。但是，它们的最大优势是“识别全景图”的能力，即自动发现无序图像集之间的邻接关系(重叠)，这使其非常适合全自动拼接由休闲用户拍摄的全景图(棕色和Lowe 2003)。

那么，图像对齐和拼接的本质问题是什么？对于图像对齐，我们必须首先确定将一个图像中的像素坐标与另一个图像中的像素坐标相关联的适当数学模型。第2节回顾了这些基本运动模型。接下来，我们必须以某种方式估计与各种图像对(或集合)相关的正确对齐方式。第三部分讨论如何将直接的像素间比较与梯度下降(以及其他优化技术)相结合来估算这些参数。第4节讨论如何在每个图像中找到独特的特征，然后有效地进行匹配以快速建立图像对之间的对应关系。当全景中存在多个图像时，必须开发出一种技术来计算全局一致的路线并有效地发现哪些图像相互重叠。这些问题在第5节中讨论。

对于图像拼接，我们必须首先选择一个最终的合成表面，在该表面上翘曲并放置所有对齐的图像(第6节)。我们还需要开发算法，以无缝融合重叠的图像，即使存在视差，镜头失真，场景运动和曝光差异(第6节)。在本调查的最后一部分中，我将讨论图像拼接的其他应用程序和开放式研究问题。

2运动模型

在注册和对齐图像之前，我们需要建立数学关系，以将像素坐标从一幅图像映射到另一幅图像。从简单的2D变换到平面透视模型，3D摄像机旋转，镜头变形以及到非平面(例如圆柱)表面的映射，各种各样的此类参数化运动模型都是可能的(Szeliski 1996)。

为了便于处理不同分辨率的图像，我们采用了计算机图形学中使用的规范化设备坐标的一种变体(Watt 1995，OpenGL-ARB 1997)。对于典型的(矩形)图像或视频帧，我们让像素坐标的长轴范围为[-1，1]，沿短轴的范围为[-a，a]，其中a是长宽比的倒数，如图1所示。¹对于宽度为W，高度为H的图像，将整数像素坐标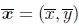映射到归一化设备坐标x =(x，y)的方程为


请注意，如果我们处理金字塔中的图像，则需要在每个抽取步骤之后将S值减半，而不是根据max(W，H)重新计算，因为(W，H)值可能会以不可预测的方式四舍五入或被截断方式。请注意，在本文的其余部分中，当引用像素坐标时，我们将使用归一化的设备坐标。

　　1在计算机图形学中，通常两个轴的范围都在[−1，1]范围内，但这需要在垂直和水平方向上使用两个不同的焦距，这使得处理纵向和横向混合图像变得更加尴尬 。

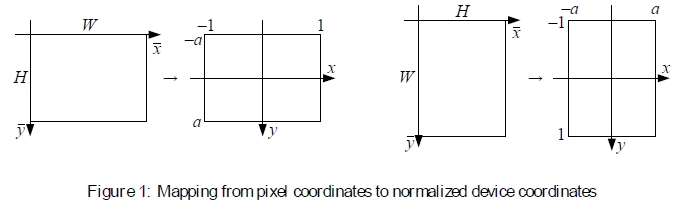
图1：从像素坐标到规范化设备坐标的映射

2.1 2D(平面)运动

定义了坐标系统后，我们现在可以描述如何转换坐标。 最简单的转换发生在2D平面中，如图2所示。

图2：基本的2D平面变换集

翻译。 二维翻译可以写成x'= x + t或

其中I是(2×2)单位矩阵，^〜x =(x，y，1)是齐次或投影2D坐标。

旋转+平移。 此变换也称为2D刚体运动或2D欧几里得变换(因为保留了欧几里得距离)。 可以写成x'= Rx + t或

其中

是RR^T = I 并且| R |的正交旋转矩阵 = 1。

缩放旋转。 也称为相似度变换，该变换可以表示为x'= sRx + t，其中s是任意比例因子。 也可以写成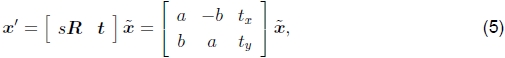

在这里我们不再要求a² + b² =1。相似度转换保留了线之间的角度。

仿射。 仿射变换写为x'= A^〜x，其中A是任意2×3矩阵，即

在仿射变换下，平行线保持平行。

投射的。 此变换(也称为透视变换或单应性)在同构坐标^〜x和^〜x'上进行操作，

其中〜表示等比例的缩放，^〜H是任意的3×3矩阵。 注意，^〜H本身是同质的，即，它仅按比例定义。 产生的齐次坐标^〜x'必须进行归一化以获得不均匀的结果x'，即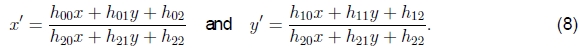

透视变换保留直线。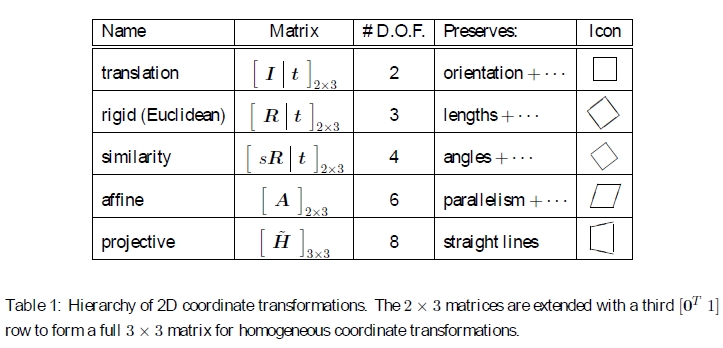

表1：2D坐标转换的层次结构。 将2×3矩阵扩展为第三行[0^T 1]，以形成用于均匀坐标变换的完整3×3矩阵。

2D转换的层次结构图2中说明了前面的转换集，表1中对此进行了概述。最简单的方法是将它们看作是一组在2D齐次坐标矢量上运行的(可能受限的)3×3矩阵。 Hartley和Zisserman(2004)对2D平面变换的层次结构进行了更详细的描述。

上面的变换形成了一组嵌套的组，即它们在组成下是封闭的，并且具有作为同一组成员的逆。 每个(简单)组都是其下更复杂组的子集。

2.2 3D转换

对于3D坐标转换，也存在类似的嵌套层次结构，可以使用4×4转换矩阵表示，具有与平移，刚体(欧几里得)和仿射变换以及同形(有时称为collineation)的3D等效项(Hartley和Zisserman 2004)。

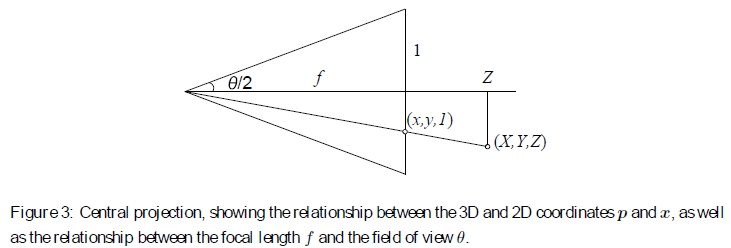
图3：中央投影，显示3D和2D坐标p和x之间的关系，以及焦距f和视场θ之间的关系。

中心投影过程是通过摄像机原点上的针孔将3D坐标p =(X，Y，Z)映射为2D坐标x =(x，y，1)到沿z轴的距离为f 的2D投影平面上，

如图3所示。(无单位)焦距f 与视场θ之间的关系为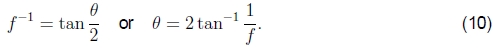

要将焦距f转换为更常用的等效35mm焦距，请将上述数值乘以17.5(35mm负片照相框的半宽度)。要将其转换为像素坐标，将其乘以S / 2(风景照片的一半宽度)。

在计算机图形学文献中，透视投影通常写为置换矩阵，该置换矩阵置换齐次4-向量p =(X，Y，Z，1)的最后两个元素，

然后缩放并转换为屏幕和z缓冲区坐标。

在计算机视觉中，传统上会丢弃z缓冲区值，因为无法在图像中感知到这些值并进行写入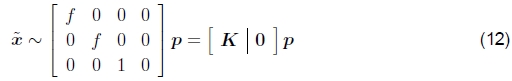

其中K = diag(f，f，1)称为内在校准矩阵。²该矩阵可以由更通用的上三角矩阵K代替，该矩阵考虑非正方形像素，偏斜和可变的光学中心位置 (Hartley and Zisserman 2004)。 但是，实际上，在拼接来自常规相机的图像时，上面使用的简单焦距缩放可提供高质量的结果。
　　2 K的最后一列通常包含光学中心(cx，cy)，但是如果我们使用归一化的设备坐标，则可以将其设置为零。

在本文中，我更喜欢使用4×4投影矩阵P，

它将均质的4-矢量p =(X，Y，Z，1)映射到一种特殊的均质屏幕矢量^〜x =(x，y，1，d)。 这使我可以将投影矩阵P的左上3×3部分表示为K(使其与计算机视觉文献兼容)，而不会完全放弃逆屏幕深度信息d(有时也称为视差d)(Okutomi and Kanade 1993)。 如下所述，后一数量对于推理3D场景的图像之间的映射是必需的。

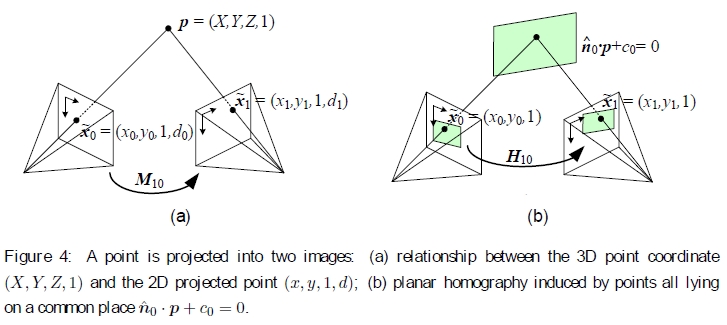
图4：将一个点投影到两个图像中：(a)3D点坐标(X，Y，Z，1)和2D投影点(x，y，1，d)之间的关系； (b)由均位于共同位置ˆn₀·p + c₀ = 0的点引起的平面单应性。

当我们从不同的相机位置和/或方向拍摄3D场景的两幅图像时会发生什么(图4a)？ 通过3D刚体(欧几里得)运动E₀的组合，将3D点p映射到摄像机0中的图像坐标^〜x0，

和透视投影P₀，

假设我们知道一个图像中像素的z缓冲区值d0，我们可以使用以下方式将其映射回3D坐标p

然后将其投影到另一个图像中

不幸的是，我们通常无法访问常规摄影图像中像素的深度坐标。 但是，对于平面场景，我们可以用通用平面方程 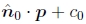代替(13)中的P₀的最后一行，该方程将平面上的点映射到d₀ = 0值(图4b)。 然后，如果我们设置d₀ = 0，则我们可以忽略(17)中M₁₀的最后一列以及它的最后一行，因为我们不在乎最终的z缓冲区深度。 映射方程式(17)因此简化为

其中^〜H₁₀是一般的3×3单应性矩阵，而^〜x₁和^〜x₀现在是2D齐次坐标(即3-矢量)(Szeliski 1994，Szeliski 1996)。³这证明了将8参数单应性用作 平面场景镶嵌的通用对齐模型(Mann and Picard 1994，Szeliski 1996)。⁴
　　3对于离开参考平面的点，我们得到了平面外视差运动，这就是为什么这种表示通常被称为平面加视差表示的原因(Sawhney 1994，Szeliski和Coughlan 1994，Kumar等人，1994)。

　　4请注意，对于单对图像，一组刚性相机正在查看3D平面这一事实并不会减少自由度的总数。 但是，对于从校准相机拍摄的大量平面图像(例如白板)，我们可以通过假设平面位于标准位置来将每个图像的自由度数从8减少到6。 例如z = 1)。

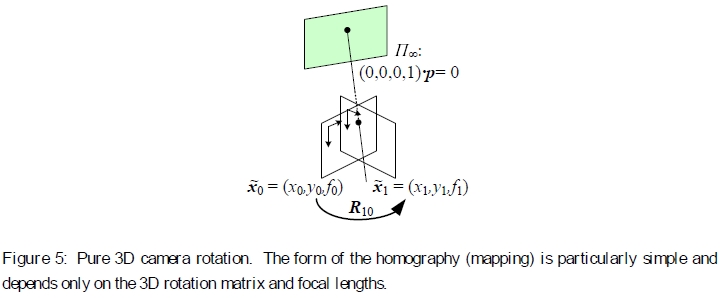
图5：纯3D摄影机旋转。单应性(映射)的形式是特别简单且仅取决于三维旋转矩阵和焦距。

旋转全景图更有趣的情况是相机进行纯旋转(图5)，这等效于假设所有点都距离相机很远，即在无穷远的平面上。 设置t₀ = t₁ = 0，我们得到简化的3×3单应性

其中K_k = diag(f_k，f_k，1)是简化的相机固有矩阵(Szeliski 1996)。 这也可以重写为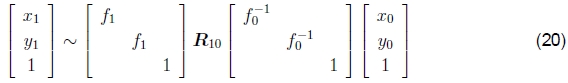

或

这揭示了映射方程式的简单性，并使所有运动参数明确。 因此，我们获得了与焦距f已知，固定或可变的情况相对应的3、4或5参数3D旋转运动模型，而不是与一对图像相关的一般8参数单应性(Szeliski and Shum 1997)。 估计与每个图像关联的3D旋转矩阵(以及可选的焦距)本质上比估计完整的8-d.o.f.更稳定。 单应性，这使其成为大规模图像拼接算法的选择方法(Szeliski和Shum 1997，Shum和Szeliski 2000，Brown和Lowe 2003)。

参数化3D旋转。 如果我们要使用旋转和焦距的组合来表示全景图，那么代表旋转本身的最佳方法是什么？ 选项包括：
•完整的3×3矩阵R，每次更新后都必须重新正交化；
•欧拉角(α，β，γ)是个坏主意，因为您不能始终平稳地从一个旋转移动到另一个旋转。
•轴/角度(或指数扭曲)表示形式，代表轴ˆn和旋转角θ或两者之积的旋转，

它具有最少数目的3个参数，但仍不是唯一的；
•和单位四元数，代表具有4位向量的旋转，

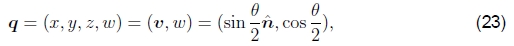
其中ˆn和θ是旋转轴和角度。

对应于围绕轴ˆn旋转θ的旋转矩阵为

这就是Rodriguez的公式(Ayache 1989)，[ˆn]×是叉积算子的矩阵形式，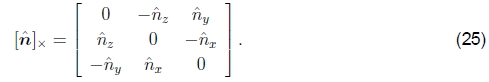

对于小(无限小)旋转，旋转减小为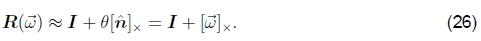

使用三角恒等式

和

罗德里格斯的四元数公式可以转换为

这建议使用一系列叉积，标度和加法，通过四元数旋转矢量的快速方法。 由此，我们可以得出R(q)的常用公式是q =(x，y，z，w)的函数，

通过用(x² + w²-y²-z²)等替换1-2(y² + z²)等人，可以使对角线项更加对称。

在轴/角度表示和四元数之间，我通常更喜欢单位四元数，因为它们具有很好的代数，可以轻松地乘积(组合)，比率(旋转变化)和线性插值(Shoemake 1985)。 例如，两个四元数q₀ =(v₀，w₀)和q₁ =(v₁，w₁)的乘积为

具有R(q₂)= R(q₀)R(q₁)的属性。 (请注意，四元数乘法不是可交换的，就像3D旋转和矩阵乘法不是可交换的一样。)对四元数取反也很容易：只需翻转v或w的符号(但不能同时翻转！)。 但是，当需要更新旋转估计值时，我将使用增量形式的轴/角度表示形式(26)，如第4.3节所述。

2.3圆柱坐标和球坐标

使用单应性或3D运动对齐图像的另一种方法是先将图像扭曲为圆柱坐标，然后使用纯平移模型对齐它们(Szeliski 1994，Chen 1995)。 不幸的是，这仅在所有图像均使用水平摄像机或已知倾斜角度拍摄的情况下才有效。

现在假设摄像机处于其标准位置，即其旋转矩阵为恒等式R = I，以使光轴与z轴对齐且y轴垂直对齐。 因此，对应于(x，y)像素的3D射线为(x，y，f)。

我们希望将此图像投影到单位半径的圆柱表面上(Szeliski 1994)。 该表面上的点由角度θ和高度h参数化，其中3D圆柱坐标对应于(θ，h)，由

图6：从3D投影到圆柱坐标和球坐标。

如图6a所示。 根据这种对应关系，我们可以计算变形或映射坐标的公式(Szeliski and Shum 1997)，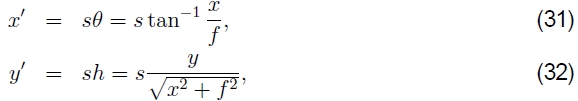

其中s是任意缩放比例因子(有时称为圆柱体的半径)，可以将其设置为s = f，以最大程度地减小图像中心附近的失真(缩放比例)。⁵该映射方程式的逆公式为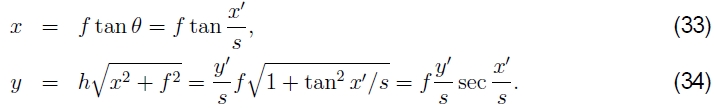

　　5根据所需的输出全景分辨率，也可以将最终合成表面的比例尺设置为更大或更小值(请参见§6)。

图像也可以投影到球形表面上(Szeliski and Shum 1997)，如果最终的全景图包括一个完整的球面或半球视图，而不是仅一个圆柱形的条带，则这很有用。 在这种情况下，用两个角度(θ，φ)对球进行参数化，其中3D球坐标由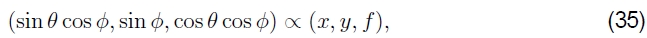

如图6b所示。 坐标之间的对应关系现在由(Szeliski and Shum 1997)给出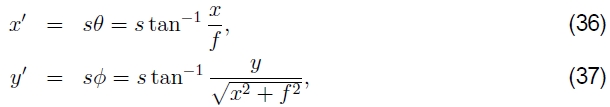

而逆是由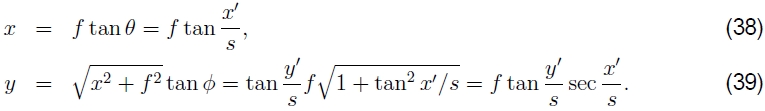

请注意，从(35)生成缩放的(x，y，z)方向，然后将透视图除以z，然后按f缩放可能会更简单。

当已知相机水平且仅绕其垂直轴旋转时，通常会使用圆柱图像拼接算法(Chen 1995)。 在这种情况下，不同旋转角度的图像通过纯水平平移相关联。⁶这使它作为计算机视觉入门课程中的入门级项目具有吸引力，因为透视图对齐算法(第3.5和第4.3节)的全部复杂性可以 被避免。 图7显示了来自水平旋转全景的两个圆柱扭曲图像如何通过纯平移进行关联(Szeliski和Shum 1997)。

　　6有时可以使用垂直平移来补偿小的垂直倾斜。

图7：圆柱全景图的示例：(a)两个通过水平平移关联的圆柱扭曲图像； (b)由一系列图像合成的圆柱全景图的一部分。

专业的全景摄影师有时还会使用云台，这样可以轻松控制倾斜并在旋转角度的特定定位点停下来。这不仅确保了视野均匀覆盖，并具有所需的图像重叠量，而且还可以使用圆柱或球面坐标和纯平移拼接图像。在这种情况下，在将像素坐标(x，y，f)投影到圆柱坐标或球坐标之前，必须先使用已知的倾斜和平移角度对其进行旋转(Chen 1995)。具有一个大致已知的摇摄角度也使计算对齐更加容易，因为所有输入图像的粗略相对位置都是提前知道的，从而可以减小对齐的搜索范围。图8显示了展开到球体表面上的完整3D旋转全景图(Szeliski and Shum 1997)。

图8：由54张照片构成的球形全景的示例。

值得一提的最后一个坐标图是极坐标图，其中北极沿着光轴而不是垂直轴，

其中r =√(x²+ y²⁾是(x，y)平面中的径向距离，而sφ在(x'，y')平面中起类似的作用。 如第2.4节所述，此映射为某些种类的广角全景图提供了有吸引力的可视化表面，并且还是由鱼眼镜头引起的失真的良好模型。请注意，对于(x，y)的较小值，映射方程式如何简化为x'≈sx / z，这表明s的作用类似于焦距f。

2.4镜头变形

图9：径向镜片变形的示例：(a)镜筒，(b)枕形和(c)鱼眼。 鱼眼的图像从一侧到另一侧几乎覆盖了整个180°。

使用广角镜拍摄图像时，通常需要对镜头畸变(例如径向畸变)建模。 径向畸变模型表示，观察到的图像中的坐标偏移(桶形畸变)或朝向(枕形畸变)图像中心，偏移量与它们的径向距离成正比(图9a–b)。 最简单的径向失真模型使用低阶多项式，例如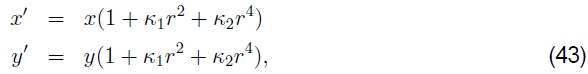

其中将r²=x²+y²和κ₁和κ₂称为径向变形参数(Brown 1971，Slama 1980)。⁷ 更复杂的变形模型还包括切向(偏心)变形(Slama 1980)，但是对于消费者级别的缝合来说通常不需要。

　　7有时x和x'之间的关系以相反的方式表示，即使用右侧的准备好的(最终)坐标。

可以使用多种技术来估计给定透镜的径向畸变参数。最简单也是最有用的方法之一是拍摄具有很多直线的场景图像，尤其是与图像边缘对齐并靠近图像边缘的直线。然后可以调整径向畸变参数，直到图像中的所有线都笔直为止，这通常称为铅垂线法(Brown 1971，Kang 2001，El-Melegy和Farag 2003)。

另一种方法是使用几个重叠的图像，并将径向变形参数的估计与图像对齐过程结合在一起。 Sawhney和Kumar(1999)在粗糙到精细的策略中结合了二次径向畸变校正项，使用了运动模型的层次结构(平移，仿射，射影)。他们使用直接(基于强度)最小化来计算对齐。 Stein(1997)将基于特征的方法与一般的3D运动模型(以及二次径向失真)结合使用，与无视差的旋转全景图相比，它需要更多的匹配项，但可能更通用。最近的方法有时同时计算未知的固有参数和径向变形系数，其中可能包括高阶项或更复杂的有理或非参数形式(Claus和Fitzgibbon 2005，Sturm 2005，Thirthala和Pollefeys 2005，Barreto和Daniilidis 2005 ，Hartley and Kang 2005，Steele and Jaynes 2006，Tardif et al。2006b)。

鱼眼镜头与传统的径向畸变多项式模型需要不同的模型(图9c)。取而代之的是，鱼眼镜头的表现近似于等距投影机的角度与光轴的夹角(Xiong and Turkowski 1997)，与等式(40-42)描述的极投影相同。Xiong和Turkowski(1997)描述了如何通过在φ中添加额外的二次校正来扩展该模型，以及如何从一组重叠的鱼眼中估计未知参数(投影中心，比例因子s等)。使用直接(基于强度)非线性最小化算法的图像。

存在甚至更一般的镜头畸变模型。例如，可以将任何透镜表示为像素到空间光线的映射(Gremban等人，1988； Champleboux等人，1992； Grossberg插值平滑函数，例如样条曲线)(Goshtasby 1989，Champleboux等人，1992)。


3直接(基于像素)对齐

一旦我们选择了合适的运动模型来描述一对图像之间的对准，就需要设计某种方法来估计其参数。一种方法是使图像彼此相对移动或扭曲，并查看像素的一致性。与下一节中介绍的基于特征的方法相反，使用像素间匹配的方法通常称为直接方法。

要使用直接方法，必须首先选择合适的误差度量来比较图像。一旦确定了这一点，就必须设计一种合适的搜索技术。最简单的技术是穷举尝试所有可能的比对，即进行完整搜索。在实践中，这可能太慢，因此已经开发了基于图像金字塔的分层粗到细技术。可替代地，可以使用傅立叶变换来加速计算。为了获得对准中的亚像素精度，通常使用基于图像函数的泰勒级数展开的增量方法。这些也可以应用于参数运动模型。这些技术中的每一种将在下面更详细地描述。

3.1错误指标

在两个图像之间建立对齐的最简单方法是相对于另一个图像移动一个图像。给定在离散像素位置{x_i = (x_i, y_i)} 采样的模板图像I₀(x)，我们希望找到它在图像I₁(x)中的位置。解决此问题的最小二乘方法是找出平方差和(SSD)函数的最小值

其中u = (u, v)是位移，而e_i = I₁(x_i+ u)- I₀(x_i) 被称为残差误差(或视频编码文献中的位移帧差异)。⁸(目前，我们忽略了I₀的某些部分可能位于I₁边界之外或看不见的可能性) 。)

　　8使用最小二乘法的通常理由是，它是针对高斯噪声的最佳估计。 请参阅下面有关健壮替代方案的讨论。

通常，位移u可以是分数，因此必须对图像I₁(x)应用合适的插值函数。实际上，通常使用双线性插值，但是双三次插值应该会产生更好的结果。可以通过将所有三个颜色通道之间的差异求和来处理彩色图像，尽管也可以先将图像转换为不同的颜色空间，也可以仅使用亮度(这通常在视频编码器中完成)。

健壮的误差度量我们可以通过用健壮的函数p(e_i)(Huber 1981，Hampel et al。1986，Black and Anandan 1996，Stewart 1999)替换平方误差项，使上述误差度量对离群值更具鲁棒性，从而获得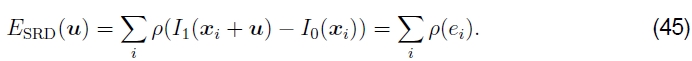

健壮的范式p(e)是一个增长速度小于与最小二乘相关的二次惩罚的函数。有时由于其速度而有时在视频编码的运动估计中使用的此类功能是绝对差之和(SAD)指标，即

但是，由于此函数在原点不可区分，因此不适用于§3.4中介绍的渐变方法。

取而代之的是，通常使用平滑变化的函数，该函数对于较小的值是平方的，但在远离原点的位置增长得更慢。Black and Rangarajan(1996)讨论了许多此类函数，包括Geman-McClure函数，

其中a是可以视为异常值阈值的常数。阈值的适当值本身可以使用稳健的统计数据得出(Huber 1981，Hampel等人1986，Rousseeuw和Leroy 1987)，例如，通过计算绝对差的中位数，MAD = med_i |e_i| 并乘以1.4得到一个非离群噪声过程的标准偏差的可靠估计(Stewart 1999)。

空间变化的权重。上面的误差度量忽略了以下事实：对于给定的对齐方式，要比较的某些像素可能位于原始图像边界之外。此外，我们可能希望部分或全部降低某些像素的贡献。例如，我们可能想从考虑中选择性地“擦除”图像的某些部分，例如，在拼接已切掉不需要的前景对象的马赛克时。对于诸如背景稳定化之类的应用，我们可能希望减轻图像的中间部分的重量，该中间部分通常包含由相机跟踪的独立移动的对象。

所有这些任务都可以通过将空间变化的每像素权重值与匹配的两个图像中的每个图像相关联来完成。然后，错误度量成为加权(或加窗)的SSD函数

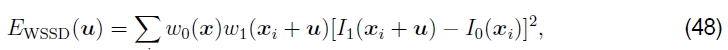
其中加权函数w₀和w₁在图像的有效范围之外为零。

如果允许大范围的潜在运动，则上述度量可能会偏向于较小的重叠解。为了抵消这种偏差，可以将开窗的SSD得分除以重叠区域

计算每像素(或均值)平方像素误差。 该数量的平方根是均方根强度误差

在比较研究中经常看到报道。

偏差和增益(曝光差异)。通常，没有以相同的曝光拍摄对准的两个图像。两个图像之间线性(精细)强度变化的简单模型是偏置和增益模型，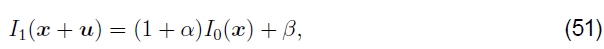

其中β是偏差，α是收益(Lucas和Kanade 1981，Gennert 1988，Fuh和Maragos 1991，Baker等人2003b)。最小二乘公式变为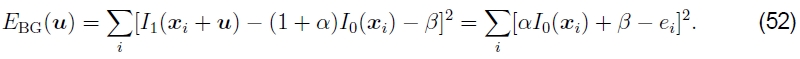

与其采取相应补丁之间的简单平方差，不如执行线性回归，这会变得更加昂贵。请注意，对于彩色图像，可能需要为每个彩色通道估计不同的偏差和增益，以补偿某些数码相机执行的自动色彩校正。

(Jia and Tang 2003)提出了一个更通用的(空间变化的非参数)强度变化模型，该模型是在配准过程中计算的。这对于处理局部变化(例如由广角镜引起的渐晕)很有用。也可以在比较图像值之前对图像进行预处理，例如，使用带通滤波图像(Burt和Adelson 1983，Bergen等人1992a)或使用其他局部变换，例如直方图或秩变换(Cox等)。等人，1995年； Zabih和Woodfill，1994年)，或最大化相互信息(Viola和Wells III，1995年，Kim等人，2003年)。

相关性。 采取强度差异的另一种方法是执行关联，即最大化两个对齐图像的乘积(或互相关)，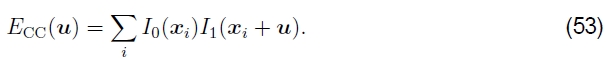

乍一看，这似乎使偏置和增益建模变得不必要，因为图像将更倾向于对齐，而无论它们的相对比例和偏移如何。 但是，实际上并非如此。 如果I₁(x)中存在非常明亮的色块，则最大乘积实际上可能位于该区域。

因此，更常用归一化互相关，

其中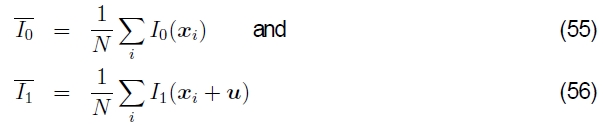

是相应补丁的平均图像，N是补丁中的像素数。 归一化互相关分数始终保证在[-1，1]范围内，这使它在某些更高级别的应用程序中更易于处理(例如确定哪些补丁真正匹配)。 但是请注意，如果两个色块中的任何一个色差为零，则NCC得分不确定(实际上，对于嘈杂的低对比度区域，其性能会降低)。

3.2分层运动估计

既然我们已经定义了一个对齐成本函数进行优化，我们如何找到它的最小值？最简单的解决方案是使用整数或子像素步长对一定范围的位移进行全面搜索。这通常是在运动补偿视频压缩中用于块匹配的方法，其中探索了可能的运动范围(例如±16像素)。⁹

　　9在立体匹配中，几乎总是执行对所有可能的视差(即平面扫描)的显式搜索，因为由于潜在位移的一维性质，搜索假设的数量要少得多(Scharstein和Szeliski 2002)。

为了加速该搜索过程，经常使用分层运动估计，其中首先构造了图像金字塔，然后首先在较粗糙的级别上执行较少数量的离散像素(对应于相同的运动范围)的搜索(Quam 1984，Anandan 1989，Bergen et al。1992a)。然后，可以从金字塔的一个级别进行运动估计，以在下一个更细的级别初始化较小的局部搜索。虽然不能保证产生与完全搜索相同的结果，但通常效果几乎一样，而且速度更快。
更正式地，让

是通过对级别 l-1的图像进行平滑采样(预滤波)获得的级别l 抽取的图像。 在最粗糙的水平上，我们搜索最佳位移u^(l)，以使图像I^(l)₀和I^(l)₁之间的差异最小。 通常使用对位移u^(l)∈2^-l [−S，S] ²的某个范围进行全面搜索来完成此操作(其中S是在最佳(原始)分辨率级别上所需的搜索范围)，然后可选地跟随 §3.4中所述的增量优化步骤。

一旦估计了合适的运动矢量，就可以用来预测可能的位移

下一个更高的水平。¹⁰ 然后，在更狭窄的位移范围(例如ˆu^(l-1)±1)上以更细的层次重复位移的搜索，再次有选择地与增量细化步骤结合使用(Anandan 1989)。 在(Bergen et al。1992a)中可以找到对整个过程的一个很好的描述，扩展到参数运动估计(第3.5节)。

　　10只有在整数像素坐标中定义了位移时才需要将位移加倍，这是文献中的常见情况，例如(Bergen et al。1992a)。 如果改用规范化的设备坐标(§2)，则位移(和搜索范围)不必在各个级别之间变化，尽管步长需要进行调整(以保持大约1个像素的搜索步长)。

3.3基于傅立叶的对齐

当搜索范围对应于较大图像的重要部分时(如图像拼接的情况)，分层方法可能效果不佳，因为在重要特征被模糊掉之前，通常不可能对表示进行过多的粗化。在这种情况下，基于傅里叶的方法可能更可取。

基于傅立叶的对齐方式依赖于这样一个事实，即移位信号的傅立叶变换具有与原始信号相同的幅度，但线性变化的相位，即

其中f是傅立叶变换的矢量值频率，我们使用书法符号L₁(f)= F{I₁(x)}表示信号的傅立叶变换(Oppenheim et al。1999，p.57)。

傅立叶变换的另一个有用特性是，空间域中的卷积对应于傅立叶域中的乘法(Oppenheim等人，1999，第58页)。因此，互相关函数E_cc的傅立叶变换可以写为

其中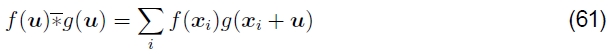

是相关函数，即一个信号与另一个信号的反卷积，而L₁*(f) 是复共轭L₁(f)。 (这是因为卷积被定义为一个信号与另一个信号的求和(Oppenheim等人，1999)。)

因此，为了在u的所有可能值的范围内有效地评估E_cc，我们采用了u的傅立叶变换。分别将图像I₀(x)和I₁(x)都相乘(在第二个共轭之后)，并对结果进行逆变换。快速傅立叶变换算法可以在O(NM log NM) 操作中计算N*M图像的变换(Oppenheim等人1999)。当考虑整个图像重叠范围时，这可能比进行完整搜索所需的O(N²M²) 操作快得多。

尽管基于傅立叶的卷积通常用于加速图像相关性的计算，但它也可以用于加速平方差函数之和(及其变体)。考虑(44)中给出的SSD公式。它的傅立叶变换可以写成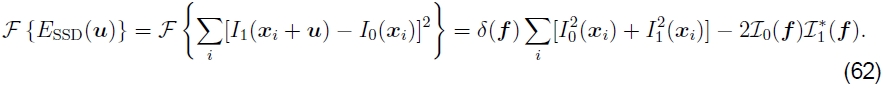

因此，可以通过取两倍的相关函数并将其从两个图像中的能量之和中减去来计算SSD函数。

窗口相关。 不幸的是，傅立叶卷积定理仅适用于在两个图像中所有像素上进行x_i 求和时，当访问原始边界之外的像素时使用图像的圆移。 尽管这对于较小的偏移和大小相对应的图像是可以接受的，但是当图像重叠少量或一个图像是另一个图像的一小部分时，这是没有意义的。

在这种情况下，应将互相关函数替换为加窗(加权)互相关函数，

其中加权函数w₀和w₁在图像的有效范围之外为零，并且对两个图像进行填充，以便循环移位返回原始图像边界之外的0值。

一个更有趣的情况是在(48)中引入的加权SSD函数的计算

因此，所得表达式的傅立叶变换为

其中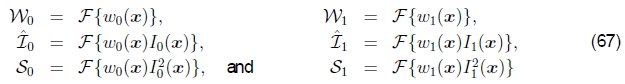

加权函数以及加权原始和平方图像信号的傅立叶变换。因此，以一些额外的图像乘法和傅立叶变换为代价，可以计算出正确的加窗SSD函数。 (据我所知，我以前没有看过这个公式，但是几年来我一直在教给学生。)

相同的推导可以应用于平方差函数E_BG的偏差增益校正和。同样，可以使用傅立叶变换来有效地计算在偏置和增益参数中执行线性回归所需的所有相关性，以便为每个电位偏移估算曝光补偿的差异。

相位相关。 有时用于运动估计的规则相关性(60)的一种变体是相位相关性(Kuglin and Hines 1975，Brown 1992)。 在此，通过将(60)中的每个频率乘积除以傅里叶变换的幅度，将匹配的两个信号的频谱变白，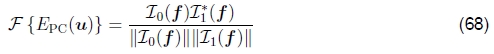

在进行最终的傅立叶逆变换之前。 对于具有完美(循环)位移的无噪声信号，我们有I₁(x + u)= I₀(x)，因此从(59)得到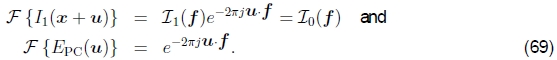

因此，相位相关性的输出(在理想条件下)是位于u正确值处的单个尖峰(脉冲)，这(原则上)使查找正确的估计更为容易。

相位相关在某些方面的表现优于常规相关，但这种行为取决于信号和噪声的特性。如果原始图像被窄频带中的噪声(例如，低频噪声或峰值频率“嗡嗡声”)污染，则白化过程会有效地消除这些区域中的噪声。但是，降低性能。最近，梯度互相关已经成为相位相关的有前途的替代方法(Argyriou and Vlachos 2003)，尽管可能需要进一步的系统研究。Fleet和Jepson(1990)还研究了相位相关性，作为估计一般光学流和立体视差的方法。

旋转和缩放。尽管基于傅立叶的对齐方式主要用于估计图像之间的平移，但在某些有限条件下，它也可以用于估算面内旋转和缩放。考虑两个纯粹通过旋转相关的图像，即

如果我们将图像重新采样为极坐标，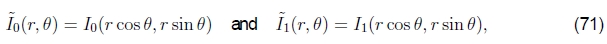

我们获得

然后可以使用基于FFT移位的技术来估计所需的旋转。
如果两个图像也按比例相关，

我们可以重新采样为对数极坐标，

获得

在这种情况下，必须注意选择合理采样原始图像的s值范围。

对于少量翻译的图像，

De Castro和Morandi(1987)提出了一种巧妙的解决方案，该解决方案使用几个步骤来估计未知参数。 首先，将两个图像都转换为傅立叶域，并且仅保留已转换图像的大小。 原则上，傅立叶幅值图像对图像平面中的平移不敏感(尽管通常会出现关于边框效果的警告)。 接下来，使用极坐标或对数极坐标表示，将两个幅值图像旋转并按比例对齐。 一旦估计了旋转和比例，就可以对其中一张图像进行旋转和缩放，然后可以应用常规的平移算法来估计平移。

不幸的是，此技巧仅在图像重叠大(平移运动小)时适用。 对于补丁或图像的更一般的运动，需要使用第3.5节所述的参数运动估计器或第4节所述的基于特征的方法。

3.4逐步完善

到目前为止描述的技术可以估计到最近像素(如果使用较小的搜索步骤，则可能是分数像素)的平移对齐。通常，图像稳定和缝合应用需要更高的精度才能获得可接受的结果。

为了获得更好的亚像素估计，我们可以使用以下几种技术之一(Tian和Huhns 1986)。一种可能是，根据迄今为止找到的最佳值，对(u, v)的几个离散(整数或小数)值进行评估，然后对匹配分数进行插值，以求出解析最小值。

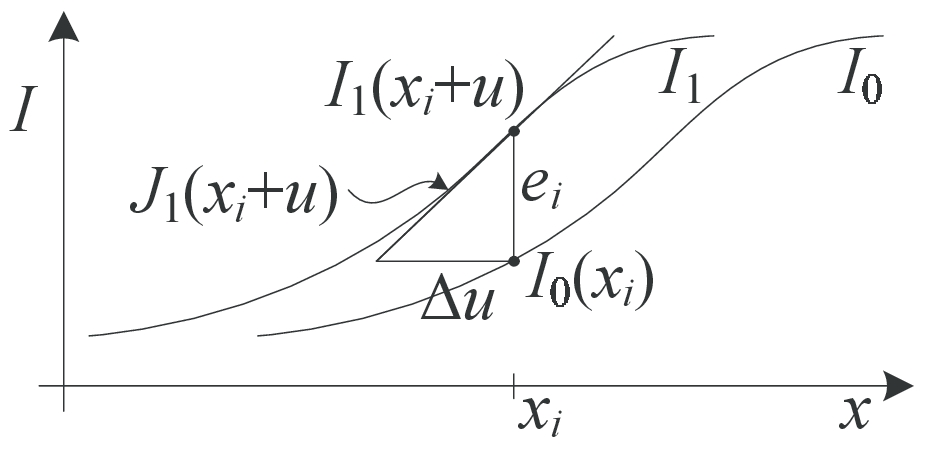
图10：函数的泰勒级数逼近和光流校正量的增量计算。 J₁(x_i + u)是(x_i + u)处的图像梯度，e_i是当前强度差。

Lucas和Kanade(1981)首次提出的一种更常用的方法是使用图像函数的泰勒级数展开对SSD能量函数(44)进行梯度下降(图10)，

其中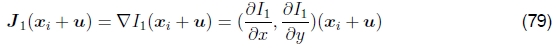

是(x_i+u)处的图像渐变，并且

首先在(44)中介绍的是电流强度误差。¹¹

　　11我们遵循通常在机器人技术和(贝克和马修斯，2004年)中使用的约定，即关于(列)向量的导数产生行向量，因此公式中需要较少的转置。

通过求解相关的正态方程，可以使上述最小二乘问题最小化(Golub and Van Loan 1996)，

其中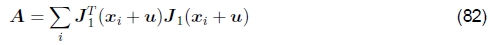

和

分别称为Hessian和梯度加权残差向量(的Gauss-Newton逼近)。¹² 这些矩阵通常也表示为

　　12真正的Hessian是误差函数E的完整二阶导数，它可能不是正定的。

其中I_x和I_y中的下标表示空间导数，而I_t称为时间导数，如果我们正在计算视频序列中的瞬时速度，这是有意义的。

可以与估计I₁(x_i + u)所需的图像扭曲同时评估J₁(x_i + u)所需的梯度，实际上，通常将其计算为图像插值的副产品。 如果您担心效率问题，可以将这些渐变替换为模板图片中的渐变，

由于接近正确的对齐方式，因此模板和目标图像应该看起来相似。 这具有允许对Hessian和Jacobian图像进行预计算的优势，这可以节省大量计算量(Hager和Belhumeur 1998，Baker和Matthews 2004)。 通过将用于计算ei的变形图像I₁(x_i + u)写为(80)中的子像素插值滤波器与I₁中的离散样本的卷积，可以进一步减少计算量(Peleg and Rav-Acha 2006 )。 预计算梯度场和I₁的偏移版本之间的内积，可以在恒定时间内(与像素数无关)执行e_i的迭代重新计算。

上述增量更新规则的有效性取决于泰勒级数逼近的质量。当远离真实位移(例如1-2像素)时，可能需要几次迭代。 (但是，可以使用最小二乘方拟合一系列较大的位移来估计J1的值，以增加会聚范围(Jurie和Dhome 2002)。)在正确的解附近开始，通常只需几次迭代即可。常用的停止标准是监视位移校正||u||的大小，并在其降低到某个阈值(例如像素的1/10 th)以下时停止。对于较大的运动，通常将增量更新规则与分层的粗到细搜索策略结合在一起，如第3.2节所述。

调节和光圈问题。有时，线性系统(81)的反转条件不佳，因为要对齐的贴片中缺少二维纹理。一个常见的例子是孔径问题，最早是在光学流的一些早期论文中确定的(Horn和Schunck 1981)，然后由Anandan(1989)进行了更广泛的研究。考虑一个图像块，该图像块由向右移动的倾斜边缘组成(图11)。在这种情况下，只能可靠地恢复速​​度(位移)的法线分量。这在(81)中表现为秩秩矩阵A，即其较小特征值非常接近于零的矩阵。¹³

　　13矩阵A通过构造始终保证是对称的正半定数，即它具有真实的非负特征值。

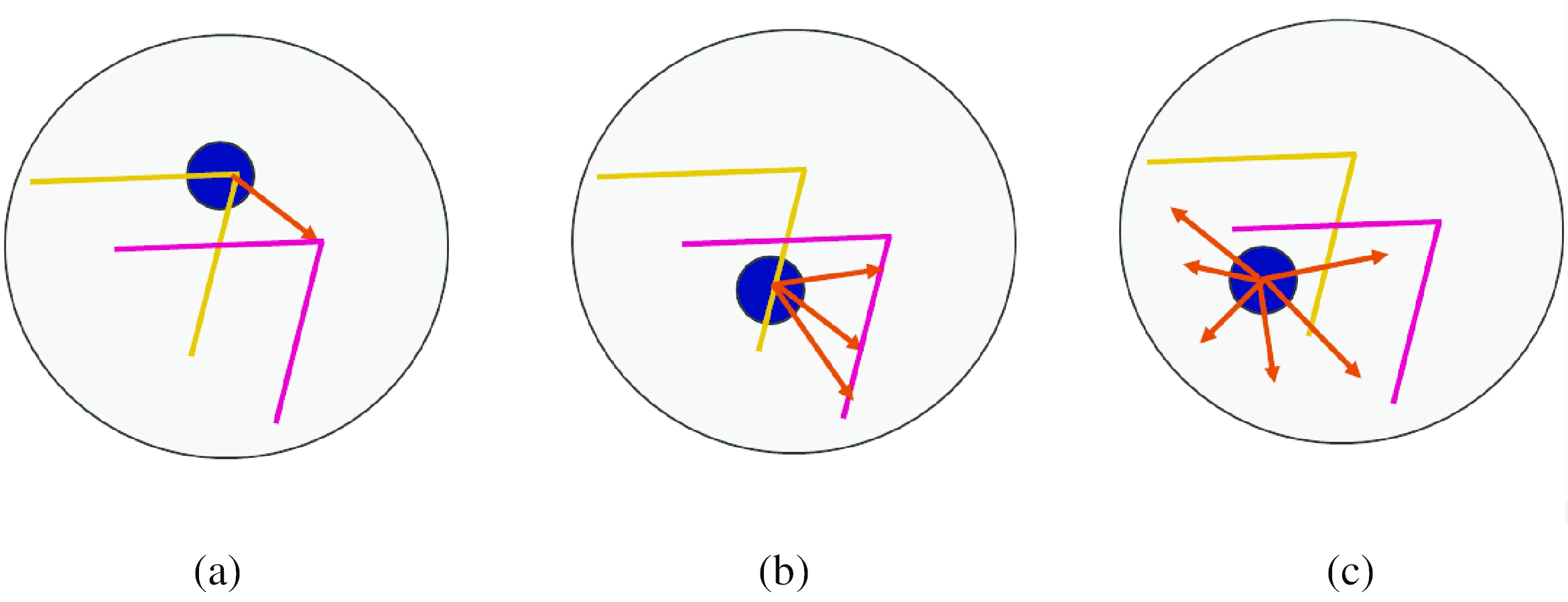
图11：不同图像斑块的光圈问题：(a)稳定(“角状”)流动； (b)经典光圈问题(理发极幻觉)； (c)无纹理的区域。

求解方程(81)时，沿边缘的位移分量的调节条件很差，并且可能会在较小的噪声干扰下产生错误的猜测。缓解此问题的一种方法是在预期的运动范围上添加先验(软约束)(Simoncelli等人，1991； Baker等人，2004； Govindu 2006)。这可以通过向A的对角线添加一个较小的值来实现，这实际上会使解决方案偏向较小的值，该较小的值仍然(大部分)使平方误差最小。

但是，例如，在使用简单的(固定的)二次函数时(例如，Simoncelli等人，1991)，假定的纯高斯模型在实践中并不总是成立，例如，由于沿强边的混叠(Triggs，2004)。因此，在进行矩阵求逆之前，应将较大特征值的一小部分(例如5％)添加到较小特征值中，这是明智的做法。

不确定性建模可以使用不确定性模型更正式地捕获特定基于补丁的运动估计的可靠性。 最简单的此类模型是协方差矩阵，该协方差矩阵捕获所有可能方向上运动估计中的预期方差。 在少量加性高斯噪声下，可以证明协方差矩阵Σu与Hessian A的逆成比例，

其中σ_n²是加性高斯噪声的方差(Anandan 1989，Matthies et al.1989，Szeliski 1989)。对于较大量的噪声，由(78)中的Lucas-Kanade算法执行的线性化仅是近似的，因此上述数量成为真实协方差的Cramer-Rao下界。因此，现在可以将Hessian A的最小和最大特征值解释为运动的最小和最大方向上的(缩放)逆方差。 (可以在(Steele和Jaynes 2005)中找到使用更逼真的图像噪声模型进行的更详细的分析。)

偏差和增益，加权以及可靠的误差指标。Lucas-Kanade更新规则也可以应用于偏置增益方程式(52)，以获得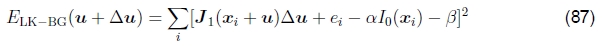

(Lucas and Kanade 1981，Gennert 1988，Fuh and Maragos 1991，Baker等人2003b)。可以求解所得的等式系统，以同时估算平移位移更新以及偏置和增益参数β和α。¹⁴

　　14在实践中，有可能去耦偏置增益和运动更新参数，即解决两个独立的2×2系统，这要快一些。

对于具有线性外观变化的图像(模板)，可以得出相似的公式，

其中是B_j(x)基础图像，λ_j是未知系数(Hager和Belhumeur 1998，Baker等人2003a，Baker等人2003b)。潜在的线性外观变化包括光照变化(Hager和Belhumeur 1998)和小的非刚性变形(Black和Jepson 1998)。

也可以使用Lucas-Kanade算法的加权(窗口式)版本，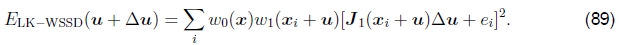

请注意，此处从原始加权SSD函数(48)导出Lucas-Kanade更新时，我们忽略了w₁(x_i + u)加权函数相对于u的导数，这在实践中通常是可以接受的，特别是在 加权函数是具有相对较少转换的二进制掩码。

Baker等人(2003a)仅使用w0(x)项，如果两个图像具有相同的范围并且在重叠区域中没有(独立)切口，则这是合理的。 他们还讨论了使权重与∇I(x)成比例的想法，这对于非常嘈杂的图像(梯度本身很嘈杂)很有帮助。 由研究最小光通量(运动)估计的其他研究人员也进行了类似的观察，以总最小二乘法(Huffel和Vandewalle 1991)表示(Weber和Malik 1995，Bab-Hadiashar和Suter 1998，Mühlich和Mester 1998)。 最后，贝克(Baker)等人(2003a)表明，即使仅使用5％-10％的像素，仅对最可靠(最高梯度)的像素进行评估(89)也不会显着降低足够大图像的性能。 (这个想法最初是由Dellaert和Collins(1999)提出的，他们使用了更为复杂的选择标准。)

Lucas-Kanade增量精炼步骤也可以应用于第3.1节中引入的健壮误差度量，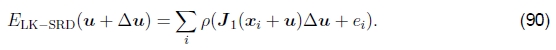

我们可以利用此函数的导数w.r.t. u并将其设置为0，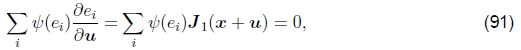

其中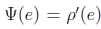是ρ的导数。如果我们引入一个权重函数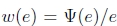，我们可以这样写：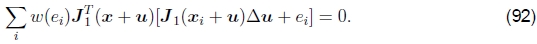

这导致迭代重新加权最小二乘算法，该算法在计算权重函数w(e_i)和解决上述加权最小二乘问题之间交替进行(Huber 1981，Stewart 1999)。可以在(Sawhney和Ayer 1996，Black和Anandan 1996，Black和Rangarajan 1996，Baker等2003a)和关于稳健统计的教科书和教程中找到替代增量鲁棒最小二乘算法(Huber 1981，Hampel等1986，Rousseeuw (Leroy，1987； Stewart，1999)。

3.5参数运动

 如第2节所述，许多图像对齐任务(例如使用手持式摄像机进行图像拼接)要求使用更复杂的运动模型。 由于这些模型通常比纯转换具有更多的参数，因此无法在可能的值范围内进行全面搜索。 相反，可以将增量Lucas-Kanade算法推广到参数化运动模型，并与分层搜索算法结合使用(Lucas和Kanade 1981，Rehg和Witkin 1991，Fuh和Maragos 1991，Bergen等1992a，Baker和Matthews 2004 )。

对于参量运动，我们使用一个由低维向量p参数化的空间变化的运动场或对应图x′(x; p)，而不是使用单个常数转换向量u，其中x′可以是任何运动 §2中介绍的模型。 现在，参数增量运动更新规则变为

其中雅可比Jacobian现在为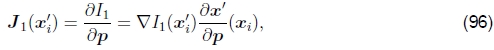

即图像梯度∇I₁与对应字段的雅可比行列式 J_x' = ∂x′/∂p 的乘积。

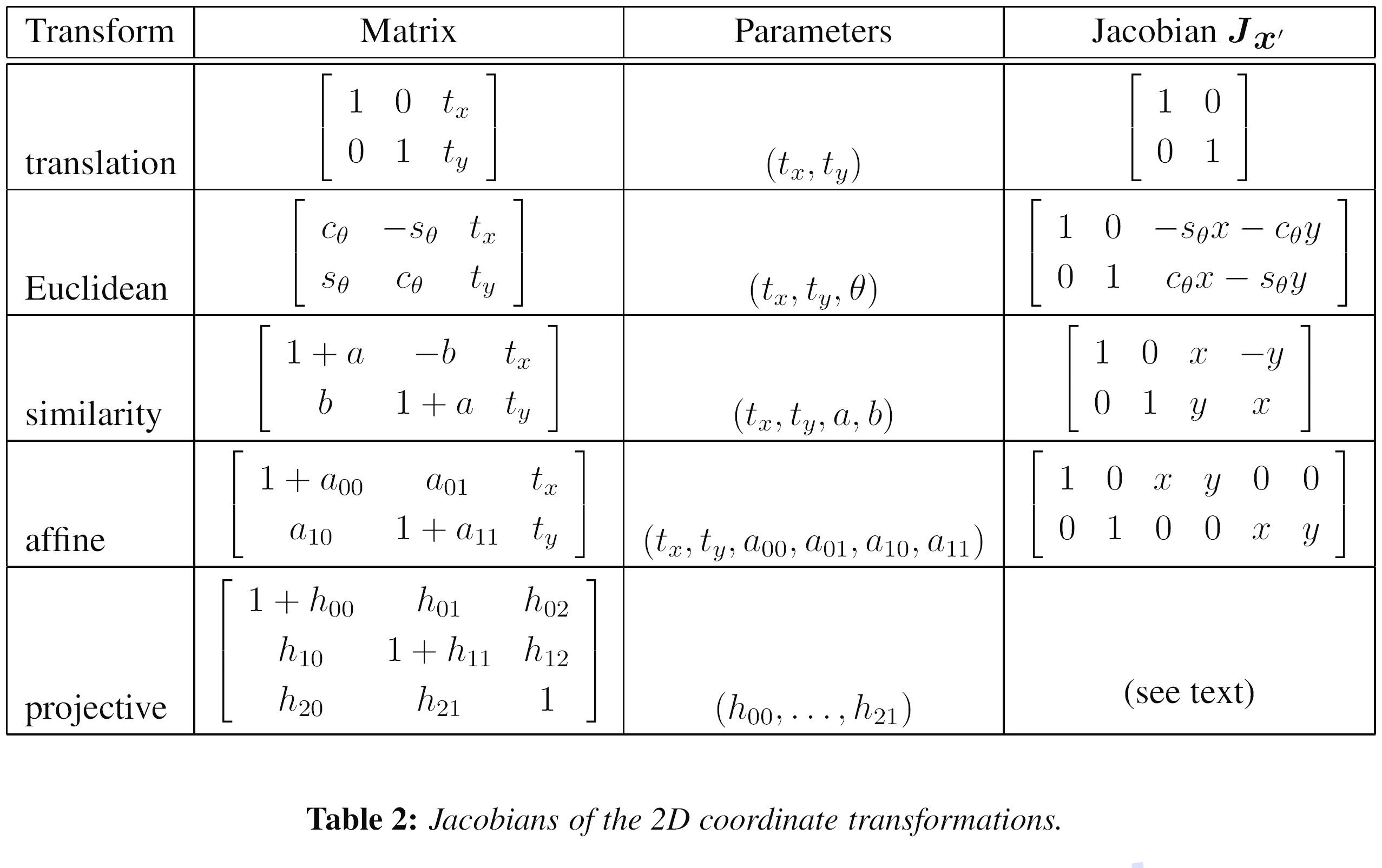
表2：二维坐标转换的雅可比行列式。

表2显示了在§2中引入的2D平面变换的运动雅可比矩阵J_x'。¹⁵ 请注意，我如何重新参数化运动矩阵，以便它们始终是原点p = 0的标识。 我们讨论合成和逆合成算法。 (这也使对动作施加先验更加容易。)

　　15在§4.3中给出了在§2.2中引入的3D旋转运动模型的导数。

表2中的导数都非常简单，除了投影的二维运动(单应性)外，它需要按像素划分才能评估，c.f (8)，在这里以新的参数形式重写为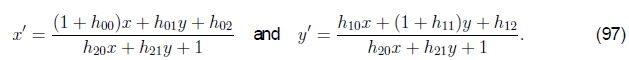

雅可比Jacobian为

其中D是(97)中的分母，它取决于当前参数设置(x'和y'也是一样)。

对于参量运动，(Gauss-Newton)Hessian和梯度加权残差矢量变为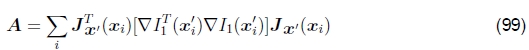

和

请注意，方括号内的表达式如何与在较简单的平移运动情况下计算出的表达式相同(82-83)。

基于补丁的近似值。与平移情况相比，用于参量运动的Hessian向量和残差向量的计算可能要昂贵得多。对于具有n个参数和N个像素的参数运动，A和b的累加需要O(n²N) 运算(Baker和Matthews 2004)。减少此数量的一种方法是将图像分成较小的子块(补丁)P_j，并仅在像素级别的方括号内累积更简单的2×2数量(Shum和Szeliski 2000)，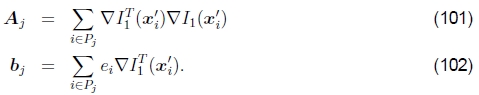

完整的Hessian和残差可以近似为

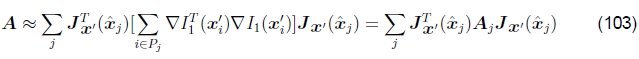
和

其中ˆx_j是每个补丁P_j的中心(Shum和Szeliski 2000)。这等效于用分段恒定近似替换真实运动Jacobian。实际上，这很好。在第4.4节中讨论了这种近似与基于特征的注册的关系。

合成方法对于单应性之类的复杂参数运动，运动雅可比行列式的计算变得很复杂，并且可能涉及每个像素的划分。Szeliski和Shum(1997)观察到，这可以通过根据当前运动估计x'(x; p)首先对目标图像进行变形来简化，

然后将此变形图像与模板I₀(x)进行比较，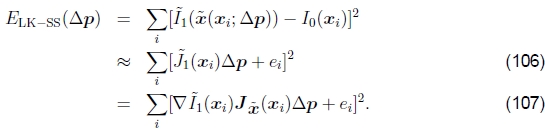

请注意，由于假定这两个图像相当相似，因此仅需要增量参数运动，即可以围绕p=0评估增量运动，这可能导致相当大的简化。例如，平面投影变换(97)的雅可比行列式变为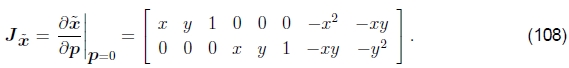

一旦计算了增量运动˜x，它就可以放在先前估计的运动之前，这对于以变换矩阵表示的运动(例如表1和2中给出的运动)很容易做到。Baker和Matthews(2004)将此称为前向合成算法，因为目标图像正在重新变形，并且最终运动估计值正在合成。

如果扭曲的图像和模板图像的外观足够相似，则可以用I₀(x)的梯度替换〜I₁(x)的梯度，如先前在(85)中建议的那样。 这具有潜在的巨大优势，因为它允许对(99)中给出的Hessian矩阵A进行预计算(和反演)。 残差向量b(100)也可以被部分地预先计算，即，最陡的下降图像∇I₀(x)J_〜x(x)可以被预先计算并存储以用于以后与e(x)=〜I₁(x)-I₀(x)的乘法错误图片(Baker and Matthews 2004)。 这个想法最初是由Hager和Belhumeur(1998)在Baker和Matthews(2004)所谓的正向加性方案中提出的。

贝克和马修斯(Baker and Matthews，2004)引入了另一种变体，称为反成分算法。他们没有(从概念上)重新扭曲变形的目标图像〜I₁(x)，而是扭曲了模板图像I₀(x)并最小化了

这与前向翘曲算法(107)相同，除了e_i的符号以外，用梯度∇I₀(x)代替了梯度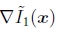。 所得的更新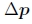是由修改项(107)计算的更新的负数，因此，增量变换的逆必须先于当前变换。 因为逆合成算法有可能预先计算逆黑森州和最陡的下降图像，这使其成为(Baker and Matthews 2004)中所调查者的首选方法。 摘自(Baker等人2003a)的图12精美地显示了实现逆合成算法所需的所有步骤。

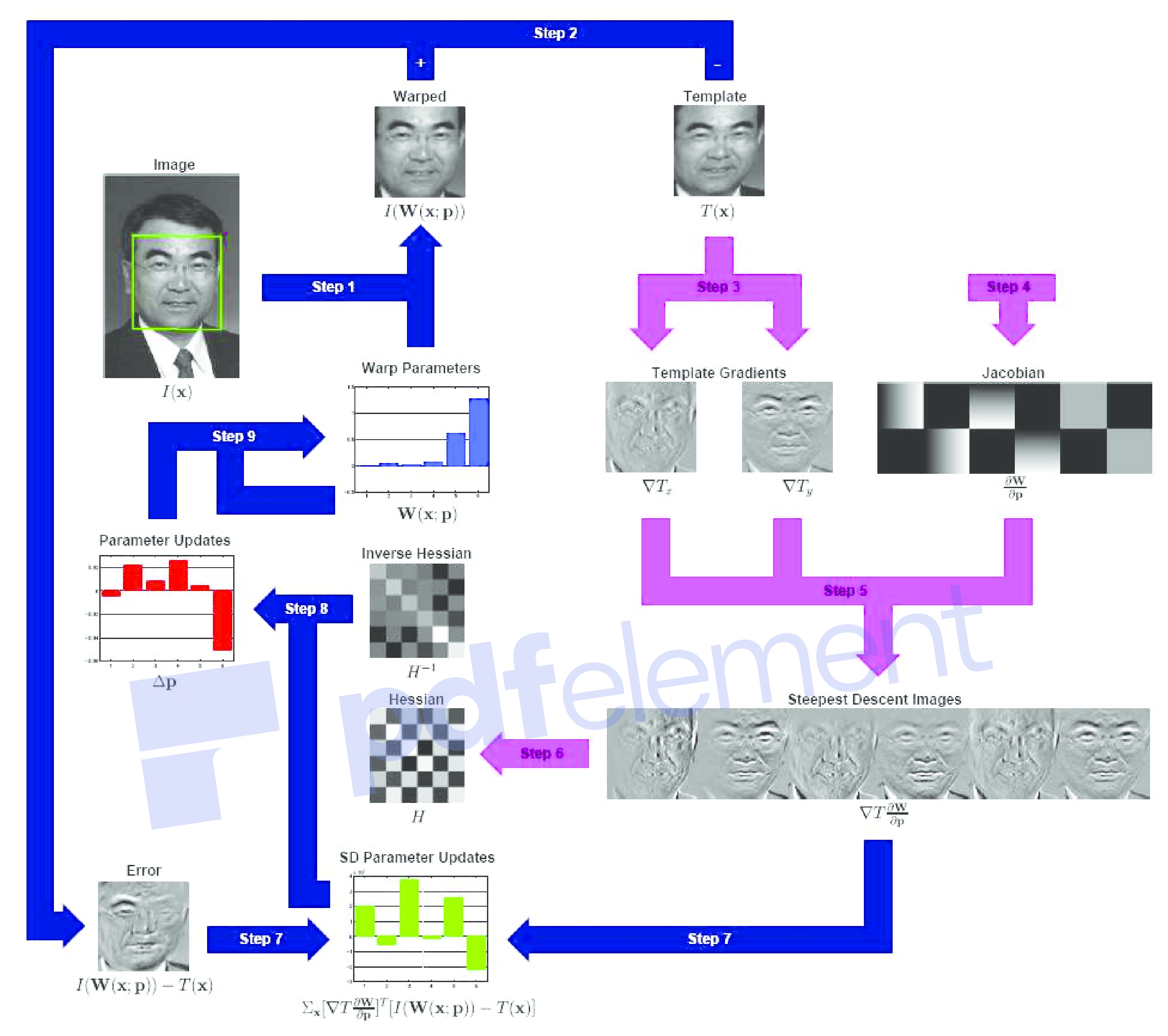
图12：逆合成算法的示意图(经许可，从(Baker等，2003a)复制)。步骤3-6(浅色箭头)作为预计算执行一次。主要算法仅包含以下迭代：图像变形(步骤1)，图像差分(步骤2)，图像点积(步骤7)，与Hessian逆的乘法(步骤8)以及对变形的更新(步骤9)。)。所有这些步骤都可以高效执行。

Baker和Matthews(2004)还讨论了使用高斯-牛顿迭代(即最小二乘的一阶展开，如上所述)与其他方法(例如最速下降法和Levenberg-Marquardt)的优势。该系列的后续部分(Baker等人2003a，Baker等人2003b，Baker等人2004)讨论了更高级的主题，例如每像素权重，提高效率的像素选择，对稳健指标的更深入讨论以及算法，线性外观变化以及参数先验。它们为有兴趣实施增量图像配准的高度优化实现的任何人提供了宝贵的阅读资源。

4基于特征的注册

如前所述，直接匹配像素强度只是图像配准的一种可能方法。另一个主要方法是首先从每幅图像中提取独特的特征，以匹配这些特征以建立全局对应关系，然后估计图像之间的几何变换。这种方法自立体匹配的早期(Hannah 1974，Moravec 1983，Hannah 1988)就被使用，并且最近在图像拼接应用中也越来越流行(Zoghlami等人，1997； Capel和Zisserman，1998； Cham和Cipolla，1998)。 Badra等人，1998； McLauchlan和Jaenicke，2002； Brown和Lowe，2003； Brown等人，2005)。

在本节中，我将介绍检测独特点，进行匹配以及计算图像配准的方法，包括第2.2节中介绍的3D旋转模型。 我还将讨论直接和基于功能的方法的相对优缺点。 

4.1关键点检测器

正如我们在§3.4中所看到的那样，运动估计的可靠性最关键地取决于图像Hessian矩阵最小特征值λ₀(Anandan 1989)的大小。这使其成为寻找图像中可以高精度匹配的点的合理候选者。 (该领域中的较旧术语讨论了“角状”特征(Moravec 1983)，但是现代用法是关键点，兴趣点或显着点。)确实，Shi和Tomasi(1994)提出使用此数量来发现良好特征。跟踪，然后结合使用平移和基于细微的斑块比对，以通过图像序列跟踪此类点。

使用权重相等的方形补丁可能不是最佳选择。相反，可以使用高斯加权函数。Förstner(1986)和Harris and Stephens(1988)都提出了使用这种方法发现关键点的建议。可以使用一系列滤波器和代数运算来有效评估Hessian和特征值图像，

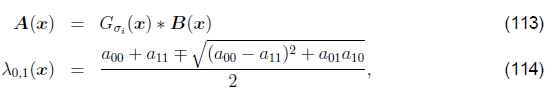
其中G_σd是宽度为σ_d的降噪预平滑“导数”滤波器，G_σi是积分滤波器，其比例为σ_i，用于控制有效补丁大小。 (a_ij是A(x)矩阵中的条目，为简洁起见，我在其中删除了(x)。)例如，Förstner(1994)使用σ_d=0.7和σ_i=2。一旦计算出最小特征值图像，就可以找到局部最大值作为潜在的关键点。

最小特征值不是唯一可用于发现关键点的数量。哈里斯和斯蒂芬斯(1988)提出的一个更简单的量是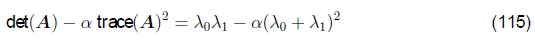

与α=0.06。 Triggs(2004)建议使用数量

(例如α= 0.05)，这会降低一维边缘的响应，其中混叠误差有时会影响较小的特征值。 他还展示了如何将基本的2×2 Hessian扩展到参数运动，以检测在比例和旋转上也可以精确定位的点。 布朗等人(2005)，另一方面，使用调和均值，

在λ₀≈λ₁所在的区域中，这是更平滑的功能。图13显示了各种兴趣点算子的等高线(请注意，所有检测器都需要两个特征值都较大)。图14显示了Brown等人的多尺度定向斑块检测器的输出。 (2005)在5种不同的规模上。

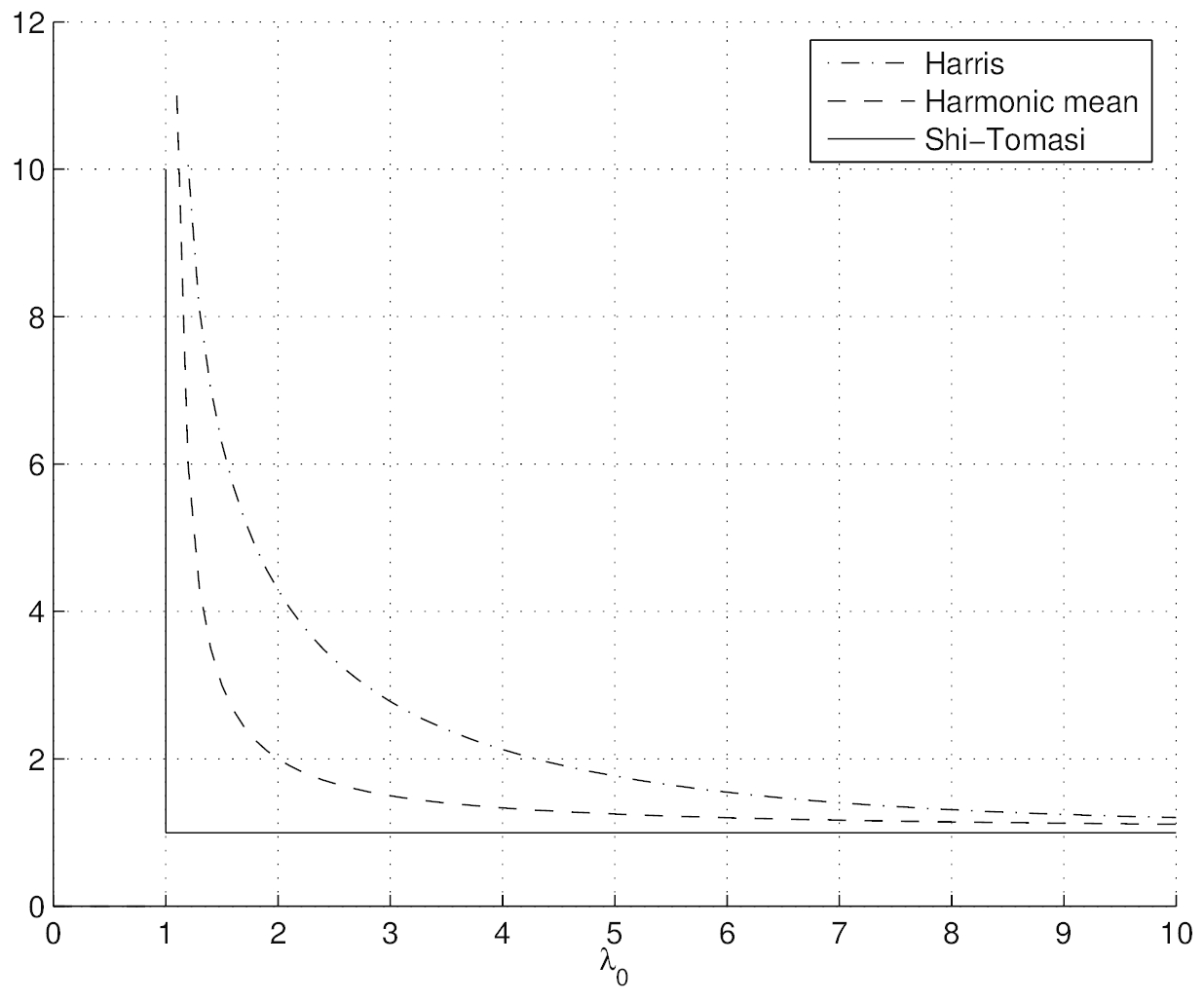
图13：流行的关键点检测功能的等高线图(摘自(Brown等，2004)。 每个检测器寻找的特征值λ₀、λ₁都较大的点。

图14：在五个金字塔级别提取的多尺度定向补丁(MOPS)(摘自(Brown等人，2004年))。这些框显示了特征方向和从中采样描述符向量的区域。

Schmid等人(2000年)调查了大量关于关键点检测的文献，并进行了一些实验比较以确定特征检测器的可重复性，这被定义为在扭曲图像中相应位置的ε=1.5像素内发现一幅图像中检测到关键点的频率。他们还测量每个检测到的特征点上可用的信息内容，它们定义为一组旋转不变的局部灰度描述符的熵。在他们调查的技术中，他们发现带有σ_d=1和σ_i=2的Harris算子的改进版本效果最好。

最近，有人提出了尺度不变的特征检测器(Lowe 2004，Mikolajczyk和Schmid 2004)和仿射变换(Baumberg 2000，Kadir和Brady 2001，Schaffalitzky和Zisserman 2002，Mikolajczyk等人2005)。当匹配具有不同比例或方面的图像时(例如用于3D对象识别)，这些功能非常有用。一种实现尺度不变性的简单方法是寻找在亚八度金字塔上计算出的高斯差(DoG)(Lindeberg 1990，Lowe 2004)或Harris角(Mikolajczyk and Schmid 2004，Triggs 2004)探测器的尺度空间最大值，即，一个图像金字塔，其中相邻级别之间的子采样小于两倍。洛(Lowe)的原始论文(2004)使用半八度音阶octave(√2)金字塔，而特里格斯(Triggs(2004))建议使用四分之一八度音阶octave(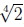)。特征点检测器和描述符的领域仍然非常活跃，每年在大型计算机视觉会议上发表论文(Carneiro和Jepson 2005，Kenney等2005，Bay等2006，Platel等2006，Rosten和Drummond，2006年)，请参见Mikolajczyk等人最近对仿射区域探测器的调查和比较。 (2005)。

当然，关键点不是唯一可用于注册图像的功能。Zoghlami等人(1997年)使用线段以及点状特征来估计成对图像之间的单应性，而(Bartoli等人2004年)使用沿边缘具有局部对应关系的线段来提取3D结构和运动。Tuytelaars和Van Gool(2004)使用细微不变的区域来检测宽基线立体匹配的对应关系。Matas等(2004)使用与流域检测有关的算法来检测最大稳定区域，而局部最大。 (Corso和Hager(2005)使用一种相关技术将面向2D的高斯核拟合到均匀区域。)虽然这些技术都可以用来解决图像配准问题，但本调查将不对其进行详细介绍。

4.2特征匹配

 在检测到特征(关键点)之后，我们必须对它们进行匹配，即确定哪些特征来自不同图像中的相应位置。在某些情况下，例如，对于视频序列(Shi和Tomasi，1994年)或已被纠正的立体声对(Loop和Zhang，1999年，Scharstein和Szeliski，2002年)，每个特征点周围的局部运动可能大部分是平移的。在这种情况下，第3.1节中引入的误差度量(例如E_SSD或E_NCC)可用于直接比较每个特征点周围小补丁中的强度。 (下面讨论的Mikolajczyk和Schmid(2005)的比较研究使用互相关。)由于可能无法精确定位特征点，因此可以通过执行第3.4节中所述的增量运动修正来计算更准确的匹配分数。耗时，有时甚至会降低性能(Brown等人，2005)。

如果在较长的图像序列上跟踪特征，则它们的外观可能会发生较大的变化。 在这种情况下，使用仿射运动模型比较外观是有意义的。 Shi和Tomasi(1994)使用转换模型在相邻帧之间比较补丁，然后使用此步骤产生的位置估计值来初始化当前帧中的补丁与首次检测到特征的基础帧之间的仿射配准。 实际上，特征很少被检测到，即仅在跟踪失败的区域中被检测到。 在通常情况下，使用增量配准算法搜索特征当前预测位置周围的区域。 这种算法是先检测后跟踪的方法，因为检测很少发生。 适用于可以合理预测特征点的预期位置的视频序列。

对于较大的运动，或对于图像之间的几何关系未知的匹配图像集合(Schaffalitzky和Zisserman 2002，Brown和Lowe 2003)，首先在所有图像中都检测到特征点的先检测后匹配方法更为合适。因为特征可以以不同的方向或比例出现，所以必须使用更多的视图不变类型的表示形式。Mikolajczyk和Schmid(2005)回顾了一些最近开发的视图不变的局部图像描述符，并通过实验比较了它们的性能。

补偿平面内旋转的最简单方法是在对补丁进行采样或计算描述符之前，在每个特征点位置找到主导方向。布朗等人(2005)使用平均梯度方向的方向，该方向是在每个特征点的较小邻域内计算的，而Lowe(2004)(以及Mikolajczyk和Schmid不变)仅通过选择尺度空间中局部最大值的特征点来进行尺度缩放，如第4.1节所述。使描述符对于细微的变形(拉伸，挤压，偏斜)保持不变甚至更加困难(Baumberg，2000； Schaffalitzky和Zisserman，2002)。Mikolajczyk和Schmid(2004)使用特征点周围的局部第二矩矩阵来定义规范框架，而Corso和Hager(2005)将二维定向的高斯核拟合到均匀区域并存储加权区域统计信息。

在Mikolajczyk和Schmid(2005)比较的局部描述符中，他们发现David Lowe(2004)的尺度不变特征变换(SIFT)通常表现最好，其次是Freeman和Adelson(1991)的可操纵滤波器，然后是互相关的(可以通过逐步改善位置和姿势来改善这种状况，但请参见(Brown等人，2005年)。微分不变量的描述符对设计导致的方向变化不敏感，因此效果也不理想。

SIFT特征是通过使用局部梯度方向的直方图首先估计局部方向来计算的，它可能比平均方向更准确。一旦建立了局部框架，就将渐变复制到不同的定向平面中，并将这些图像的模糊重采样版本用作特征。这为描述符提供了对小特征定位误差和几何变形的不敏感(Lowe 2004)。

可控滤波器是高斯滤波器导数的组合，可以快速计算所有可能方向上的偶数和奇数(对称和反对称)边缘状和角状特征(Freeman和Adelson 1991)。因为它们使用的是广义的高斯函数，所以它们对定位和方向误差也不敏感。

对于不显示大量缩图的任务，例如图像拼接，简单的归一化强度补丁表现相当好，并且易于实现(Brown等人，2005年)(图15)。 特征描述符领域继续快速发展，获得了更新的结果，包括SIFT特征描述符的主成分分析(PCA)(Ke和Sukthankar 2004)和包括局部颜色信息的描述符(van de Weijer和Schmid 2006)。

图15：使用偏置/增益归一化强度值的8 × 8采样形成MOP描述符，相对于检测尺度，采样间隔为5个像素(摘自(Brown等人2004))。这种低频采样使特征对关键点位置误差具有一定的鲁棒性，并且可以通过在比检测尺度更高的金字塔层次上采样来实现。

快速索引和匹配。查找图像对中所有对应特征点的最简单方法是使用上述局部描述符之一将一个图像中的所有特征与另一图像中的所有特征进行比较。不幸的是，这在预期的功能数量上是二次的，这对于某些应用程序来说是不切实际的。

可以使用不同类型的索引方案来设计更有效的匹配算法，其中许多都是基于在高维空间中找到最近的邻居的想法。例如，Nene and Nayar(1997)开发了一种他们称为切片的技术，该技术使用一系列1D二进制搜索来有效地剔除位于查询点超立方体内的候选点列表。他们还很好地回顾了该领域以前的工作，包括诸如k-d树之类的空间数据结构(Samet 1989)。Beis和Lowe(1997)提出了一种Best-Bin-First(BBF)算法，该算法对k-d树算法使用了一种经过修改的搜索顺序，以便按距查询位置最近的距离搜索特征空间中的bin。Shakhnarovich等(2003年)扩展了以前开发的称为位置敏感哈希的技术，该技术使用独立计算的哈希函数的并集，使其对参数空间中点的分布更加敏感，他们称之为参数敏感哈希。布朗等(2005年)从8*8图像补丁中散列了第三个(非恒定)Haar小波。甚至最近，Nister和Stewenius(2006)使用了度量树，该树包括将特征描述符与层次结构中每个级别的少量原型进行比较。 尽管进行了所有有希望的工作，但是快速计算图像特征对应关系远非解决问题。

RANSAC和LMS。一旦计算出一组初始的特征对应关系，我们需要找到一个将产生高精度对准的集合。一种可能的方法是简单地计算最小二乘估计值，或使用最小二乘的稳健(迭代重新加权)版本，如下所述(第4.3节)。但是，在许多情况下，最好先找到一个良好的初始内联点集，即所有与某个特定运动估计值一致的点。¹⁶

　　16对于直接估计方法，通常使用分级(粗到精)技术来锁定场景中的主导运动(Bergen等人，1992a，Bergen等人，1992b)。

解决此问题的两种广泛使用的解决方案称为RANdom SAmple Consensus，或简称RANSAC(Fischler和Bolles 1981)和最小二乘平方中位数(LMS)(Rousseeuw 1984)。 两种技术都始于(随机地)选择k个对应项的子集，然后将其用于计算运动估计p，如第4.3节所述。 然后，将全套对应项的残差计算为

其中〜x'_i是估计(映射)位置，而x'_i是感测(检测)特征点位置。

然后，RANSAC技术计算在其预测位置的1/3之内(即其)的内部数量。 (The值取决于应用程序，但通常约为1-3个像素。)最小二乘方中值可得出||r_i||值的中值。

重复随机选择过程S次，并保留具有最多内部数(或中位数残差最小)的样本集作为最终解决方案。然后，将初始参数猜测值p或计算出的所有惯常值集传递给下一个数据拟合阶段。在最近开发的RANSAC版本中，称为PROSAC(渐进式样本一致)，首先从最“一致”的匹配中添加随机样本，从而加快了(统计上)可能的良好内在集的查找过程(Chum和Matas 2005)。 )。

了确保随机抽样有很好的机会找到一组真实的内线，必须尝试足够数量的试验S。设p为任何给定对应关系有效的概率，P为S次试验后成功的总概率。在一个试验中，所有k个随机样本都是内部值的可能性是p^k。因此，S种此类试验都将失败的可能性是

所需的最少试验次数为

Stewart(1999)给出了以下示例，这些示例要求达到99％的成功概率所需的试验次数S：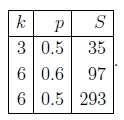

如您所见，随着使用的采样点数量的增加，试验的数量迅速增加。 这为在任何给定的试验中使用尽可能少的采样点k提供了强烈的动力，这实际上是通常使用RANSAC的方式。


4.3几何配准

一旦我们计算出一组匹配的特征点对应关系，下一步就是估计最能记录两个图像的运动参数p。通常的方法是使用最小二乘，即最小化由(118)，

第2节中介绍的许多运动模型，即平移，相似性和相似性，在运动和未知参数之间具有线性关系p.¹⁷在这种情况下，使用正态方程Ap = b的简单线性回归(最小二乘)效果很好。

　　17 可以通过线性算法估算二维欧几里德运动，方法是先独立估计余弦和正弦项，然后对其进行归一化以使其大小为1。

不确定度加权和稳健回归。上面的最小二乘公式假定所有特征点都以相同的精度匹配。通常不是这种情况，因为某些点可能会落在比其他点更多的纹理区域中。如果我们将方差估计值σ_i²与每个对应关系相关联，那么我们可以最小化加权最小二乘，

如第3.4节所述，可以通过将Hessian的倒数与每个像素的噪声估算值相乘来获得基于补丁的匹配的协方差估算值(86)。通过逆方差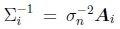(称为信息矩阵)对每个平方残差进行加权，得到

其中A_i是黑森补丁(101)。

如果在基于特征的对应关系中存在异常值(并且几乎总是存在)，则最好使用最小二乘的可靠版本，即使已使用初始RANSAC或MLS阶段来选择合理的线性值也是如此。然后，将健壮的最小二乘成本度量(类似于(45))

如前所述，一种最小化此数量的常用方法是使用迭代重新加权的最小二乘，如第3.4节所述。

单应性更新。对于非线性测量方程式，例如(97)中的单应性，此处重写为和

需要迭代解决方案才能获得准确的结果。 对8个未知数的初步猜测{h₀₀，... ，h₂₁}可以通过将等式的两边都乘以分母得出线性的等式组，

但是，从统计的角度来看，这不是最佳的，因为分母之间的差异可能会很大。

对此进行补偿的一种方法是通过对分母D的当前估计值的逆来对每个方程重新加权,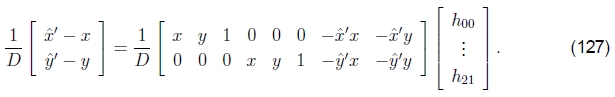

尽管这乍一看似乎与(126)完全相同，但由于使用最小二乘法求解超定方程组，因此权重确实很重要，并且会产生一组性能更好的正态方程组在实践中(带有嘈杂的数据)。

但是，最基本的估算方法是使用Gauss-Newton逼近直接最小化平方残差方程(118)，即在p中执行一阶泰勒级数展开，得到

或

虽然这看起来类似于(127)，但在两个重要方面有所不同。 首先，左手边由未加权的预测误差而不是像素位移组成，并且解矢量是对参数矢量p的扰动。 其次，J_x'内部的数量涉及预测的特征位置(〜x'，〜y')，而不是感测到的特征位置(ˆx'、ˆy')。 两者都很微妙，但是它们导致了一种算法，当与下坡步的正确检查相结合时(如在Levenberg-Marquardt算法中一样)，将收敛到最小。 (不保证对(127)式进行迭代，因为这没有使定义明确的能量函数最小化。)

上面的公式类似于直接注册的加性算法，因为要计算对完全转换的更改，请参阅§3.5。 如果我们将增量单应性放在当前的单应性之前，即使用组合算法，则D = 1(因为p = 0)，并且上述公式简化为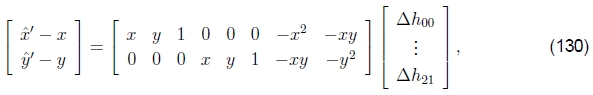

为了简洁起见，我用(x，y)替换了(〜x'，〜y')。 (请注意，这如何导致与(108)相同的雅可比行列式。)

旋转全景图更新。如第2.2节所述，使用旋转矩阵和焦距的集合表示全景图像的对齐方式会比直接使用单应性图产生更稳定的估计问题(Szeliski 1996，Szeliski和Shum 1997)。给定这种表示方式，我们如何更新旋转矩阵以最佳地对齐两个重叠的图像？

回想一下(18-19)，涉及两个视图的方程可以写成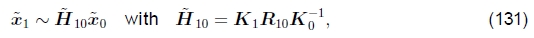

其中K_k= diag(f_k, f_k, 1) 是校准矩阵，而R₁₀ = R₁R₀^-1是两个视图之间的旋转。更新R₁₀的最佳方法是将增量旋转矩阵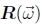附加到当前估计值R₁₀上(Szeliski和Shum，1997； Shum和Szeliski，2000)，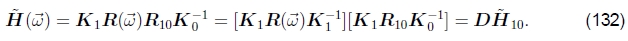

请注意，这里我以合成形式编写了更新规则，其中增量更新D优先于当前单应性。使用(26)中给出的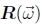的小角度近似值，我们可以将增量更新矩阵写为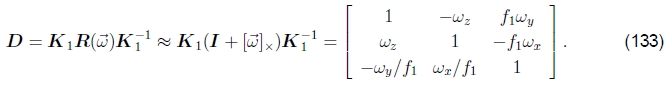

请注意，现在D矩阵中的条目与表2和(125)中使用的h₀₀，...，h₂₁参数之间存在良好的一对一对应关系，即

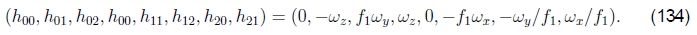
因此，我们可以将链式规则应用于(130)和(134)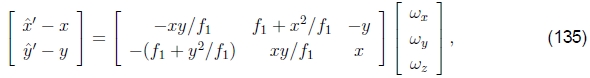

给出了估计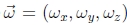所需的线性化更新方程。¹⁸请注意，此更新规则取决于目标视图的焦距f₁，并且与模板视图的焦距f₀无关 。 这是因为合成算法实质上会对目标产生较小的扰动。 一旦计算了增量旋转矢量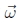，就可以使用R₁←R(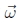)R₁ 更新R₁旋转矩阵。

　　18这与瞬时刚性流的旋转分量(Bergen等人，1992a)相同，并且与(Szeliski and Shum 1997，Shum and Szeliski 2000)中给出的更新方程式相同。

更新焦距估计值的公式要复杂得多，并在(Shum and Szeliski 2000)中给出。 我不会在这里重复它们，因为在第5.1节中将给出一个基于最小化反向投影3D射线之间差异的替代更新规则。 图16显示了3D旋转运动模型下的四个图像的对齐方式。

图16：使用3D旋转运动模型注册的手持模型拍摄的四幅图像(来自(Szeliski和Shum，1997年))。 请注意，单应性如何具有良好定义的梯形形状，而不是任意的，梯形形状的宽度远离原点增加。

焦距初始化。为了初始化3D旋转模型，我们需要同时估计摄像机的焦距和旋转矩阵的初始猜测。可以使用基于(Szeliski and Shum 1997)中首先提出的公式，从基于单应性(平面透视)的对准线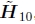直接获得。

使用(19)中使用的校准矩阵K_k= diag(f_k, f_k, 1)的简化形式，我们可以将(131)重写为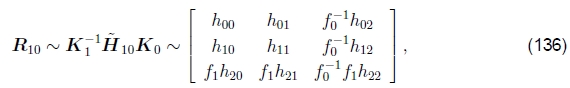

其中h_ij是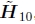的元素。

利用旋转矩阵R₁₀的正交性和(136)的右手仅在一定范围内已知的事实，我们得到

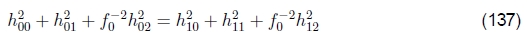
和

据此，我们可以计算出f₀的估算值

或

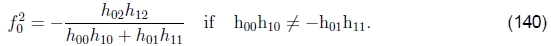
(请注意，(Szeliski和Shum 1997)中给出的方程是错误的；可以在(Shum and Szeliski 2000)中找到正确的方程。)如果以上两个条件都不成立，我们也可以取第一个(或 第二)行和第三。 通过分析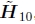的列，对于f1也可以获得类似的结果。如果两个图像的焦距相同，我们可以将f₀和f₁的几何平均值作为估计的焦距f =√(f₁f₀)。 当f的多个估计值可用时(例如，来自不同的单应性)，可以将中值用作最终估计值。

间隙闭合。 本节中介绍的技术可用于估计一系列旋转矩阵和焦距，它们可以链接在一起以创建大全景图。 不幸的是，由于累积的错误，这种方法很少会生成封闭的360度全景图。 相反，将始终存在间隙或重叠(图17)。

图17：间隙闭合：(a)当焦距错误时可见间隙(f = 510)； (b)对于正确的焦距(f = 468)，看不到任何间隙。

我们可以通过将序列中的第一个图像与最后一个图像进行匹配来解决此问题。 与该帧相关联的两个旋转矩阵估计之间的差异表示套准量。 通过获取与这些旋转相关联的两个四元数的商，然后将该“误差四元数”除以序列中图像的数量(假设帧间旋转相对恒定)，可以将该误差均匀地分布在整个序列中。 我们还可以根据未对准的数量更新估计的焦距。 为此，我们首先将误差四元数转换为间隙角θ_g。 然后，我们使用公式f'= f(1-θ_g/ 360°)更新焦距。

图17a显示了配准图像序列的结尾和第一个图像。 最后一个图像和第一个实际上是相同图像的图像之间有很大的差距。 差距为32°，因为使用了错误的焦距估计(f = 510)。 图17b显示了以正确的焦距(f = 468)缩小间隙后的定位。 请注意，两个镶嵌图都显示很少的视觉重合失调(间隙处除外)，但是图17a是使用具有9％误差的焦距计算得出的。 (Hartley 1994，McMillan and Bishop 1995，Stein 1995，Kang and Weiss 1997)开发了相关方法来解决使用纯平移运动和柱面图像的焦距估计问题。

不幸的是，这种特殊的缩小间隙的启发式方法仅适用于相机不断向同一方向旋转的“一维”全景。在下一节§5中，我将介绍一种适用于任意相机运动的消除间隙和重叠的不同方法。

4.4直接对齐与基于特征对齐

假设存在这两种对齐图像的替代方法，哪个更可取？

我曾经当过直接匹配营地的负责人(Irani和Anandan 1999)。早期基于特征的方法似乎在纹理过多或纹理不足的区域中感到困惑。这些特征通常会在图像上不均匀地分布，从而无法匹配应该对齐的图像对。此外，建立对应关系依赖于围绕特征点的面片之间的简单互相关，当图像旋转或由于单应性而缩短时，这种互相关不能很好地工作。

如今，特征检测和匹配方案非常强大，甚至可以用于从广泛分离的视图中进行已知的对象识别(Lowe 2004)。 特征不仅响应于高“拐角”区域(Förstner1986，Harris and Stephens 1988)，而且还响应“斑点状”区域(Lowe 2004)以及统一区域(Tuytelaars和Van Gool 2004)。 此外，由于它们在比例空间中操作并使用主导方向(或方向不变的描述符)，因此它们可以匹配比例，方向甚至是透视不同的图像。 我自己最近在使用基于特征的方法时的经验是，如果特征在图像上分布得很好，并且为重复性合理地设计了描述符，通常可以找到足以进行图像拼接的对应关系(Brown等人，2005年)。

我以前喜欢直接方法的另一个主要原因是，它们可以最佳利用图像对齐中可用的信息，因为它们可以测量图像中每个像素的贡献。 此外，假设高斯噪声模型(或其稳健版本)，则它们例如通过强调高梯度像素的贡献来适当地加权不同像素的贡献。 (参见Baker等人(2003a)，他们建议在强梯度上添加更多的权重是可取的，因为梯度估计中存在噪声。)有人可能会争辩说，对于仅具有缓慢变化的梯度的模糊图像，将找到一种直接方法 对齐，而特征检测器将找不到任何东西。 但是，这样的图像实际上在消费者成像中很少出现，并且使用比例空间特征意味着可以以较低的分辨率找到某些特征。

直接技术的最大缺点是它们的收敛范围有限。 即使可以在分层(粗到细)估计框架中使用它们，实际上，在重要细节开始被模糊掉之前，很难使用多于两个或三个级别的金字塔。 为了匹配视频中的顺序帧，通常可以使直接方法起作用。 但是，为了匹配基于照片的全景图中的部分重叠的图像，它们经常失败而无用。 我们较旧的图像拼接系统(Szeliski 1996，Szeliski和Shum 1997)依靠圆柱图像的基于傅立叶的相关性和运动预测来自动对齐图像，但是对于更复杂的序列，必须手动进行校正。 我们更新的系统(Brown等人，2004； Brown等人，2005)使用功能，并且在无需用户干预的情况下自动拼接全景图具有良好的成功率。

那时没有直接注册的角色吗？我相信有。一旦使用基于特征的方法对齐了一对图像，我们就可以将两个图像扭曲到一个公共参考帧，并使用基于补丁的对齐方式重新计算出更准确的估算值。请注意，在(103-104)中给出的基于补丁的近似值与直接对准之间的近似关系与在逆协方差加权的基于特征的最小二乘误差度量(123)之间如何紧密相关。

实际上，如果我们将模板图像分成多个小块，并在每个小块的中心放置一个假想的“特征点”，则这两种方法将返回完全相同的答案(假设在每种情况下都找到正确的对应关系)。 但是，要使此方法成功，我们仍然必须处理“异常值”，即由于视差(§5.2)或运动对象(§6.2)而与所选运动模型不匹配的区域。 尽管基于特征的方法可能更容易推断出异常值(特征可以归类为异常值或异常值)，但基于补丁的方法由于建立的对应关系更加密集，因此对于消除局部配准错误(视差)可能更有用。 ，正如我们在§5.2中讨论的那样。

5全球注册

 到目前为止，我已经讨论了如何使用直接和基于特征的方法以及各种运动模型来注册成对的图像。在大多数应用中，给我们提供的图像不止一对。然后的目标是找到一组全局一致的对齐参数，以最大程度地减少所有图像对之间的配准错误(Szeliski和Shum，1997； Shum和Szeliski，2000； Sawhney和Kumar，1999； Coorg和Teller，2000)。为了做到这一点，我们需要将成对匹配标准(44)，(94)和(121)扩展到一个涉及所有基于图像的姿势参数(第5.1节)的全局能量函数。一旦计算了整体对齐方式，我们通常需要执行局部调整，例如去除视差，以减少双重图像和由于局部配准错误而引起的模糊(第5.2节)。最后，如果给我们提供了一组无序的图像进行配准，则需要发现哪些图像一起形成一个或多个全景图。第5.3节介绍了全景识别的过程。

5.1捆绑包调整

注册大量图像的一种方法是一次将新图像添加到全景图中，将最新图像与集合中已有的先前图像对齐(Szeliski and Shum 1997)，并在必要时发现哪些图像。它重叠(Sawhney和Kumar，1999年)。在360°全景图的情况下，累积的误差可能会导致全景图两端之间存在间隙(或过度重叠)，可以通过使用称为间隙闭合(Szeliski)的过程拉伸所有图像的对齐方式来解决和Shum 1997)。但是，更好的选择是使用最小二乘法框架将所有图像同时对齐，以正确分配任何配准错误。

在摄影测量学领域中，同时调整大量重叠图像的姿势参数的过程称为捆绑调整(Triggs等人，1999)。在计算机视觉中，它首先从运动问题应用于一般结构(Szeliski和Kang 1994)，然后专门用于全景图像拼接(Shum和Szeliski 2000，Sawhney和Kumar 1999，Coorg和Teller 2000)。

在本节中，我将使用基于特征的方法来阐述全局对齐的问题，因为这会导致系统更简单。 可以通过将图像划分为小块并为每个小块创建虚拟特征对应关系来获得等效的直接方法(如§4.4和(Shum和Szeliski 2000)所述)，或通过将每个功能错误指标替换为每个像素指标。

考虑(121)中给出的基于特征的对齐问题，即

对于多图像对齐，不是具有成对特征对应关系{(x_i，ˆx'_i)}的单个集合，我们有n个特征的集合，第j个图像中的第i个特征点的位置由x_ij表示，其标量置信度(逆方差)由c_ij表示。¹⁹ 每个图像还具有一些相关的姿态参数。

　　19在图像j中未看到的特征的c_ij =0。我们也可以使用2×2逆协方差矩阵Σ_ij^-1代替c_ij，如(123)所示。

在本节中，我假定此姿势由旋转矩阵R_j和焦距f_j组成，尽管也可以根据单应性进行表述(Shum和Szeliski 1997，Sawhney和Kumar 1999)。 可以从(15–19)重写将3D点x_i映射到帧j中的点x_ij的方程式为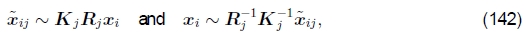

其中K_j= diag(f_k, f_k, 1)是校准矩阵的简化形式。 类似地，将帧j的点x_ij映射到帧k中的点x_ik的运动由下式给出：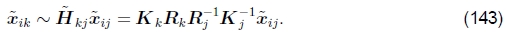

给定从成对的成对比对获得的{{R_j，f_j)}估计值的初始集合，我们如何优化这些估计值？

一种方法是将成对能量Epairwise-LS(141)直接扩展为多视图公式，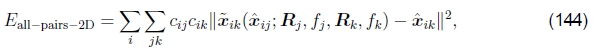

其中^〜x_ik函数是由(143)给出的帧k中特征i的预测位置，ˆx_ij是观察到的位置，下标中的“ 2D”表示图像平面误差正在最小化(Shum和Szeliski 1997 )。 注意，由于^〜x_ik取决于^〜x_ij观测值，因此我们实际上存在一个可变误差问题，从原理上讲，它需要比最小二乘方更复杂的技术来求解。 但是，实际上，如果我们有足够的特征，我们可以使用规则的非线性最小二乘法直接最小化上述数量，并获得准确的多帧对齐。²⁰

　　20虽然解决方案中总体上存在歧义，即可以将所有Rj乘以任意旋转Rg，但条件良好的非线性最小二乘算法(例如Levenberg Marquardt)将毫无问题地处理这种退化。

尽管此方法在实践中效果很好，但存在两个潜在的缺点。 首先，由于对具有相应特征的所有对进行求和，因此多次观察到的特征在最终解决方案中会变得过重。 (实际上，将m次观察到的特征计算为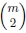次而不是m次。)其次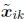， w.r.t.的导数{(R_j，f_j)}有点麻烦，尽管使用对§2.2中引入的Rj进行增量校正使此问题变得更容易处理。

制定优化方案的另一种方法是使用真正的包调整，即，不仅要求解姿态参数数{(R_j，f_j)}，还要求解3D点位置{x_i}，

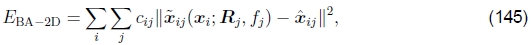
其中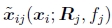由(142)给出。 完全束调整的缺点是要解决的变量更多，因此每次迭代和整体收敛都可能较慢。 (想象一下，每次更新一些旋转矩阵时3D点需要如何“移动”。)但是，可以使用稀疏矩阵技术来降低每个线性化的Gauss-Newton步骤的计算复杂度(Szeliski和Kang 1994； Hartley和Zisserman 2000； Triggs等人，1999)。

另一种替代方法是使3D投影射线方向的误差最小化(Shum and Szeliski 2000)，即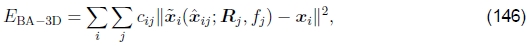

其中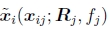由(142)的后一半给出。 与(145)相比，它本身没有特别的优势。 实际上，由于在3D射线空间中将误差最小化，因此存在着一种偏向于估计更长的焦距，因为射线之间的角度随着f 的增加而变小。

但是，如果消除3D射线x_i，我们可以导出在3D射线空间中形成的成对能量(Shum and Szeliski 2000)，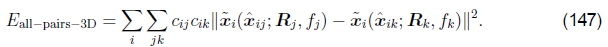

这导致更新方程组最简单(Shum和Szeliski 2000)，因为可以将f_k 折叠成均质坐标矢量的生成，如(21)所示。 因此，即使该公式使出现的特征超重了，它还是Shum和Szeliski(2000)以及我们当前的工作中使用的方法(Brown et al。2005)。 为了减少对更长焦距的偏见，我将每个残差(3D误差)乘以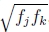，这类似于将3D射线投射到中等焦距的“虚拟相机”中，并且在实践中效果很好。

向上矢量选择。如上所述，通过上述方法计算出的3D相机的姿势存在全局歧义。尽管这似乎无关紧要，但人们还是希望最终缝合的图像“直立”，而不是扭曲或倾斜。更具体地说，人们习惯于观看显示的照片，以使垂直(重力)轴指向图像中的正上方。考虑一下平时如何拍摄照片：尽管可以以任何方式平移和倾斜相机，但通常使垂直场景线与图像的垂直边缘平行。换句话说，相机的水平边缘(X轴)通常保持平行于地面(垂直于世界重力方向)。

在数学上，对旋转矩阵的这种约束可以表示如下。回顾(142)，3D→2D投影由

我们希望将每个旋转矩阵R_k与全局旋转R_g相乘，以使全局y轴的投影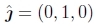垂直于图像x轴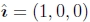.²¹

　　21请注意，这里我们使用计算机图形学中的通用约定，即垂直世界轴对应于y。 如果我们希望将与水平拍摄的“常规”图像相关的旋转矩阵作为标识，而不是绕x轴旋转90°，则这是自然的选择。

这个约束可以写成

(请注意，此处不需通过校准矩阵进行缩放)。 这等效于要求R_k的第一行垂直于R_g的第二列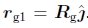。 这组约束(每个输入图像一个约束)可以写成最小二乘问题，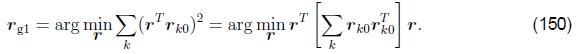

因此，r_g1是散点或矩矩阵的最小特征向量，该散点或矩矩阵由各个摄像机旋转x矢量组成，当摄像机直立放置时，通常应采用(c，0，s)的形式。

要完全指定R_g全局旋转，我们需要指定一个附加约束。 这与第6.1节中讨论的视图选择问题有关。 一种简单的启发式方法是偏向于各个旋转矩阵的平均z轴接近世界z轴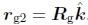。 因此，我们可以通过三个步骤来计算完整的旋转矩阵R_g：

eigenvector 特征向量

5.2视差消除

一旦我们优化了相机的整体方向和焦距，我们可能会发现图像仍未完全对准，即，合成后的缝合图像在某些地方看起来模糊或重影。这可能是由多种因素引起的，包括未建模的径向失真，3D视差(无法使相机绕其光学中心旋转)，小场景动作(如挥舞着树枝)和大范围场景动作(如人们进出图片)。
这些问题中的每一个都可以用不同的方法来处理。可以使用第2.4节中讨论的一种技术来估计径向失真(可能在第一次使用相机之前)。例如，铅垂线方法(Brown 1971，Kang 2001，El-Melegy和Farag 2003)调整径向变形参数，直到稍微弯曲的线变为直线为止，而基于镶嵌的方法调整它们，直到减少图像重叠区域中的配准误差为止( Stein(1997)，Sawhney和Kumar(1999)。

可以通过进行完整的3D束调整来攻击3D视差，即用(15)代替(145)中使用的投影方程(142)，该投影方程对相机平移进行建模。 匹配的特征点和摄像机的3D位置可以同时恢复，尽管与无视差的图像配准相比，这可能会贵得多。 一旦恢复了3D结构，就可以(理论上)将场景投影到不包含视差的单个(中央)视点。 但是，为此，需要执行密集的立体声对应(Kumar等人，1995； Szeliski和Kang，1995； Scharstein和Szeliski，2002)，如果图像仅包含部分重叠，则可能无法实现。 在这种情况下，可能仅需要在重叠区域校正视差，这可以使用多视角平面扫描(MPPS)算法来实现(Kang等人，2004； Uyttendaele等人，2004)。

当场景中的运动非常大时，即当物体完全消失时，明智的解决方案是一次仅从一张图像中选择像素作为最终合成的来源(Milgram 1977，Davis 1998，Agarwala等) (2004年)(如第6.2节所述)。 但是，当运动相当小(几个像素的数量级)时，可以使用称为局部对齐的过程(Shum和Szeliski 2000， Kang等人，2003)。 尽管它使用的运动模型比显式地对误差源建模的模型要弱，但该过程也可用于补偿径向变形和3D视差，因此可能会更频繁地失败或引入不必要的变形。

Shum和Szeliski(2000)引入的局部对齐技术始于用于优化相机姿态的全局束调整(147)。 一旦估算出这些位置，就可以将3D点xi的所需位置估算为反投影3D位置的平均值，

可以将其投影到每个图像j中以获得目标位置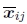。 目标位置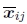与原始特征x_ij之间的差异提供了一组局部运动估计

可以插值以形成密集的校正字段u_j(x_j)。 Shum和Szeliski(2000)在他们的系统中使用反翘曲算法，将稀疏的-u_ij值放置在新的目标位置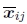上，使用双线性核函数进行内插(Nielson 1993)，然后在计算像素时将其添加到原始像素坐标中。 图像变形(校正)。 为了获得合理密集的特征集进行插值，Shum和Szeliski(2000)将特征点放置在每个面片的中心(面片的大小控制局部对齐阶段的平滑度)，而不是依赖于使用 利益经营者。

Kang等人提出了一种基于运动的去鬼影的替代方法。 (2003)，他们估计了每个输入图像和中央参考图像之间的密集光流。 在确定给定的扭曲像素有效之前，使用光一致性测度检查流矢量的准确性，并因此将其用于计算高动态范围辐射率估算值，这是其总体算法的目标。 具有参考图像的要求使其方法不太适用于一般图像拼接，尽管可以肯定地设想了这种情况的扩展。

5.3识别全景图

执行全自动图像拼接所需的最后一块是一种识别哪些图像实际组合在一起的技术，Brown和Lowe(2003)称之为识别全景图。 如果用户按顺序拍摄图像，以便每个图像与其前身重叠，并且还指定要拼接的第一个和最后一个图像，则可以使用捆绑调整与拓扑推断过程相结合来自动组装全景图(Sawhney和Kumar，1999年)。 但是，用户在拍摄全景图时经常会四处走动，例如，他们可能在上一个全景图的顶部开始新的一行，或者跳回以进行重复拍摄，或者创建360°全景图，其中需要发现端到端的重叠 。 此外，发现用户在较长时间内拍摄的多张全景图的能力可能会带来很大的便利。

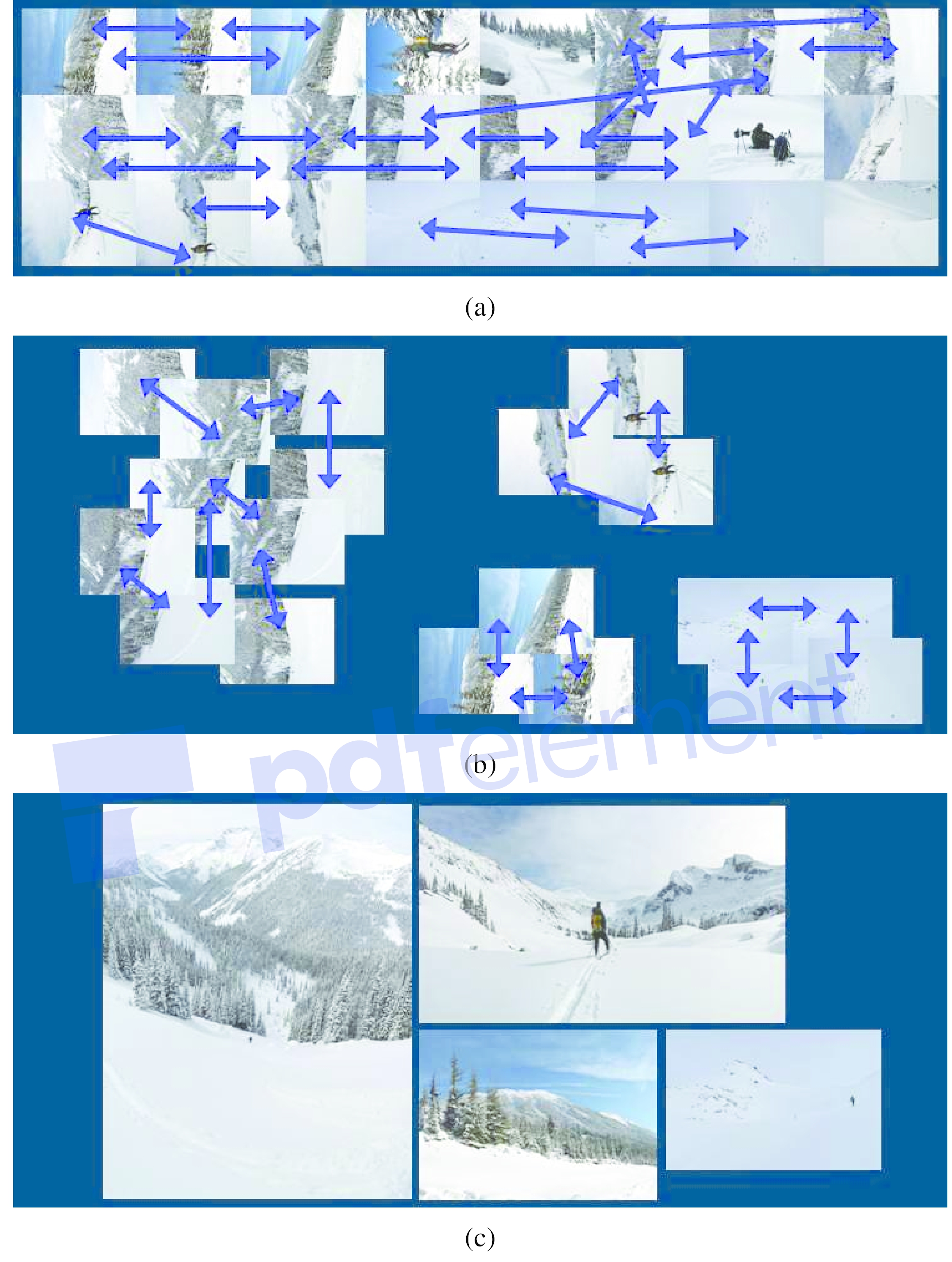
图18：使用我们的新算法识别全景图(Brown等，2004)：(a)输入图像成对匹配； (b)将图像分组为相连的成分(全景)； (c)已注册并融合到缝合合成物中的单个全景图。

图19：匹配错误(Brown等，2004)：多个特征的意外匹配会导致实际上不重叠的图像对之间的匹配。

图20：当场景包含运动对象时，通过直接像素误差比较进行的图像匹配验证可能会失败。

为了识别全景图，Brown和Lowe(2003)首先使用基于特征的方法找到所有成对的图像重叠，然后在重叠图中找到连接的组件以“识别”单个全景图(图18)。 基于特征的匹配阶段首先从所有输入图像中提取SIFT特征位置和特征描述符(Lowe 2004)，然后将它们放置在索引结构中，如第4.2节所述。 对于正在考虑的每个图像对，使用索引结构快速找到候选对象，然后比较特征描述符以找到最佳匹配，从而为第一幅图像中的每个特征找到最接近的匹配邻居。 然后，使用RANSAC使用一对匹配来假设一组相似性运动模型，然后使用该RANSAC查找一组内部匹配项，然后将其用于计算内部匹配项的数量。

在实践中，使全自动拼接算法起作用的最困难部分是确定哪些图像对实际上对应于场景的相同部分。 当使用基于特征的方法时，诸如窗口(图19)之类的重复结构可能导致错误匹配。 缓解此问题的一种方法是在注册图像之间执行基于像素的直接比较，以确定它们是否实际上是同一场景的不同视图。 不幸的是，如果场景中有移动的对象，则这种启发式方法可能会失败(图20)。 尽管没有完整的场景理解可以解决这个问题，但是可以通过应用特定领域的启发式方法(例如，典型摄像机运动的先验先验)以及应用于匹配验证问题的机器学习技术来进行进一步的改进。


6合成

一旦我们将所有输入图像相互注册，我们就需要决定如何产生最终的拼接(马赛克)图像。这涉及选择最终的合成表面(平坦，圆柱，球形等)并查看(参考图像)。它还涉及选择哪些像素有助于最终合成，以及如何最佳地融合这些像素以最小化可见的接缝，模糊和重影。

在本节中，我将介绍解决这些问题的技术，即合成表面参数化，像素/接缝选择，混合和曝光补偿。我的重点是解决问题的全自动方法。由于创建高质量的全景图和合成图与计算图一样是一项艺术上的努力，因此开发了各种交互式工具来辅助此过程，例如，(Agarwala等人，2004； Li等人，2004a； Rother等人， (2004年)。我不会在本文中介绍这些内容，除非它们为我们的问题提供了自动解决方案。 

6.1选择复合面

要做的第一选择是如何表示最终图像。 如果仅将几幅图像缝合在一起，那么自然的方法是选择其中一幅图像作为参考，然后将所有其他图像扭曲到参考坐标系中。 由于最终表面上的投影仍然是透视投影，因此所得的合成物有时称为平面全景图，因此直线保持笔直(这通常是理想的属性)。

但是，对于较大的视野，我们不能在不过度拉伸图像边界附近的像素的情况下保持平面表示。 (在实践中，一旦视野超过左右，平坦的全景图就会开始严重变形。)合成较大全景图的通常选择是使用圆柱(Szeliski 1994，Chen 1995)或球形(Szeliski and Shum 1997)投影，如第2.3节所述。实际上，可以使用在计算机图形学中用于环境映射的任何表面，包括一个立方体图，该立方体图代表具有一个立方体的六个正方形面的完整视域(Greene 1986，Szeliski和Shum 1997)。制图师还开发了许多替代方法来代表地球(Bugayevskiy和Snyder 1995)。

参数化的选择在某种程度上取决于应用程序，并且涉及在保持局部外观不失真(例如，使直线保持直线)与提供环境的合理均匀采样之间的权衡。根据全景图的范围自动进行选择并在制图表达之间平滑过渡是未来研究的有趣话题。

查看选择。选择输出参数化之后，我们仍然需要确定场景的哪一部分将在最终视图中居中。如上所述，对于平板复合图像，我们可以选择其中一张图像作为参考。通常，合理的选择是几何上最中心的选择。例如，对于表示为3D旋转矩阵集合的旋转全景图，我们可以选择z轴最接近平均z轴的图像(假设视场合理)。或者，我们可以使用平均z轴(或四元数，但这比较棘手)来定义参考旋转矩阵。

对于较大的(例如，圆柱或球形)全景图，如果已经对视球的一部分进行了成像，我们仍然可以使用相同的启发式方法。如果是完整的360°全景图，一个更好的选择可能是从输入序列中选择中间图像，或者有时是第一个图像，假设其中包含最感兴趣的对象。在所有这些情况下，通常非常需要用户控制最终视图。如果第5.1节中描述的“向上矢量”计算工作正常，则可以像平移图像或为最终全景图设置垂直“中心线”一样简单。

坐标转换。 一旦选择了参数化和参考视图，我们仍然需要计算输入和输出像素坐标之间的映射。

如果最终的合成表面是平坦的(例如单个平面或立方体贴图的表面)并且输入图像没有径向变形，则坐标变换就是(19)所描述的简单单应性。 通过适当设置纹理映射坐标并渲染单个四边形，可以在图形硬件中执行这种变形。

如果最终合成表面具有其他解析形式(例如，圆柱或球形)，我们需要将最终全景图中的每个像素转换为可见光线(3D点)，然后根据投影将其映射回每个图像中(并且可选的径向变形)方程式。通过预先计算一些查找表，例如将圆柱或球面坐标映射到3D坐标和/或每个像素处的径向畸变场所需的部分三角函数，可以使此过程更加有效。也可以通过在较粗的网格上计算精确的像素映射，然后对这些值进行插值来加快此过程。

当最终合成表面是纹理映射多面体时，必须使用稍微复杂一些的算法。不仅必须正确处理3D和纹理贴图坐标，而且还必须在纹理贴图中的三角形轮廓之外进行少量透支，以确保在3D渲染期间内插的纹理像素具有有效值(Szeliski和Shum 1997)。

抽样问题。尽管上述计算可以在每个输入图像中产生正确的(分数)像素地址，但我们仍然需要注意采样问题。例如，如果最终全景图的分辨率低于输入图像的分辨率，则必须对输入图像进行预过滤以避免混叠。这些问题已在图像处理和计算机图形社区中得到了广泛的研究。基本问题是要计算适当的预滤波器，该滤波器取决于源图像中相邻样本之间的距离(和排列)。图形社区开发了各种近似解决方案，例如MIP映射(Williams 1983)或椭圆加权高斯平均(Greene和Heckbert 1986)。为了获得最高的视觉质量，可能需要将高阶(例如立方)插值器与空间自适应预滤波器结合使用(Wang等人，2001)。在某些情况下，也可以使用称为超分辨率(§7)的过程来生成分辨率比输入图像高的图像。

6.2像素选择和加权

一旦将源像素映射到最终的合成表面上，我们仍然必须决定如何混合它们，以创建外观精美的全景图。 如果所有图像均已完美配准并完全曝光，这将是一个简单的问题(任何像素或组合都可以)。 但是，对于真实图像，可能会出现可见的接缝(由于曝光差异)，模糊(由于配准错误)或重影(由于移动的物体)。

创建干净，令人愉悦的全景图既需要决定使用哪些像素，又要如何加权或融合它们。 这两个阶段之间的区别不大，因为可以将按像素加权视为选择和混合的组合。 在本节中，我将讨论空间变化的权重，像素选择(接缝放置)，然后是更复杂的混合。

羽毛和中央重点。创建最终合成的最简单方法是简单地取每个像素的平均值，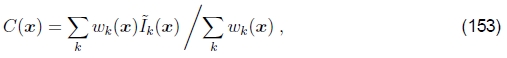

其中是变形(重新采样)的图像，w_k(x)在有效像素处为1，在其他像素处为0。 在计算机图形硬件上，这种求和可以在累积缓冲区中执行(使用A通道作为权重)。

图21：通过多种算法计算出的最终复合材料：(a)平均值，(b)中位数，(c)羽化平均值，(d)p范数p = 10，(e)Vornoi，(f)加权ROD顶点覆盖率 (g)带有Poisson混合的图形切割接缝(h)和金字塔形混合的图形。

简单平均通常效果不佳，因为曝光差异，配准错误和场景移动都非常明显(图21a)。如果快速移动的物体是唯一的问题，则通常可以使用中值滤波器(这是一种像素选择算子)将其移除(Irani和Anandan 1998)(图21b)。相反，有时可以使用中心加权(在下面讨论)和最小似然选择(Agarwala等人，2004)来保留移动物体的多个副本(图24)。

更好的平均方法是对图像中心附近的像素加权更大，而对边缘附近的像素加权更低。当图像具有一些裁切区域时，最好在裁切边缘和边缘的边缘附近降低像素的权重。这可以通过计算距离图或草拟变换来完成，

其中每个有效像素都用其到最近无效像素的欧几里德距离进行标记。欧几里得距离图可以使用两次通过栅格算法来有效地计算出来(Danielsson 1980，Borgefors 1986)。带有距离图的加权平均通常被称为羽化(Szeliski and Shum 1997，Chen and Klette 1999，Uyttendaele 等人2001)，并且可以很好地融合曝光差异。但是，模糊和重影仍然是问题(图21c)。请注意，即使将权重值(归一化为一个)，用作alpha(半透明)α通道，加权平均也不等同于使用经典的over操作(Porter和Duff 1984，Blinn 1994)对单个图像进行合成。这是因为过度操作会衰减来自更远表面的值，因此不等于直接和。

一种改善羽化的方法是将距离贴图值提高到某个较大的倍数，即使用(153)中的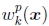。加权平均值随即成为较大值的主导，即它们的作用有点像p范数。所得的复合材料通常可以在可见的曝光差异和模糊之间提供合理的权衡(图21d)。

在极限p→∞中，仅选择权重最大的像素，

其中



是标签分配或像素选择功能，用于选择每个像素要使用的图像。 这种硬像素选择过程产生了熟悉的Vornoi图的可见性对掩模敏感的变体，该变体将每个像素分配给集合中最近的图像中心(Wood等人，1997； Peleg等人，2000)。 最终的合成物虽然可用于艺术指导和高重叠率全景照片(歧管马赛克)，但当曝光量变化时，往往具有非常硬的边缘和明显的接缝(图21e)。

Xiong和Turkowski(1998)使用这个Vornoi想法(草火变换的局部最大值)来选择接缝以进行Laplacian金字塔混合(将在下面进行讨论)。 然而，由于在添加新图像时接缝选择是顺序执行的，因此会出现一些伪像。

最佳接缝选择。计算Vornoi图是一种选择区域之间接缝的方法，在这些区域中，不同的图像会构成最终的合成。但是，Vornoi图像完全忽略了接缝下面的局部图像结构。

更好的方法是将接缝放置在图像一致的区域，以使从一个光源到另一个光源的过渡不可见。通过这种方式，该算法避免了“切穿”运动接缝看起来不自然的物体(Davis 1998)。对于一对图像，此过程可以公式化为简单的动态程序，该程序从重叠区域的一个(短)边缘开始，到另一边缘结束(Milgram 1975，Milgram 1977，Davis 1998，Efros和Freeman 2001)。

当合成多个图像时，动态程序的思想很难轻易推广。 (对于顺序合成的方形纹理瓷砖，Efros和Freeman(2001)沿着四个瓷砖侧面的每一个运行一个动态程序。)

为了克服这个问题，Uyttendaele等人。 (2001年)观察到，对于对准良好的图像，运动的物体会产生最明显的伪像，即半透明的鬼影。因此，他们的系统决定保留哪些对象以及删除哪些对象。首先，该算法比较所有重叠的输入图像对，以确定图像不一致的差异区域(ROD)。接下来，用ROD作为顶点构造图，并且边表示在最终复合图中重叠的ROD对(图22)。由于边缘的存在指示存在分歧的区域，因此必须从最终复合材料中移除顶点(区域)，直到没有边缘跨越一对剩余的顶点为止。可以使用顶点覆盖算法来计算最小的此类集合。由于可能存在多个这样的覆盖，因此使用加权的顶点覆盖来代替，其中顶点权重是通过将ROD中的羽毛权重求和来计算的(Uyttendaele等人，2001)。因此，该算法更喜欢删除图像边缘附近的区域，这样可以减少部分可见的对象出现在最终合成图像中的可能性。 (还可以通过ROD边界上的“边缘”(像素差异)来推断差异区域中的哪个对象是前景对象，当存在对象时，该值应该更高(Herley 2005)。)多余的差异区域已被删除，最终的复合材料可以使用羽毛状的混合物制成(图21f)。

图22：差异区域(ROD)的计算：(a)具有活动面的三个重叠图像； (b)相应的ROD； (c)一致ROD的图表。 (摘自(Uyttendaele et al.2001))。

Agarwala等人最近提出了一种不同的像素选择和接缝放置方法。 (2004)。 他们的系统计算标签分配，以优化两个目标函数之和。 第一个是每个像素的图像目标，它确定哪些像素可能产生良好的合成，

其中D_l(x)(x)是与在像素x处选择图像l 相关的数据损失。 在他们的系统中，用户可以通过在具有所需对象或外观的图像上“绘画”来选择要使用的像素，从而将D(x，l)设置为除用户选择的标签之外的所有标签l的较大值( 图23)。 可替代地，可以使用自动选择标准，例如偏好重复出现的像素的最大可能性(用于对象移除)，或不频繁出现的对象的最小可能性(用于最大的对象保留)。 使用更传统的中心加权数据项倾向于偏向于以输入图像为中心的对象(图24)。

图23：Photomontage从一组五个源图像(其中四个显示在左侧)中，快速创建了一个合成的全家福，每个人都在微笑着看着相机(右)。用户只需翻动堆栈，并使用指定的源图像目标在要添加到合成中的人员上方粗略绘制笔划。用户应用的笔触和计算区域由左侧(中间)的源图像的边框进行颜色编码。 (经许可复制自(Agarwala等，2004))。

图24：跟踪滑雪者跳跃的五张照片，这些照片缝合在一起形成无缝的复合材料。由于该算法更喜欢图像中心附近的像素，因此会保留寄宿生的多个副本。

第二个术语是接缝物镜，它惩罚相邻图像之间的标签差异，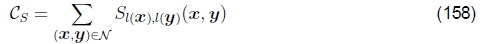

其中，S_l(x)，l(y)(x，y)是图像相关的交互代价或在像素x和y之间放置接缝的接缝成本，而N是N₄个相邻像素的集合。 例如，(Kwatra等人，2003； Agarwala等人，2004)中使用的基于颜色的简单接缝惩罚可以写为

更复杂的接缝惩罚也可以着眼于图像梯度或图像边缘的存在(Agarwala等人，2004)。 缝线罚分广泛用于其他计算机视觉应用程序中，例如立体匹配(Boykov等人，2001年)，以赋予标签功能其连贯性或平滑性。 Soille(2006)最近开发了一种替代方法，该方法使用分水岭计算沿重叠图像中的强一致边缘放置接缝。

这两个目标函数之和通常被称为马尔可夫随机场(MRF)能量，因为它是MRF分布的负对数似然性(Geman and Geman 1984)。对于一般的能量函数，发现最小值可以是NP-hard(Boykov等人，2001)。但是，这些年来，已经开发出了多种近似优化技术，包括模拟退火(Geman和Geman 1984)，图割(Boykov等2001)和循环信念传播(Sun等2003； Tappen和Freeman 2003)。 )。都Kwatra等人(2003)和Agarwala等人(2004年)使用图割，这涉及循环通过一组更简单的α扩展重标记，每种标记都可以用图割(最大流量)多项式时间算法求解(Boykov等人，2001年)。

对于图21g所示的结果，Agarwala等人。 (2004年)使用较大的数据惩罚无效像素和0为有效像素。请注意，接缝放置算法如何避免出现差异区域，包括那些与图像接壤并可能导致物体被切掉的区域。图割(Agarwala等人，2004)和顶点覆盖(Uyttendaele等人，2001)通常会产生相似的结果，尽管前者的速度明显慢，因为它可以优化所有像素，而后者对确定阈值更为敏感差异区域。

6.3混合

放置接缝并除去不需要的物体后，我们仍然需要混合图像以补偿曝光差异和其他未对准问题。先前讨论的空间变化加权(羽化)通常可以用来完成此任务。但是，在实践中很难在平滑低频曝光变化与保持足够尖锐的过渡以防止模糊之间取得令人满意的平衡(尽管使用高指数确实有帮助)。

拉普拉斯金字塔融合。 Burt和Adelson(1983)提出了解决此问题的有吸引力的方法。代替使用单个过渡宽度，而是通过创建带通(拉普拉斯)金字塔并将过渡宽度作为金字塔等级的函数来使用频率自适应宽度。该过程如下操作。

首先，将每个变形的图像转换为带通(拉普拉斯)金字塔，其中涉及使用1/16(1、4、6、4、1)二项式核对每个级别进行平滑处理，然后对平滑后的图像进行二次采样2倍。 ，然后从原始图像中减去重建的(低通)图像。 这将产生可逆的，过于完整的图像信号表示。 无效像素和边缘像素会填充有相邻值，以使此过程得到很好的定义。

接下来，将与每个源图像关联的蒙版(有效像素)图像转换为低通(高斯)金字塔。 这些模糊和欠采样的蒙版成为用于执行带通源图像的每层羽化混合的权重。

最后，通过对所有金字塔等级(带通图像)进行插值和求和来重建合成图像。 应用此金字塔混合的结果如图21i所示。

渐变域混合。多频带图像融合的另一种方法是在梯度域中执行操作。从它们的梯度场重建图像在计算机视觉中具有悠久的历史(Horn 1986)，最初是从亮度恒定性(Horn 1974)，阴影形状(Horn and Brooks 1989)和光度立体(Woodham 1981)开始的。最近，相关思想被用于从边缘重建图像(Elder和Golderg 2001)，从图像中去除阴影(Weiss 2001)，将反射与单个图像分离(Levin等人2004a)以及高动态范围的色调映射。通过减小图像边缘(梯度)的大小来获得图像(Fattal等人，2002)。

佩雷斯等人(2003年)展示了如何使用梯度域重构在图像编辑应用程序中进行无缝对象插入。而不是复制像素，而是复制新图像片段的渐变。然后，通过遵循与接缝边界处的固定Dirichlet(精确匹配)条件局部匹配梯度的泊松方程，来计算复制区域的实际像素值。佩雷斯等人(2003年)表明，这等效于计算沿边界的源图像和目标图像之间的不匹配的附加膜插值。 (众所周知，膜插值法对于任意形状的约束比频域插值法具有更好的插值特性(Nielson 1993)。)在较早的工作中，Peleg(1981)还提出增加平滑函数以沿接缝曲线强制保持一致性。

Agarwala等人 (2004年)将此想法扩展到多源公式，在这种情况下，谈论必须在接缝处精确匹配像素值的目标图像不再有意义。取而代之的是，每个源图像都贡献自己的梯度场，并使用Neumann边界条件求解泊松方程，即，删除任何涉及图像边界之外的像素的方程。

Agarwala等人而不是求解泊松偏微分方程。 (2004)直接最小化变分问题，

该方程的离散形式是一组梯度约束方程

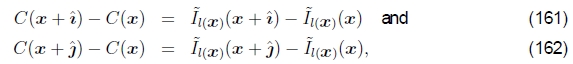
其中是x和y方向上的单位矢量。²²然后，它们解决了相关的稀疏最小二乘问题。 由于该方程组仅在加性约束条件下定义，因此Agarwala等人(2003年)提出了新的解决方案。 (2004年)要求用户选择一个像素的值。 实际上，更好的选择可能是使解决方案偏向于还原原始颜色值。

　　22在接缝位置，右侧被替换为两个源图像中的平均梯度。

为了加快这种稀疏线性系统的求解速度，(Fattal等人，2002)使用了多重网格，而(Agarwala等人，2004)则使用了分层基础的预处理共轭梯度下降法(Szeliski 1990，Szeliski 2006)。尽管在复制接缝附近的较大渐变值时要格外小心，以免引入“双边缘”，但实际上接缝融合效果很好(图21h)。

接缝放置后直接从源图像复制渐变只是渐变域融合的一种方法。 Levin等人的论文。 (2004b)研究了这种方法的几种不同的变体，他们称之为梯度域图像拼接(GIST)。他们研究的技术包括对源图像中的梯度进行羽化(融合)，以及在根据梯度场进行图像重建时使用L1范数，而不是像(160)中那样使用L2范数。他们的首选技术是对原始图像渐变(它们称为GIST1-l₁)上的羽化(混合)成本函数进行L₁优化。由于使用线性规划的L1优化可能很慢，因此他们在多网格框架中开发了更快的基于中值的迭代算法。他们的首选方法与所谓的最佳接缝(相当于Agarwala等人(2004)的方法)之间的视觉比较显示了相似的结果，同时在金字塔混合和羽化算法上有显着改进。

曝光补偿。金字塔和梯度域混合可以很好地补偿图像之间适度的曝光差异。但是，当曝光差异变大时，可能需要其他方法。

Uyttendaele等人(2001年)迭代估计每个源图像与混合合成图像之间的局部校正。 首先，在每个源图像和初始羽化合成图像之间拟合一个基于块的二次传递函数。 接下来，将传递函数与其邻居平均，以获得更平滑的映射，并通过在相邻块值之间进行样条化(插值)来计算每个像素的传递函数。 一旦对每个源图像进行了平滑调整，就可以计算出新的羽化合成，然后重复该过程(通常3次)。 (Uyttendaele et al 2001)中的结果表明，与简单的羽化相比，这种方法在曝光补偿方面做得更好，并且可以处理由于镜片渐晕等影响而导致的局部曝光变化。

高动态范围成像。 一种更基本的曝光补偿方法是从不同曝光图像估计单个高动态范围(HDR)辐射图(Mann和Picard 1995，Debevec和Malik 1997，Mitsunaga和Nayar 1999，Reinhard等人2005)。 大多数技术都假定输入图像是使用像素值固定的相机拍摄的

是将参数化辐射传递函数f(R，p)应用于比例辐射值c_kR(x)的结果。 曝光值c_k是已知的(通过实验设置，或通过相机的EXIF标签)，或作为拟合过程的一部分进行计算。

参数函数的形式因纸张而异。 Mann和Picard(1995)使用三参数f(R)=α+βR^γ 函数，Debevec和Malik(1997)使用薄板三次样条，而Mitsunaga和Nayar(1999)使用低阶(N≤ 10)多项式为传递函数的逆函数。

要将估计的(嘈杂的)辐射度值混合到最终的合成物中，Mann和Picard(1995)使用帽子函数(强调中间色调像素)，Debevec和Malik(1997)使用响应函数的导数，而Mitsunaga和Nayar (1999)优化了信噪比(SNR)，它既强调了较高的像素值，又强调了传递函数中的较大梯度。

计算出辐射度图后，通常需要将其显示在较低色域(即8位)的屏幕或打印机上。为此，已经开发了多种色调映射技术，包括计算空间变化的传递函数或减小图像梯度以适应可用的动态范围(Fattal等人，2002； Durand和Dorsey，2002； Reinhard等人，2002； Lischinski et al.2006)。

不幸的是，随意获取的图像可能无法完美对齐，并且可能包含运动物体。Kang等人(2003年)提出了一种算法，将全局配准与局部运动估计(光流)相结合，以在混合图像的辐射估计之前准确地对齐图像(图25)。由于图像的曝光可能存在很大差异，因此在生成运动估算时必须格外小心，必须自己检查其一致性，以避免产生重影和物体碎片。

图25：合并多个曝光以创建一个高动态范围的合成图像：(a–c)三种不同的曝光； (d)使用经典算法合并曝光(注意由于马的头部移动而产生的重影)； (e)将曝光与运动补偿合并(Kang等，2003)。

但是，即使相机同时进行较大的摇摄动作和曝光变化时，即使是这种方法也可能不起作用，这在随便获取的全景图中很常见。在这种情况下，一次或多次曝光可能会看到图像的不同部分。设计一种方法来融合所有这些不同的光源，同时避免急剧的过渡并处理场景运动，这是一项具有挑战性的任务，最近已通过首先找到共识镶嵌图，然后选择性地计算曝光不足和曝光过度区域的辐射来解决(Eden等(2006年)。

从长远来看，通过相机传感器技术的进步可以消除从多次曝光中计算高动态范围图像的需要(Yang等人，1999； Nayar和Mitsunaga，2000； Kang等人，2003； Tumblin等人，2005)。 但是，可能仍然需要混合此类图像并将其色调映射为令人愉悦的最终结果。

7扩展和未解决的问题

在本文中，我研究了图像对齐和拼接的基础知识，重点研究了记录部分重叠的图像并将其融合以创建无缝全景的技术。已经开发出许多其他技术来解决相关问题，例如通过拍摄多张位移的图片来提高图像的分辨率(超分辨率)，将视频拼接在一起以创建动态全景图以及在存在大量视差的情况下拼接视频和图像。

与图像拼接有关的最常见问题可能是以下内容。 “为什么您不可以只拍摄同一场景中具有亚像素位移的多张图像并生成具有更高有效分辨率的图像？”确实，这个问题已经研究了很长时间，通常被称为多图像超²³解决这一问题的论文实例包括(Keren等人，1988； Irani和Peleg，1991； Cheeseman等人，1993； Capel和Zisserman，1998； Capel和Zisserman，2000； Chaudhuri，2001)。 (参见(Baker and Kanade 2002)，其中包含大量其他参考文献和实验比较的最新论文。)总体思路是，同一场景的不同图像是从略有不同的位置(例如，像素无法准确采样空间中的相同光线)比单个图像包含更多的信息。但是，仅当成像器实际混叠了原始信号时(例如，硅传感器在有限区域内积分且光学器件未切断奈奎斯特频率以上的所有频率)，这才是正确的。运动估计也必须非常准确才能使它起作用，因此在实践中，很难实现大于2倍的分辨率提高(Baker和Kanade 2002)。

　　23也可以使用各种非线性或基于示例的插值技术来提高单个图像的分辨率(Freeman等，2002； Baker和Kanade，2002)。

另一个受欢迎的话题是视频拼接(Teodosio和Bender，1993； Massey和Bender，1996； Sawhney和Ayer，1996； Irani和Anandan，1998； Baudisch等人，2005； Steeled等人，2005)。尽管从许多方面来看，此问题都是多图像拼接的直接概括，但可能存在大量独立运动，相机缩放以及对动态事件进行可视化的需求，这带来了其他挑战。例如，经常可以使用中值滤波来移除移动的前景对象。或者，可以将前景对象提取到单独的图层中(Sawhney和Ayer，1996年)，然后再合成回缝合的全景图中，有时作为多个实例以产生“ Chronophotograph”的印象(Massey和Bender，1996年)，有时作为视频叠加层(Irani and Anandan 1998)。视频还可以用于创建动画全景视频纹理，其中通过独立移动的视频循环对全景场景的不同部分进行动画处理(Agarwala等人，2005； Rav-Acha等。

视频还可以提供有趣的内容源，用于创建从移动摄像机拍摄的全景图。尽管这使单视点(光学中心)的通常假设无效，但仍可以获得有趣的结果。例如，VideoBrush系统(Sawhney等人，1998)使用从图像中心获取的细条创建从水平移动相机获取的全景。使用自适应流形上的镶嵌概念可以将此思想推广到其他相机运动和合成表面(Peleg等人，2000年)。相关思想已被用于为多平面单元动画创建全景遮罩画(Wood等人，1997)，用于创建具有视差场景的缝合图像(Kumar等人，1995)，以及作为使用多个对象的更复杂场景的3D表示。投影中心图像(Rademacher和Bishop 1998)。

基于视频的全景图的另一个有趣的变化是同心镶嵌(Shum and He 1999)。在这里，而不是尝试生成单个全景图像，而是保留了完整的原始视频，并使用光线重新映射(光源渲染)将其重新合成了新颖的视图(来自不同的相机源)，从而使全景图具有3D感。深度。相同的数据集也可以用于使用多基线立体声显式地重建深度(Shum和Szeliski 1999，Shum等人1999，Peleg等人2001，Li等人2004b)。

开放式问题。到目前为止，虽然图像拼接已成为各种商业产品的相当成熟的领域，但仍然存在大量挑战和开放扩展。其中之一是提高全自动缝合算法的可靠性。正如第5.3节中讨论的以及图19和20所示，很难同时避免匹配虚假特征或重复模式，同时还要容忍较大的异常值，例如移动的人。语义场景理解方面的进步可以帮助解决其中一些问题，以及更好的机器学习技术来进行特征匹配和验证。

视差问题也没有得到充分解决。对于少量视差，第5.2节和第6.2节中描述的反虚幻技术通常可以通过局部变形和仔细的接缝选择来充分掩盖这些影响。对于高重叠全景图，可以使用同心镶嵌(同心镶嵌)(Shum和He，1999)，具有视差的全景(Li等人，2004b)和仔细的接缝选择(在潜在的用户指导下)(Agarwala等人，2004)。最具挑战性的情况是有限的具有大视差的重叠全景图，因为补偿视差所需的深度估计仅在重叠区域中可用(Kang等人，2004； Uyttendaele等人，2004)。

参考文献

Agarwala, A. et al.. (2004). Interactive digital photomontage. ACM Transactions on Graphics, 23(3), 292–300.
Agarwala, A. et al.. (2005). Panoramic video textures. ACM Transactions on Graphics, 24(3), 821–827.
Anandan, P. (1989). A computational framework and an algorithm for the measurement of visual motion. International Journal of Computer Vision, 2(3), 283–310.
Argyriou, V. and Vlachos, T. (2003). Estimation of sub-pixel motion using gradient crosscorrelation. Electronic Letters, 39(13), 980–982.
Ayache, N. (1989). Vision St´er´eoscopique et Perception Multisensorielle. InterEditions., Paris.
Bab-Hadiashar, A. and Suter, D. (1998). Robust total least squares based optic flow computation. In Asian Conference on Computer Vision (ACCV’98), pages 566–573, ACM, Hong Kong.
Badra, F., Qumsieh, A., and Dudek, G. (1998). Rotation and zooming in image mosaicing. In IEEE Workshop on Applications of Computer Vision (WACV’98), pages 50–55, IEEE Computer Society, Princeton.
Baker, S. and Kanade, T. (2002). Limits on super-resolution and how to break them. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(9), 1167–1183.
Baker, S. and Matthews, I. (2004). Lucas-Kanade 20 years on: A unifying framework: Part 1: The quantity approximated, the warp update rule, and the gradient descent approximation. International Journal of Computer Vision, 56(3), 221–255.
Baker, S. et al.. (2003a). Lucas-Kanade 20 Years On: A Unifying Framework: Part 2. Technical Report CMU-RI-TR-03-01, The Robotics Institute, Carnegie Mellon University.
Baker, S. et al.. (2003b). Lucas-Kanade 20 Years On: A Unifying Framework: Part 3. Technical Report CMU-RI-TR-03-35, The Robotics Institute, Carnegie Mellon University.
Baker, S. et al.. (2004). Lucas-Kanade 20 Years On: A Unifying Framework: Part 4. Technical Report CMU-RI-TR-04-14, The Robotics Institute, Carnegie Mellon University.
Barreto, J. and Daniilidis, K. (2005). Fundamental matrix for cameras with radial distortion. In Tenth International Conference on Computer Vision (ICCV 2005), pages 625–632, Beijing,China.

Bartoli, A., Coquerelle, M., and Sturm, P. (2004). A framework for pencil-of-points structurefrom-motion. In Eighth European Conference on Computer Vision (ECCV 2004), pages 28–40, Springer-Verlag, Prague.
Baudisch, P. et al.. (2005). Panoramic viewfinder: providing a real-time preview to help users avoid flaws in panoramic pictures. In OZCHI 2005, Canberra, Australia.
Baumberg, A. (2000). Reliable feature matching across widely separated views. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2000), pages 774–781, Hilton Head Island.
Bay, H., Tuytelaars, T., and Gool, L. V. (2006). Surf: Speeded up robust features. In Leonardis, A., Bischof, H., and Pinz, A., editors, Computer Vision – ECCV 2006, pages 404–417, Springer.
Beis, J. S. and Lowe, D. G. (1997). Shape indexing using approximate nearest-neighbour search in high-dimensional spaces. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’97), pages 1000–1006, San Juan, Puerto Rico.
Benosman, R. and Kang, S. B., editors. (2001). Panoramic Vision: Sensors, Theory, and Applications, Springer, New York.
Bergen, J. R., Anandan, P., Hanna, K. J., and Hingorani, R. (1992a). Hierarchical model-based motion estimation. In Second European Conference on Computer Vision (ECCV’92), pages 237–252, Springer-Verlag, Santa Margherita Liguere, Italy.
Bergen, J. R., Burt, P. J., Hingorani, R., and Peleg, S. (1992b). A three-frame algorithm for estimating two-component image motion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14(9), 886–896.
Black, M. J. and Anandan, P. (1996). The robust estimation of multiple motions: Parametric and piecewise-smooth flow fields. Computer Vision and Image Understanding, 63(1), 75–104.
Black,M. J. and Jepson, A. D. (1998). EigenTracking: robustmatching and tracking of articulated objects using a view-based representation. International Journal of Computer Vision, 26(1), 63–84.
Black, M. J. and Rangarajan, A. (1996). On the unification of line processes, outlier rejection, and robust statistics with applications in early vision. International Journal of Computer Vision, 19(1), 57–91.
Blinn, J. F. (1994). Jim Blinn’s corner: Compositing, part 1: Theory. IEEE Computer Graphics and Applications, 14(5), 83–87.

Borgefors, G. (1986). Distance transformations in digital images. Computer Vision, Graphics and Image Processing, 34(3), 227–248.
Boykov, Y., Veksler, O., and Zabih, R. (2001). Fast approximate energy minimization via graph cuts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(11), 1222–1239.
Brown, D. C. (1971). Close-range camera calibration. Photogrammetric Engineering, 37(8), 855–866.
Brown, L. G. (1992). A survey of image registration techniques. Computing Surveys, 24(4), 325–376.
Brown, M. and Lowe, D. (2003). Recognizing panoramas. In Ninth International Conference on Computer Vision (ICCV’03), pages 1218–1225, Nice, France.
Brown, M., Szeliski, R., and Winder, S. (2004). Multi-Image Matching Using Multi-Scale Oriented Patches. Technical Report MSR-TR-2004-133, Microsoft Research.
Brown, M., Szeliski, R., andWinder, S. (2005). Multi-image matching using multi-scale oriented patches. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 510–517, San Diego, CA.
Bugayevskiy, L. M. and Snyder, J. P. (1995). Map Projections: A Reference Manual. CRC Press.
Burt, P. J. and Adelson, E. H. (1983). Amultiresolution splinewith applications to imagemosaics. ACM Transactions on Graphics, 2(4), 217–236.
Capel, D. and Zisserman, A. (1998). Automated mosaicing with super-resolution zoom. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’98), pages 885–891, Santa Barbara.
Capel, D. and Zisserman, A. (2000). Super-resolution enhancement of text image sequences. In Fifteenth International Conference on Pattern Recognition (ICPR’2000), pages 600–605, IEEE Computer Society Press, Barcelona, Spain.
Carneiro, G. and Jepson, A. (2005). The distinctiveness, detectability, and robustness of local image features. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 296–301, San Diego, CA.
Cham, T. J. and Cipolla, R. (1998). A statistical framework for long-range feature matching in uncalibrated image mosaicing. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’98), pages 442–447, Santa Barbara.

Champleboux, G. et al.. (1992). Accurate calibration of cameras and range imaging sensors, the NPBS method. In IEEE International Conference on Robotics and Automation, pages 1552–1558, IEEE Computer Society Press, Nice, France.
Chaudhuri, S. (2001). Super-Resolution Imaging. Springer.
Cheeseman, P., Kanefsky, B., Hanson, R., and Stutz, J. (1993). Super-Resolved Surface Reconstruction From Multiple Images. Technical Report FIA-93-02, NASA Ames Research Center, Artificial Intelligence Branch.
Chen, C.-Y. and Klette, R. (1999). Image stitching - comparisons and new techniques. In Computer Analysis of Images and Patterns (CAIP’99), pages 615–622, Springer-Verlag, Ljubljana.
Chen, S. E. (1995). QuickTime VR – an image-based approach to virtual environment navigation. Computer Graphics (SIGGRAPH’95), , 29–38.
Chum, O. and Matas, J. (2005). Matching with prosac — progressive sample consensus. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 220–226, San Diego, CA.
Claus, D. and Fitzgibbon, A. (2005). A rational function lens distortion model for general cameras. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 213–219, San Diego, CA.
Coorg, S. and Teller, S. (2000). Spherical mosaics with quaternions and dense correlation. International Journal of Computer Vision, 37(3), 259–273.
Corso, J. and Hager, G. (2005). Coherent regions for concise and stable image description. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 184–190, San Diego, CA.
Cox, I. J., Roy, S., and Hingorani, S. L. (1995). Dynamic histogram warping of image pairs for constant image brightness. In IEEE International Conference on Image Processing (ICIP’95), pages 366–369, IEEE Computer Society.
Danielsson, P. E. (1980). Euclidean distance mapping. Computer Graphics and Image Processing, 14(3), 227–248.
Davis, J. (1998). Mosaics of scenes with moving objects. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’98), pages 354–360, Santa Barbara.

De Castro, E. and Morandi, C. (1987). Registration of translated and rotated iimages using finite fourier transforms. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-9(5), 700–703.
Debevec, P. E. and Malik, J. (1997). Recovering high dynamic range radiance maps from photographs. Proceedings of SIGGRAPH 97, , 369–378. ISBN 0-89791-896-7. Held in Los Angeles, California.
Dellaert, F. and Collins, R. (1999). Fast image-based tracking by selective pixel integration. In ICCV Workshop on Frame-Rate Vision, pages 1–22.
Durand, F. and Dorsey, J. (2002). Fast bilateral filtering for the display of high-dynamic-range images. ACM Transactions on Graphics (TOG), 21(3), 257–266.
Eden, A., Uyttendaele,M., and Szeliski, R. (2006). Seamless image stitching of scenes with large motions and exposure differences. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2006), pages 2498–2505, New York, NY.
Efros, A. A. and Freeman, W. T. (2001). Image quilting for texture synthesis and transfer. In Fiume, E., editor, SIGGRAPH 2001, Computer Graphics Proceedings, pages 341–346, ACM Press / ACM SIGGRAPH.
El-Melegy, M. and Farag, A. (2003). Nonmetric lens distortion calibration: Closed-form solutions, robust estimation and model selection. In Ninth International Conference on Computer Vision (ICCV 2003), pages 554–559, Nice, France.
Elder, J. H. and Golderg, R. M. (2001). Image editing in the contour domain. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(3), 291–296.
Fattal, R., Lischinski, D., and Werman, M. (2002). Gradient domain high dynamic range compression. ACM Transactions on Graphics (TOG), 21(3), 249–256.
Fischler, M. A. and Bolles, R. C. (1981). Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24(6), 381–395.
Fleet, D. and Jepson, A. (1990). Computation of component image velocity from local phase information. International Journal of Computer Vision, 5(1), 77–104.
F¨orstner, W. (1986). A feature-based correspondence algorithm for image matching. Intl. Arch. Photogrammetry & Remote Sensing, 26(3), 150–166.

F¨orstner,W. (1994). A framework for low level feature extraction. In Third European Conference on Computer Vision (ECCV’94), pages 383–394, Springer-Verlag, Stockholm, Sweden.
Freeman, W. T. and Adelson, E. H. (1991). The design and use of steerable filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(9), 891–906.
Freeman, W. T., Jones, T. R., and Pasztor, E. C. (2002). Example-based super-resolution. IEEE Computer Graphics and Applications, 22(2), 56–65.
Fuh, C.-S. and Maragos, P. (1991). Motion displacement estimation using an affine model for image matching. Optical Engineering, 30(7), 881–887.
Geman, S. and Geman, D. (1984). Stochastic relaxation, Gibbs distribution, and the Bayesian
restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-6(6), 721–741.
Gennert, M. A. (1988). Brightness-based stereo matching. In Second International Conference on Computer Vision (ICCV’88), pages 139–143, IEEE Computer Society Press, Tampa.
Golub, G. and Van Loan, C. F. (1996). Matrix Computation, third edition. The John Hopkins University Press, Baltimore and London.
Goshtasby, A. (1989). Correction of image deformation from lens distortion using bezier patches. Computer Vision, Graphics, and Image Processing, 47(4), 385–394.
Goshtasby, A. (2005). 2-D and 3-D Image Registration. Wiley, New York.
Govindu, V. M. (2006). Revisiting the brightness constraint: Probabilistic formulation and algorithms. In Leonardis, A., Bischof, H., and Pinz, A., editors, Computer Vision – ECCV 2006, pages 177–188, Springer.
Greene, N. (1986). Environment mapping and other applications of world projections. IEEE Computer Graphics and Applications, 6(11), 21–29.
Greene, N. and Heckbert, P. (1986). Creating raster Omnimax images from multiple perspective views using the elliptical weighted average filter. IEEE Computer Graphics and Applications, 6(6), 21–27.
Gremban, K. D., Thorpe, C. E., and Kanade, T. (1988). Geometric camera calibration using systems of linear equations. In IEEE International Conference on Robotics and Automation, pages 562–567, IEEE Computer Society Press, Philadelphia.

Grossberg, M. D. and Nayar, S. K. (2001). A general imaging model and a method for finding its parameters. In Eighth International Conference on Computer Vision (ICCV 2001), pages 108–115, Vancouver, Canada.
Hager, G. D. and Belhumeur, P. N. (1998). Efficient region tracking with parametric models of geometry and illumination. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(10), 1025–1039.
Hampel, F. R. et al.. (1986). Robust Statistics : The Approach Based on Influence Functions. Wiley, New York.
Hannah, M. J. (1974). Computer Matching of Areas in Stereo Images. Ph.D. thesis, Stanford University.
Hannah, M. J. (1988). Test results from SRI’s stereo system. In Image Understanding Workshop, pages 740–744, Morgan Kaufmann Publishers, Cambridge, Massachusetts.
Hansen, M., Anandan, P., Dana, K., van der Wal, G., and Burt, P. (1994). Real-time scene stabilization and mosaic construction. In IEEE Workshop on Applications of Computer Vision (WACV’94), pages 54–62, IEEE Computer Society, Sarasota.
Harris, C. and Stephens, M. J. (1988). A combined corner and edge detector. In Alvey Vision Conference, pages 147–152.
Hartley, R. and Kang, S. B. (2005). Parameter-free radial distortion correction with centre of distortion estimation. In Tenth International Conference on Computer Vision (ICCV 2005), pages 1834–1841, Beijing, China.
Hartley, R. I. (1994). Self-calibration from multiple views of a rotating camera. In Third European
Conference on Computer Vision (ECCV’94), pages 471–478, Springer-Verlag, Stockholm, Sweden.
Hartley, R. I. and Zisserman, A. (2000). Multiple View Geometry. Cambridge University Press, Cambridge, UK.
Hartley, R. I. and Zisserman, A. (2004). Multiple View Geometry. Cambridge University Press, Cambridge, UK.
Herley, C. (2005). Automatic occlusion removal from minimum number of images. In International Conference on Image Processing (ICIP 2005), pages 1046–1049–16, Genova.

Horn, B. K. P. (1974). Determining lightness from an image. Computer Graphics and Image Processing, 3(1), 277–299.
Horn, B. K. P. (1986). Robot Vision. MIT Press, Cambridge, Massachusetts.
Horn, B. K. P. and Brooks, M. J. (1989). Shape from Shading. MIT Press, Cambridge, Massachusetts.
Horn, B. K. P. and Schunck, B. G. (1981). Determining optical flow. Artificial Intelligence, 17, 185–203.
Huber, P. J. (1981). Robust Statistics. John Wiley & Sons, New York.
Huffel, S. v. and Vandewalle, J. (1991). The Total Least Squares Problem: Computational Aspects and Analysis. Society for Industrial and Applied Mathematics, Philadephia.
Irani, M. and Anandan, P. (1998). Video indexing based on mosaic representations. Proceedings of the IEEE, 86(5), 905–921.
Irani, M. and Anandan, P. (1999). About direct methods. In International Workshop on Vision Algorithms, pages 267–277, Springer, Kerkyra, Greece.
Irani, M. and Peleg, S. (1991). Improving resolution by image registration. Graphical Models and Image Processing, 53(3), 231–239.
Irani, M., Hsu, S., and Anandan, P. (1995). Video compression using mosaic representations. Signal Processing: Image Communication, 7, 529–552.
Jia, J. and Tang, C.-K. (2003). Image registration with global and local luminance alignment. In Ninth International Conference on Computer Vision (ICCV 2003), pages 156–163, Nice, France.
Jurie, F. and Dhome, M. (2002). Hyperplane approximation for template matching. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(7), 996–1000.
Kadir, T. and Brady, M. (2001). Saliency, scale and image description. International Journal of Computer Vision, 45(2), 83–105.
Kadir, T., Zisserman, A., and Brady, M. (2004). An affine invariant salient region detector. In Eighth European Conference on Computer Vision (ECCV 2004), pages 228–241, Springer-Verlag, Prague.
Kang, S. B. (2001). Radial distortion snakes. IEICE Trans. Inf. & Syst., E84-D(12), 1603–1611.

Kang, S. B. et al.. (2003). High dynamic range video. ACM Transactions on Graphics, 22(3),319–325.
Kang, S. B. and Weiss, R. (1997). Characterization of errors in compositing panoramic images. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’97), pages 103–109, San Juan, Puerto Rico.
Kang, S. B., Szeliski, R., and Uyttendaele,M. (2004). Seamless Stitching usingMulti-Perspective Plane Sweep. Technical Report MSR-TR-2004-48, Microsoft Research.
Ke, Y. and Sukthankar, R. (2004). PCA-SIFT: a more distinctive representation for local image descriptors. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2004), pages 506–513, Washington, DC.
Kenney, C., Zuliani, M., and Manjunath, B. (2005). An axiomatic approach to corner detection. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 191–197, San Diego, CA.
Keren, D., Peleg, S., and Brada, R. (1988). Image sequence enhancement using sub-pixel displacements. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’88), pages 742–746, IEEE Computer Society Press, Ann Arbor, Michigan.
Kim, J., Kolmogorov,V., and Zabih, R. (2003). Visual correspondence using energy minimization and mutual information. In Ninth International Conference on Computer Vision (ICCV 2003), pages 1033–1040, Nice, France.
Kuglin, C. D. and Hines, D. C. (1975). The phase correlation image alignment method. In IEEE 1975 Conference on Cybernetics and Society, pages 163–165, New York.
Kumar, R., Anandan, P., and Hanna, K. (1994). Direct recovery of shape from multiple views: A parallax based approach. In Twelfth International Conference on Pattern Recognition (ICPR’94), pages 685–688, IEEE Computer Society Press, Jerusalem, Israel.
Kumar, R., Anandan, P., Irani, M., Bergen, J., and Hanna, K. (1995). Representation of scenes from collections of images. In IEEEWorkshop on Representations of Visual Scenes, pages 10–17, Cambridge, Massachusetts.
Kwatra, V. et al.. (2003). Graphcut textures: Image and video synthesis using graph cuts. ACM Transactions on Graphics, 22(3), 277–286.
Le Gall, D. (1991). MPEG: A video compression standard for multimedia applications. Communications of the ACM, 34(4), 44–58.

Lee, M.-C. et al.. (1997). A layered video object coding system using sprite and affine motion model. IEEE Transactions on Circuits and Systems for Video Technology, 7(1), 130–145.
Levin, A., Zomet, A., and Weiss, Y. (2004a). Separating reflections from a single image using local features. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2004), pages 306–313, Washington, DC.
Levin, A., Zomet, A., Peleg, S., and Weiss, Y. (2004b). Seamless image stitching in the gradient domain. In Eighth European Conference on Computer Vision (ECCV 2004), pages 377–389, Springer-Verlag, Prague.
Li, Y. et al.. (2004a). Lazy snapping. ACM Transactions on Graphics, 23(3), 303–308.
Li, Y. et al.. (2004b). Stereo reconstruction from multiperspective panoramas. IEEE Transactions on Pattern Analysis and Machine Intelligence, 26(1), 44–62.
Lindeberg, T. (1990). Scale-space for discrete signals. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(3), 234–254.
Lischinski, D., Farbman, Z., Uytendaelle, M., and Szeliski, R. (2006). Interactive local adjustment of tonal values. ACM Transactions on Graphics, 25(3), 646–653.
Loop, C. and Zhang, Z. (1999). Computing rectifying homographies for stereo vision. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’99), pages 125–131, Fort Collins.
Lowe, D. G. (2004). Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 60(2), 91–110.
Lucas, B. D. and Kanade, T. (1981). An iterative image registration technique with an application in stereo vision. In Seventh International Joint Conference on Artificial Intelligence (IJCAI-81), pages 674–679, Vancouver.
Mann, S. and Picard, R. W. (1994). Virtual bellows: Constructing high-quality images from video. In First IEEE International Conference on Image Processing (ICIP-94), pages 363–367, Austin.
Mann, S. and Picard, R.W. (1995). On being ‘undigital’ with digital cameras: Extending dynamic range by combining differently exposed pictures. In IS&T’s 48th Annual Conference, pages 422–428, Society for Imaging Science and Technology, Washington, D. C.

Massey, M. and Bender, W. (1996). Salient stills: Process and practice. IBM Systems Journal, 35(3&4), 557–573.
Matas, J. et al.. (2004). Robust wide baseline stereo from maximally stable extremal regions. Image and Vision Computing, 22(10), 761–767.
Matthies, L. H., Szeliski, R., and Kanade, T. (1989). Kalman filter-based algorithms for estimating depth from image sequences. International Journal of Computer Vision, 3, 209–236.
McLauchlan, P. F. and Jaenicke, A. (2002). Image mosaicing using sequential bundle adjustment. Image and Vision Computing, 20(9-10), 751–759.
McMillan, L. and Bishop, G. (1995). Plenoptic modeling: An image-based rendering system. Computer Graphics (SIGGRAPH’95), , 39–46.
Meehan, J. (1990). Panoramic Photography. Watson-Guptill.
Mikolajczyk, K. et al.. (2005). A comparison of affine region detectors. International Journal of Computer Vision, 65(1-2), 43–72.
Mikolajczyk, K. and Schmid, C. (2004). Scale & affine invariant interest point detectors. International Journal of Computer Vision, 60(1), 63–86.
Mikolajczyk, K. and Schmid, C. (2005). A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(10), 1615–1630.
Milgram, D. L. (1975). Computer methods for creating photomosaics. IEEE Transactions on Computers, C-24(11), 1113–1119.
Milgram, D. L. (1977). Adaptive techniques for photomosaicking. IEEE Transactions on Computers, C-26(11), 1175–1180.
Mitsunaga, T. and Nayar, S. K. (1999). Radiometric self calibration. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’99), pages 374–380, Fort Collins.
Moravec, H. (1983). The stanford cart and the cmu rover. Proceedings of the IEEE, 71(7), 872–884.
M¨uhlich, M. and Mester, R. (1998). The role of total least squares in motion analysis. In Fifth European Conference on Computer Vision (ECCV’98), pages 305–321, Springer-Verlag, Freiburg, Germany.

Nayar, S. K. and Mitsunaga, T. (2000). High dynamic range imaging: Spatially varying pixel exposures. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2000), pages 472–479, Hilton Head Island.
Nene, S. and Nayar, S. K. (1997). A simple algorithm for nearest neighbor search in high dimensions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 19(9), 989–1003.
Nielson, G. M. (1993). Scattered data modeling. IEEE Computer Graphics and Applications, 13(1), 60–70.
Nister, D. and Stewenius, H. (2006). Scalable recognition with a vocabulary tree. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2006), pages 2161–2168, New York City, NY.
Okutomi, M. and Kanade, T. (1993). A multiple baseline stereo. IEEE Transactions on Pattern Analysis and Machine Intelligence, 15(4), 353–363.
OpenGL-ARB. (1997). OpenGL Reference Manual: The Official Reference Document to OpenGL, Version 1.1. Addison-Wesley, Reading, MA, 2nd edition.
Oppenheim, A. V., Schafer, R. W., and Buck, J. R. (1999). Discrete-Time Signal Processing. Pearson Education, 2nd edition.
Peleg, R., Ben-Ezra, M., and Pritch, Y. (2001). Omnistereo: Panoramic stereo imaging. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(3), 279–290.
Peleg, S. (1981). Elimination of seams from photomosaics. Computer Vision, Graphics, and Image Processing, 16, 1206–1210.
Peleg, S. et al.. (2000). Mosaicing on adaptive manifolds. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(10), 1144–1154.
Peleg, S. and Rav-Acha, A. (2006). Lucas-Kanade without iterative warping. In International Conference on Image Processing (ICIP-2006), pages 1097–1100, Atlanta.
P´erez, P., Gangnet, M., and Blake, A. (2003). Poisson image editing. ACM Transactions on Graphics, 22(3), 313–318.
Platel, B., Balmachnova, E., Florack, L., and ter Haar Romeny, B. (2006). Top-points as interest points for image matching. In Leonardis, A., Bischof, H., and Pinz, A., editors, Computer Vision– ECCV 2006, pages 418–429, Springer.

Porter, T. and Duff, T. (1984). Compositing digital images. Computer Graphics (SIGGRAPH’84),18(3), 253–259.
Quam, L. H. (1984). Hierarchical warp stereo. In Image Understanding Workshop, pages 149–155, Science Applications International Corporation, New Orleans.
Rademacher, P. and Bishop, G. (1998). Multiple-center-of-projection images. In Computer Graphics Proceedings, Annual Conference Series, pages 199–206, ACMSIGGRAPH, Proc. SIGGRAPH’ 98 (Orlando).
Rav-Acha, A., Pritch, Y., Lischinski, D., and Peleg, S. (2005). Dynamosaics: Video mosaics with non-chronological time. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 58–65, San Diego, CA.
Rehg, J. and Witkin, A. (1991). Visual tracking with deformation models. In IEEE International Conference on Robotics and Automation, pages 844–850, IEEE Computer Society Press, Sacramento.
Reinhard, E. et al.. (2002). Photographic tone reproduction for digital images. ACM Transactions on Graphics (TOG), 21(3), 267–276.
Reinhard, E., Ward, G., Pattanaik, S., and Debevec, P. (2005). High Dynamic Range Imaging: Acquisition, Display, and Image-Based Lighting. Morgan Kaufmann.
Rosten, E. and Drummond, T. (2006). Machine learning for high-speed corner detection. In Leonardis, A., Bischof, H., and Pinz, A., editors, Computer Vision – ECCV 2006, pages 430–443, Springer.
Rother, C., Kolmogorov, V., and Blake, A. (2004). “GrabCut” - interactive foreground extraction using iterated graph cuts. ACM Transactions on Graphics, 23(3), 309–314.
Rousseeuw, P. J. (1984). Least median of squares regresssion. Journal of the American Statistical Association, 79, 871–880.
Rousseeuw, P. J. and Leroy, A. M. (1987). Robust Regression and Outlier Detection. Wiley, New York.
Samet, H. (1989). The Design and Analysis of Spatial Data Structures. Addison-Wesley, Reading, Massachusetts.
Sawhney, H. S. (1994). 3D geometry from planar parallax. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’94), pages 929–934, IEEE Computer Society, Seattle.

Sawhney, H. S. and Ayer, S. (1996). Compact representation of videos through dominant multiple motion estimation. IEEE Transactions on Pattern Analysis andMachine Intelligence, 18(8), 814–830.
Sawhney, H. S. and Kumar, R. (1999). True multi-image alignment and its application to mosaicing and lens distortion correction. IEEE Transactions on Pattern Analysis and Machine Intelligence, 21(3), 235–243.
Sawhney, H. S. et al.. (1998). Videobrush: Experiences with consumer video mosaicing. In IEEE Workshop on Applications of Computer Vision (WACV’98), pages 56–62, IEEE Computer Society, Princeton.
Schaffalitzky, F. and Zisserman, A. (2002). Multi-view matching for unordered image sets, or“How do I organize my holiday snaps?”. In Seventh European Conference on Computer Vision (ECCV 2002), pages 414–431, Springer-Verlag, Copenhagen.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. International Journal of Computer Vision, 47(1), 7–42.
Schmid, C., Mohr, R., and Bauckhage, C. (2000). Evaluation of interest point detectors. International Journal of Computer Vision, 37(2), 151–172.
Shakhnarovich, G., Viola, P., and Darrell, T. (2003). Fast pose estimation with parameter sensitive hashing. In Ninth International Conference on Computer Vision (ICCV 2003), pages 750–757, Nice, France.
Shi, J. and Tomasi, C. (1994). Good features to track. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’94), pages 593–600, IEEE Computer Society, Seattle.
Shoemake, K. (1985). Animating rotation with quaternion curves. Computer Graphics (SIGGRAPH’85), 19(3), 245–254.
Shum, H.-Y. and He, L.-W. (1999). Rendering with concentric mosaics. In SIGGRAPH’99, pages 299–306, ACM SIGGRAPH, Los Angeles.
Shum, H.-Y. et al.. (1999). Omnivergenet stereo. In Seventh International Conference on Computer Vision (ICCV’99), pages 22–29, Greece.
Shum, H.-Y. and Szeliski, R. (1997). Panoramic Image Mosaicing. Technical Report MSR-TR-97-23, Microsoft Research.

Shum, H.-Y. and Szeliski, R. (1999). Stereo reconstruction from multiperspective panoramas. In Seventh International Conference on Computer Vision (ICCV’99), pages 14–21, Kerkyra, Greece.
Shum, H.-Y. and Szeliski, R. (2000). Construction of panoramic mosaics with global and local alignment. International Journal of Computer Vision, 36(2), 101–130. Erratum published July 2002, 48(2):151-152.
Simoncelli, E. P., Adelson, E. H., and Heeger, D. J. (1991). Probability distributions of optic flow. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’91), pages 310–315, IEEE Computer Society Press, Maui, Hawaii.
Slama, C. C., editor. (1980). Manual of Photogrammetry. American Society of Photogrammetry, Falls Church, Virginia, fourth edition.
Soille, P. (2006). Morphological image compositing. IEEE Transactions on Pattern Analysis and Machine Intelligence, 28(5), 673–683.
Steedly, D. et al.. (2005). Efficiently registering video into panoramic mosaics. In Tenth International Conference on Computer Vision (ICCV 2005), pages 1300–1307, Beijing, China.
Steele, R. and Jaynes, C. (2005). Feature uncertainty arising from covariant image noise. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 1063–1070, San Diego, CA.
Steele, R. M. and Jaynes, C. (2006). Overconstrained linear estimation of radial distortion and multi-view geometry. In Leonardis, A., Bischof, H., and Pinz, A., editors, Computer Vision – ECCV 2006, pages 253–264, Springer.
Stein, G. (1995). Accurate internal camera calibration using rotation, with analysis of sources of error. In Fifth International Conference on Computer Vision (ICCV’95), pages 230–236, Cambridge, Massachusetts.
Stein, G. (1997). Lens distortion calibration using point correspondences. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’97), pages 602–608, San Juan, Puerto Rico.
Stewart, C. V. (1999). Robust parameter estimation in computer vision. SIAM Reviews, 41(3), 513–537.
Sturm, P. (2005). Multi-view geometry for general camera models. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 206–212, San Diego, CA.

Sun, J., Zheng, N., and Shum, H. (2003). Stereo matching using belief propagation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25(7), 787–800.
Szeliski, R. (1989). Bayesian Modeling of Uncertainty in Low-Level Vision. Kluwer Academic Publishers, Boston.
Szeliski, R. (1990). Fast surface interpolation using hierarchical basis functions. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(6), 513–528.
Szeliski, R. (1994). Image mosaicing for tele-reality applications. In IEEE Workshop on Applications of Computer Vision (WACV’94), pages 44–53, IEEE Computer Society, Sarasota.
Szeliski, R. (1996). Video mosaics for virtual environments. IEEE Computer Graphics and Applications, 16(2), 22–30.
Szeliski, R. (2006). Locally adapted hierarchical basis preconditioning. ACM Transactions on Graphics, 25(3), 1135–1143.
Szeliski, R. and Coughlan, J. (1994). Hierarchical spline-based image registration. In IEEE Computer
Society Conference on Computer Vision and Pattern Recognition (CVPR’94), pages 194–201, IEEE Computer Society, Seattle.
Szeliski, R. and Kang, S. B. (1994). Recovering 3D shape and motion from image streams
using nonlinear least squares. Journal of Visual Communication and Image Representation, 5(1), 10–28.
Szeliski, R. and Kang, S. B. (1995). Direct methods for visual scene reconstruction. In IEEE Workshop on Representations of Visual Scenes, pages 26–33, Cambridge, Massachusetts.
Szeliski, R. and Shum, H.-Y. (1997). Creating full view panoramic image mosaics and texturemapped models. Computer Graphics (SIGGRAPH’97 Proceedings), , 251–258.
Tappen, M. F. and Freeman, W. T. (2003). Comparison of graph cuts with belief propagation for stereo, using identical MRF parameters. In Ninth International Conference on Computer Vision (ICCV 2003), pages 900–907, Nice, France. Tardif, J.-P. et al.. (2006a). Self-calibration of a general radially symmetric distortion model.
In Seventh European Conference on Computer Vision (ECCV 2002), pages 186–199, Springer- Verlag, Graz.
Tardif, J.-P., Sturm, P., and Roy, S. (2006b). Self-calibration of a general radially symmetric distortion model. In Leonardis, A., Bischof, H., and Pinz, A., editors, Computer Vision – ECCV 2006, pages 186–199, Springer.

Teodosio, L. and Bender, W. (1993). Salient video stills: Content and context preserved. In ACM Multimedia 93, pages 39–46, Anaheim, California.
Thirthala, S. and Pollefeys, M. (2005). The radial trifocal tensor: A tool for calibrating the radial distortion of wide-angle cameras. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 321–328, San Diego, CA.
Tian, Q. and Huhns, M. N. (1986). Algorithms for subpixel registration. Computer Vision, Graphics, and Image Processing, 35, 220–233.
Triggs, B. (2004). Detecting keypoints with stable position, orientation, and scale under illumination changes. In Eighth European Conference on Computer Vision (ECCV 2004), pages 100–113, Springer-Verlag, Prague.
Triggs, B. et al.. (1999). Bundle adjustment — a modern synthesis. In International Workshop on Vision Algorithms, pages 298–372, Springer, Kerkyra, Greece.
Tumblin, J., Agrawal, A., and Raskar, R. (2005). Why i want a gradient camera. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2005), pages 103–110, San Diego, CA.
Tuytelaars, T. and Van Gool, L. (2004). Matching widely separated views based on affine invariant regions. International Journal of Computer Vision, 59(1), 61–85.
Uyttendaele, M. et al.. (2004). Image-based interactive exploration of real-world environments. IEEE Computer Graphics and Applications, 24(3).
Uyttendaele, M., Eden, A., and Szeliski, R. (2001). Eliminating ghosting and exposure artifacts in image mosaics. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2001), pages 509–516, Kauai, Hawaii.
van de Weijer, J. and Schmid, C. (2006). Coloring local feature extraction. In Leonardis, A., Bischof, H., and Pinz, A., editors, Computer Vision – ECCV 2006, pages 334–348, Springer.
Viola, P. andWells III,W. (1995). Alignment by maximization of mutual information. In Fifth International Conference on Computer Vision (ICCV’95), pages 16–23, Cambridge,Massachusetts.
Wang, L., Kang, S. B., Szeliski, R., and Shum, H.-Y. (2001). Optimal texture map reconstruction from multiple views. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2001), pages 347–354, Kauai, Hawaii.
Watt, A. (1995). 3D Computer Graphics. Addison-Wesley, third edition.

Weber, J. and Malik, J. (1995). Robust computation of optical flow in a multi-scale differential framework. International Journal of Computer Vision, 14(1), 67–81.
Weiss, Y. (2001). Deriving intrinsic images from image sequences. In Eighth International Conference on Computer Vision (ICCV 2001), pages 7–14, Vancouver, Canada.
Williams, L. (1983). Pyramidal parametrics. Computer Graphics, 17(3), 1–11.
Wood, D. N. et al.. (1997). Multiperspective panoramas for cel animation. In Computer
Graphics Proceedings, Annual Conference Series, pages 243–250, ACMSIGGRAPH, Proc. SIGGRAPH’97 (Los Angeles).
Woodham, R. J. (1981). Analysing images of curved surfaces. Artificial Intelligence, 17, 117–140.
Xiong, Y. and Turkowski, K. (1997). Creating image-based VR using a self-calibrating fisheye lens. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’97), pages 237–243, San Juan, Puerto Rico.
Xiong, Y. and Turkowski, K. (1998). Registration, calibration and blending in creating high quality panoramas. In IEEE Workshop on Applications of Computer Vision (WACV’98), pages 69–74, IEEE Computer Society, Princeton.
Yang, D. et al.. (1999). A 640x512 CMOS image sensor with ultra-wide dynamic range floatingpoint pixel level ADC. IEEE Journal of Solid State Circuits, 34(12), 1821–1834.
Zabih, R. and Woodfill, J. (1994). Non-parametric local transforms for computing visual correspondence. In Third European Conference on Computer Vision (ECCV’94), pages 151–158, Springer-Verlag, Stockholm, Sweden.
Zitov’aa, B. and Flusser, J. (2003). Image registration methods: A survey. Image and Vision Computing, 21, 997–1000.
Zoghlami, I., Faugeras, O., and Deriche, R. (1997). Using geometric corners to build a 2D mosaic from a set of images. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’97), pages 420–425, San Juan, Puerto Rico.