参考:http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
2016-08-22
前言:自己看《算法导论》中关于KMP算法的讲解,文字描述+插图+伪代码,但最终还是云里雾里。之后借助于上面提到的博客才有所体会。感谢博主。
对于其最核心的部分---当模板字符串中前面q个字符和源字符串中的某个子串匹配时,如果继续往下匹配,发现两个字符并不相同,那该如何移动模板字符串进行比较呢?
1. 最简单的方法当然是,将模板字符串向后移动一位,继续从头开始比较每一个字符。很明显,这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
2. 就是利用KMP算法,设法利用前面已经比较过的q位字符串信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
那么KMP算法的移动方法是什么呢?
答案是:借助一个next数组(也称为部分匹配表)来计算下次字符串移动的位数应该是多少。
如下图所示:
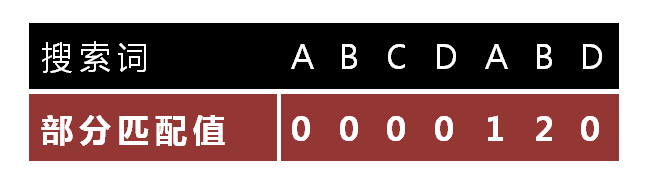
下面介绍部分匹配表是如何产生的:
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,(这只是相对于模板字符串而言,与源字符串无关)
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
例如:
- "A"的前缀和后缀都为空集,共有元素的长度为0; q=1
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0; q=2
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0; q=3
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0; q=4
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1; q=5
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2; q=6
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。 q=7
最后,模板字符串移动的位数 = q - 部分匹配值。(其中q表示已经匹配的字符的个数。)
" 部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长 度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度(q) - 部分匹配值),就可以来到第二个"AB"的位置。

所以,通过避免一些不必要的比较,这样就可以提高算法效率,时间复杂度为O(m+n),而一般方法复杂度为O(m×n)。
算法理解,到此就清楚了,实现代码如下:
简单匹配算法的时间复杂度为O(m*n),KMP匹配算法,可以证明它的时间复杂度为O(m+n).。