牛顿法步骤:
1. 以y = (x - 2) * (x - 2) 函数为例,先任意选取一点A,在曲线上做A点的切线,交X轴与B点,在B做X轴的垂线,交曲线于C点。
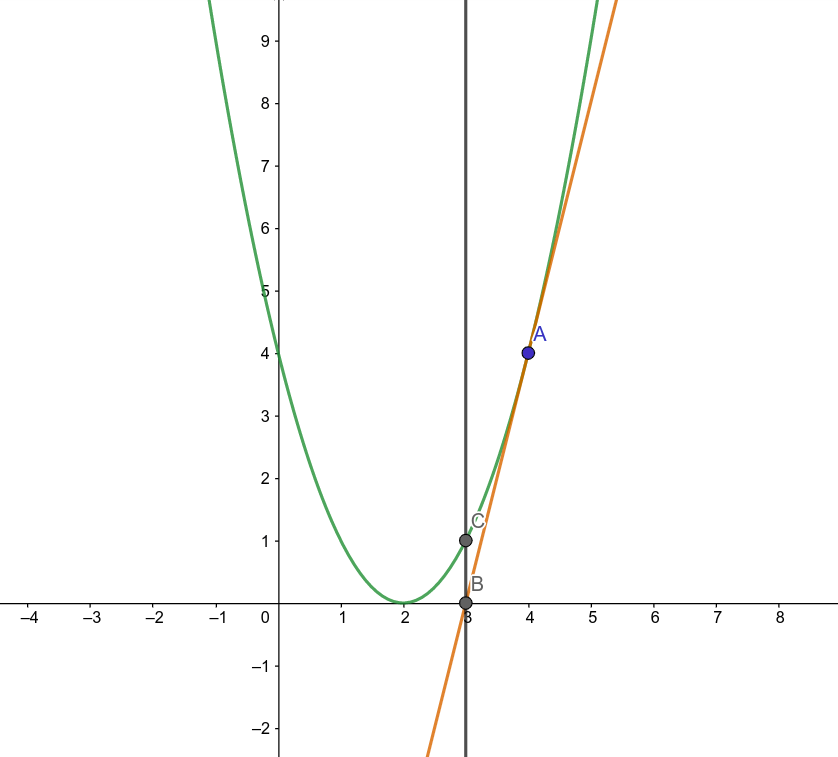
2. 在曲线上做C点的切线,交X轴与D点,在D点做X轴的垂线,交曲线于E点。我们可以看到D点比B点更加接近方程(x - 2) * (x - 2) = 0的根(x = 2)
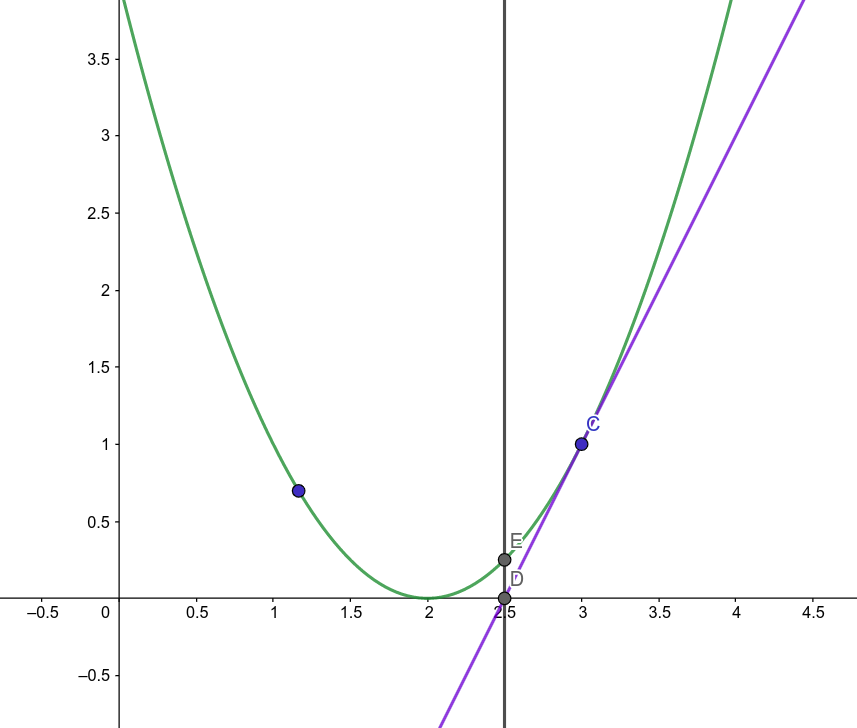
3. 在曲线上做E点的切线,交X轴与F点,在F点做X轴的垂线,交曲线于G点。可以看到G点比D点更加接近方程的根
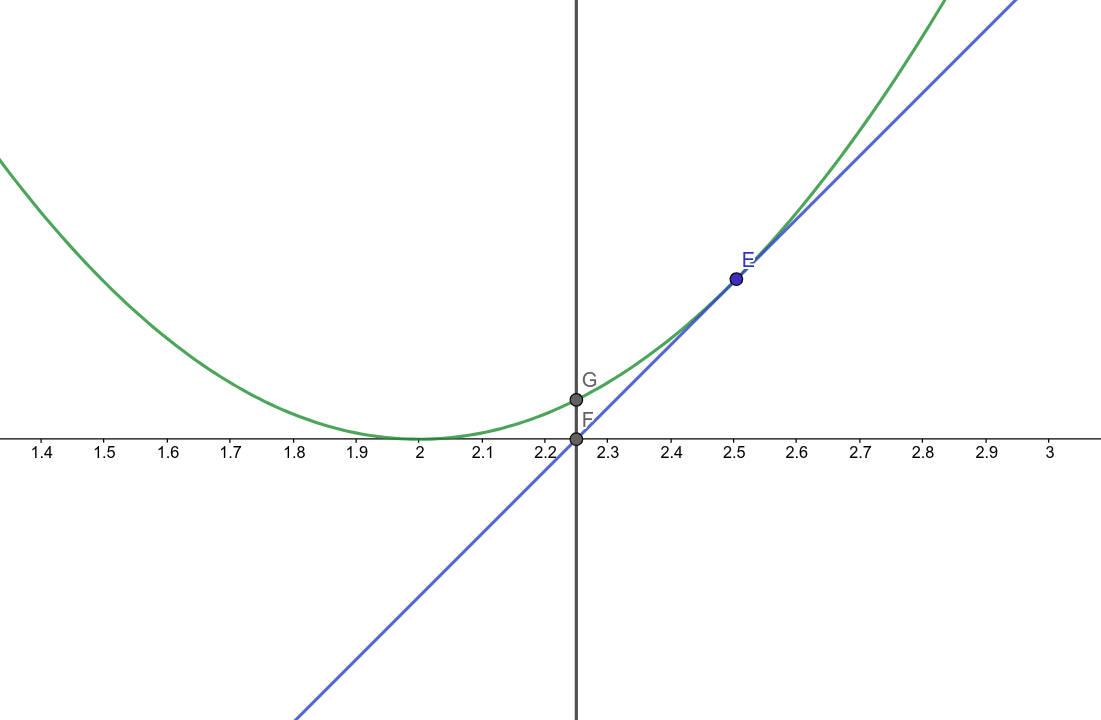
4. 按照这个方式不断迭代会离方程的根越来越近,以此得到近似根。
三、牛顿迭代法求平方根代码实现
要求是这样:输入一个数,输出其对应的平方根。
假设输入的数是 m,则其实是求一个 x 值,使其满足 x2 = m,令 f(x) = x2 - m ,其实就是求方程 f(x) = 0 的根。那么 f(x) 的导函数是 f'(x) = 2x。
那么 f(x) 函数的曲线在 (xn,xn2 - m) 处的切线的斜率是:2xn,因此切线方程是:y = 2xn (x - xn) + xn2 - m。故切线与x轴的交点是:xn+1 = (xn + m / xn ) / 2
根据牛顿迭代法,首先应该在曲线 f(x) 上任意选取一点,做切线。那么,我们直接把输入的数 m,作为选取的点的横坐标,即 x0 = m,然后根据上式进行迭代。
#include <iostream>
#include <cmath>
using namespace std;
// err 是允许的误差
const double err = 1e-8;
double NtSqrt(const double num)
{
if (num < 0)
{
return -1;
}
else
{
double root = num;
// 如果原值减去近似根的平方大于误差,继续循环
while (abs(num - root * root) >= err)
{
// 得到下一个近似根
root = (num / root + root) / 2.0;
}
return root;
}
}
int main()
{
double num;
cout << "请输入一个数: ";
cin >> num;
double ans = NtSqrt(num);
if (ans == -1)
{
cout << "负数没有平方根" << endl;
}
else
{
cout << num << " 的平方根是 " << ans << endl;
}
return 0;
}
转自: