1、最长公共子序列
对于两个子序列 S1 和 S2,找出它们最长的公共子序列。
定义一个二维数组 dp 用来存储最长公共子序列的长度,其中 dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。考虑 S1i 与 S2j 值是否相等,分为两种情况:
- 当 S1i==S2j 时,那么就能在 S1 的前 i-1 个字符与 S2 的前 j-1 个字符最长公共子序列的基础上再加上 S1i 这个值,最长公共子序列长度加 1,即 dp[i][j] = dp[i-1][j-1] + 1。
- 当 S1i != S2j 时,此时最长公共子序列为 S1 的前 i-1 个字符和 S2 的前 j 个字符最长公共子序列,或者 S1 的前 i 个字符和 S2 的前 j-1 个字符最长公共子序列,取它们的最大者,即 dp[i][j] = max{ dp[i-1][j], dp[i][j-1] }。
综上,最长公共子序列的状态转移方程为:
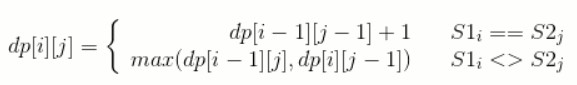
对于长度为 N 的序列 S1 和长度为 M 的序列 S2,dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。
与最长递增子序列相比,最长公共子序列有以下不同点:
- 针对的是两个序列,求它们的最长公共子序列。
- 在最长递增子序列中,dp[i] 表示以 Si 为结尾的最长递增子序列长度,子序列必须包含 Si ;在最长公共子序列中,dp[i][j] 表示 S1 中前 i 个字符与 S2 中前 j 个字符的最长公共子序列长度,不一定包含 S1i 和 S2j。
- 在求最终解时,最长公共子序列中 dp[N][M] 就是最终解,而最长递增子序列中 dp[N] 不是最终解,因为以 SN 为结尾的最长递增子序列不一定是整个序列最长递增子序列,需要遍历一遍 dp 数组找到最大者。
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
class Solution { public: int longestCommonSubsequence(string text1, string text2) { int n1 = text1.size(),n2 = text2.size(); if(n1 == 0 || n2 == 0) return 0; vector<vector<int>> dp(n1+1,vector<int>(n2+1)); for(int i = 1; i <= n1; i++) for(int j = 1; j <= n2; j++){ if(text1[i-1] == text2[j-1]) dp[i][j] = dp[i-1][j-1]+1; else dp[i][j] = max(dp[i][j-1],dp[i-1][j]); } return dp[n1][n2]; } };
2、不同的子序列:
115. 不同的子序列
给定一个字符串 S 和一个字符串 T,计算在 S 的子序列中 T 出现的个数。
一个字符串的一个子序列是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
dp[i][j] 代表 T 前 i 字符串可以由 S前 j 字符串组成最多个数.
所以动态方程:
当 S[j] == T[i] , dp[i][j] = dp[i-1][j-1] + dp[i][j-1](S中第j个字符与T第i字符对应) + (S中第j个字符与T第i个字符不对应)
当 S[j] != T[i] , dp[i][j] = dp[i][j-1] (只能S中第j个字符与T第i个字符不对应)
class Solution { public: int numDistinct(string s, string t) { int n1 = s.size(),n2 = t.size(); if(n1 == 0)return 0; if(n2 == 0) return 1; //过程中可能会越界 vector<vector<long long>> dp(n2+1,vector<long long>(n1+1)); //初始化,t = ""时,s不论为什么都为1 for(int j = 0; j <= n1;j++) dp[0][j] = 1; for(int i = 1; i <= n2;i++) for(int j = 1; j <= n1; j++) if(t[i-1] == s[j-1]) dp[i][j] = dp[i][j-1] + dp[i-1][j-1]; else dp[i][j] = dp[i][j-1]; return dp[n2][n1]; } };