这道题解法是用最大流算法打表来找规律(看见数据范围是2~10^18就应该意识到这道题是找规律题了)。
最大流算法代码(其实是微调了一下我之前写的代码就拿来用了):

#include<iostream> #include<cstdio> #include<vector> using namespace std; #define LL long long struct node { int to, val, rev;//去到的节点;剩余容量;nodeNet[to].rev为自身的数组编号 node(int to, int val, int rev) :to(to), val(val), rev(rev) {} }; int min(int a, int b) { return a < b ? a : b; } int N, M; vector<node> nodeNet[205]; vector<bool> passed(205, false); //深度优先算法求当前最短路径,返回最短路径的流量 int dfs(int from, int to, int v) { if (from == to)return v; passed[from] = true; for (int i = 0; i < nodeNet[from].size(); ++i) { node& tmp = nodeNet[from][i]; if (!passed[tmp.to] && tmp.val>0) { int d = dfs(tmp.to, to, min(v, tmp.val)); if (d > 0) { tmp.val -= d; nodeNet[tmp.to][tmp.rev].val += d; return d; } } } return 0; } void addNode(int from, int to, int val) { nodeNet[from].push_back(node(to, val, nodeNet[to].size())); nodeNet[to].push_back(node(from, 0, nodeNet[from].size() - 1)); } int getResult(int from, int to) { int res = 0; while (true) { for (int i = 0; i < passed.size(); ++i) passed[i] = false; int d = dfs(from, to, 10000000); if (d > 0)res += d; else return res; } } int main() { vector<int> res; //while (scanf("%d", &N) == 1) for(int N=2;N<51;++N) { for (int i = 0; i <= N; ++i) nodeNet[i].clear(); for (int i = 0; i < N; ++i) { for (int j = i+1; j < N; ++j) { addNode(i, j, i^j); } } int result = getResult(0, N - 1); res.push_back(result); printf("%d:%d ",N, result); } cout << endl; for (int i = 0; i < res.size() - 1; ++i) { cout << i + 2 << "间隔为:" << res[i + 1] - res[i] << endl; } system("pause"); }
打的表如下

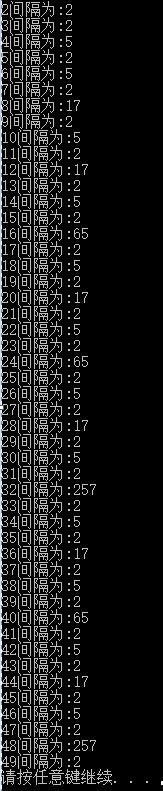
可以看出,答案数值的间隔相同的数字每隔一段距离出现一次,相同位置如果有多个数出现则出现最大的。
得知了这个规律,我们只需要找出所有间隔的数值与出现次数再全部相加即可。注意在适当的地方取模与使用long long类型以免超过取值范围。
AC代码如下:

#include<iostream> #include<cstdio> #include<map> #include<algorithm> #include<cmath> #include<vector> #define LL long long #define MOD 1000000007 #define MPower 65 using namespace std; vector<pair<LL, LL> > s; LL QPow(LL a, LL N) { long long r = 1, aa = a; while (N) { if (N & 1 == 1) r = (r * aa); N >>= 1; aa = (aa * aa) ; } return r; } int main() { LL n; while (cin >> n) { n -= 1; s.push_back({ 1,0 }); for (int i=1;;i++) { if (n >= QPow(2,i)) { if (i == 1) { pair<LL, LL> p; p.first = QPow(2, 2*(i-1)) + 1; p.second = ((n - 1) / QPow(2, i -1))%MOD; s.push_back(p); } else { pair<LL,LL> p; if (i == 2)p.first = 3; else p.first = ( s[i-1].first*4)%MOD; p.second =(1+ (n-QPow(2,i))/ QPow(2, i-1 ))%MOD; s.push_back(p); } } else break; } LL result = 1; for (int i = 0; i < s.size(); ++i) { result += (s[i].first*s[i].second); result %= MOD; } cout << result << endl; s.clear(); } //system("pause"); }
