数据结构
设计数据以何种方式组织起来并存储在计算机中。
程序 = 数据结构 + 算法
数据结构分类
线性结构:数据结构中的元素存在一对一相互关系 (节点前后有数据,前驱和后驱 链表、栈、队列、双向队列、数组等)
树结构:数据结构中的元素存在一对多的相互关系 (树(堆))
图结构:数据结构中的元素存在多对多的相互关系(图论、社交网络 微信推送好友这些都是图结构的)
顺序表:数组、列表连续存储
线性表:顺序表+链表合称线性表
栈
定义:
只能在一端进行插入或者删除操作
特点:
后进先出(LIFO)
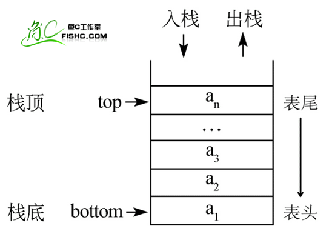
常规操作:
进栈:push
出栈:pop
取栈顶 gettop
实现栈的一些的操作:
1 #!/usr/bin/env python 2 # -*- coding:utf-8 -*- 3 4 5 class Stack(object): 6 # 定义一个空栈 7 def __init__(self): 8 self.items = [] 9 10 # 添加一个元素 11 def push(self, item): 12 self.items.append(item) 13 14 # 删除一个元素 15 def pop(self): 16 return self.items.pop() 17 18 # 返回栈顶 19 def peek(self): 20 return self.items[-1] 21 22 # 清空栈 23 def clear(self): 24 del self.items 25 26 # 判断是否为空 27 def isEmpty(self): 28 return self.items == [] 29 30 # 返回栈中元素个数 31 def size(self): 32 return len(self.items) 33 34 # 打印栈 35 def print(self): 36 print(self.items) 37 38 39 if __name__ == '__main__': 40 s = Stack() 41 print(s.isEmpty()) 42 for i in range(5): 43 s.push(i) 44 s.print() 45 s.pop() 46 s.print() 47 print(s.size()) 48 print(s.peek()) 49 s.clear()
举个例子 给定一个序列ABC,判定序列是否是它的出栈序列?
ABC ACB BCA BAC CBA都可以
CAB不可能是出栈序列,违背栈特点(ABC可以进去一个出一个)
卡特兰数:通项Cn+1 = C1Cn + C2Cn-1 + ... + CnC1
Python中实现栈的例子:创建一个列表,append() pop()pop不能带参数,删除并取出的是最后一元素
队列/双向队列
定义:
队列:
仅允许在列表的一端进行插入,另一端进行删除操作
进行插入的一端称为队尾(rear),插入动作称为进队或入队
进行删除的一端称为对头(front),删除动作称为出队
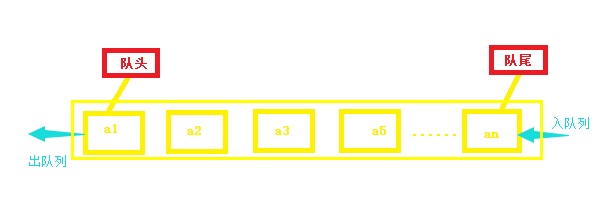
双向队列:
队列的两端都允许进行进队和出队操作

特点:
先进先出(FIFO)
队列的实现:
1 初步设想:列表+两个下标指针 2 创建一个列表和两变量,front指向队首,rear指向队尾,初始时:front rear都为0 3 进队操作:元素写到li[rear]的位置,rear自加1 4 出队操作:返回li[front]的元素,front自减1
这样实现的缺点(浪费大量空间)

改进方式:将队列的队尾和队首连接起来,这样成了一个环形队列
环形队列的实现原理:
1 当队尾指针rear==Maxsize+1,再前进一个位置就自动到0 2 实现方式:求余数 3 队首指针前进1:front = (front+1)%Maxsize 4 队尾指针前进1:rear = (reart+1)%Maxsize 5 队空条件:rear == front 6 队满条件:(rear+1)%Maxsize == front
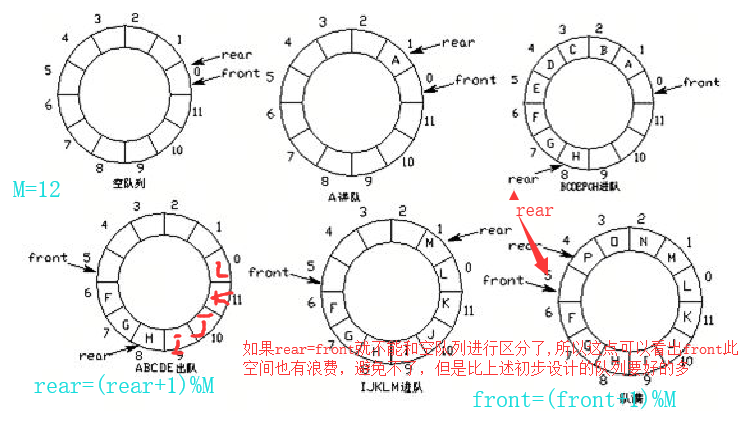
实现队列:
Python内置模块
1 #!/usr/bin/env python 2 # -*- coding:utf-8 -*- 3 4 5 # 多线程用queue 6 import queue 7 # 跟线程进程无关用deque 8 from collections import deque 9 q = deque() # 双向队列 10 # 进队 11 q.append(1) 12 q.append(2) 13 q.append(3) 14 q.appendleft(0) 15 # print(q.pop()) # 右边出去 16 print(q.popleft()) # 出队左边出 17 18 # 队列实现linux上head和tail 19 print(deque( 20 open('test', 'r', encoding='utf8'), 21 maxlen=5))
自己简单实现
1 #!/usr/bin/env python 2 # -*- coding:utf-8 -*- 3 4 5 class Queue(object): 6 # 定义一个空队列 7 def __init__(self): 8 self.items = [] 9 10 # 队列(只能在队尾)添加一个元素 11 def enqueue(self, item): 12 self.items.append(item) 13 14 # 删除队列(只能在对头)一个元素 15 def dequeue(self): 16 self.items.pop(0) 17 18 # 判断队列是否为空 19 def isEmpty(self): 20 return self.items == [] 21 22 # 清空队列 23 def clear(self): 24 del self.items # 该队列就不存在了,而不是清空元素 25 26 # 返回队列项的数量 27 def size(self): 28 return len(self.items) 29 30 # 打印队列 31 def print(self): 32 print(self.items) 33 34 35 if __name__ == '__main__': 36 q = Queue() 37 print(q.isEmpty()) 38 for i in range(5): 39 q.enqueue(i) 40 print(q.size()) 41 q.print() 42 q.dequeue() 43 q.print() 44 q.clear() 45 print(q)
两个栈实现队列
进队:1号栈进栈
出队:2号栈出栈,如果2号栈空,就去1号栈依次出栈并放在2号栈
1 1号: 2 [1,2,3,4,5,6] 3 2号 4 [4,5,6] 5 [1,2,3]->6,5,4 6 []->6,5,4,3,2,1
1 class Queue: 2 def __init__(self): 3 self.stack1 = [] 4 self.stack2 = [] 5 6 def push(self, node): 7 self.stack1.append(node) 8 9 def pop(self): 10 if self.stack1 == []: 11 return None 12 else: 13 for i in range(len(self.stack1)): 14 self.stack2.append(self.stack1.pop()) 15 out = self.stack2.pop() 16 for j in range(len(self.stack2)): 17 self.stack1.append(self.stack2.pop()) 18 return out 19 20 21 if __name__ == '__main__': 22 times = 5 23 testList = list(range(times)) 24 testQueue = Queue() 25 for i in range(times): 26 testQueue.push(testList[i]) 27 print(testList) 28 for i in range(times): 29 a = testQueue.pop() 30 print(a, ',', end='')
链表
定义
通过各个节点之间的相互连接,最终串联成一个链表
单链表
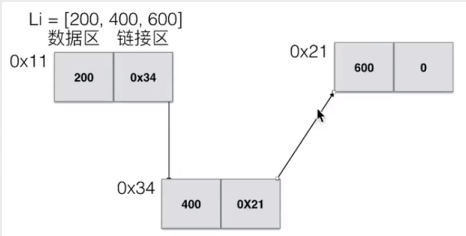
特性
链表中每一个元素都是一个对象,每个对象称之为一个节点,包含有数据域key和指向下一个节点的指针next
链表的出现
大多数原因可能因为顺序表(列表)插入删除慢,要对里边的元素进行挪动,时间复杂度被提高了
变量标识本质
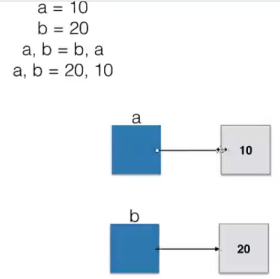
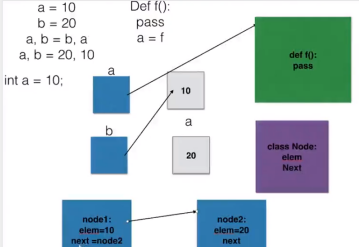
单链表的操作
1 is_empty 2 length 3 travel 遍历整个链表 4 add 5 append 6 insert 指定位置添加元素 7 remove 8 search 查找节点是否存在
遍历
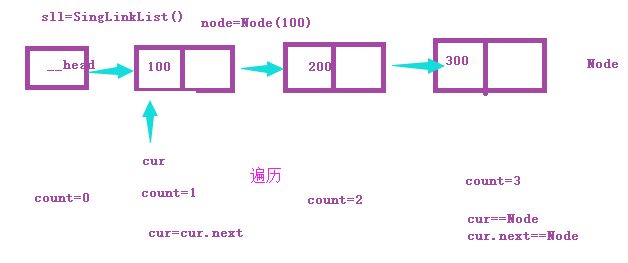
头插法
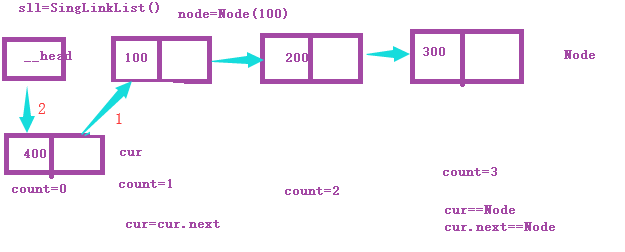
尾插法
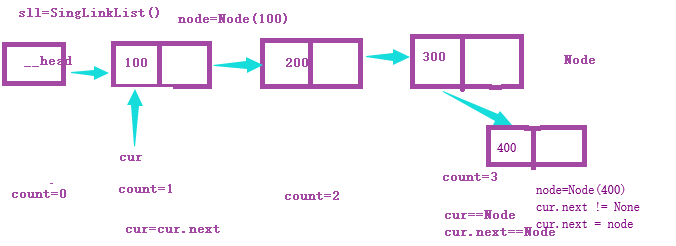
上边画图有点点问题,就是应该是第三个节点的链接区指向400节点的数据区才合适(画图没注意到)
插入
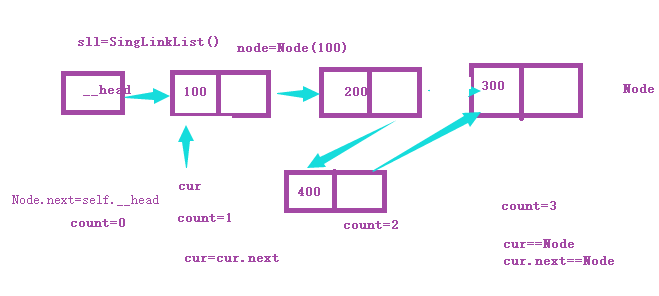
1 #!/usr/bin/env python 2 # -*- coding:utf-8 -*- 3 4 5 class Node(object): 6 """节点类""" 7 def __init__(self, elem): 8 # 数据区 9 self.elem = elem 10 # 链表区 11 self.next = None 12 13 14 class SingleLinkList(object): 15 """单链表""" 16 17 def __init__(self, node=None): 18 self.__head = node 19 20 def is_empty(self): 21 """判断链表是否为空""" 22 return self.__head == None 23 24 def length(self): 25 """链表长度""" 26 # cur游标 27 cur = self.__head 28 count = 0 # 刚好可以包含空链表的特殊情况 29 while cur != None: 30 count += 1 31 cur = cur.next 32 return count 33 34 def travel(self): 35 """遍历整个链表""" 36 cur = self.__head 37 while cur != None: 38 print(cur.elem, end=" ") 39 cur = cur.next 40 41 def add(self, item): 42 """链表头部添加元素 头插法""" 43 # 能够处理原有链表是空链表 44 node = Node(item) 45 # 新建的node节点的链表区指向头节点 46 node.next = self.__head 47 self.__head = node 48 49 def append(self, item): 50 """链表尾部追加元素 尾插法""" 51 node = Node(item) 52 if self.is_empty(): 53 self.__head = node 54 else: 55 cur = self.__head 56 while cur.next != None: 57 cur = cur.next 58 cur.next = node 59 60 def insert(self, pos, item): 61 """ 62 指定位置添加元素 63 :param pos 从0开始 64 """ 65 # 小于0我认为头插法 66 if pos <= 0: 67 self.add(item) 68 elif pos > self.length() - 1: 69 self.append(item) 70 else: 71 pre = self.__head 72 count = 0 73 while count < (pos - 1): 74 count += 1 75 pre = pre.next 76 # 当循环退出之后,pre指向pos-1位置 77 node = Node(item) 78 node.next = pre.next 79 pre.next = node 80 81 def remove(self, item): 82 """删除节点""" 83 # 创建双游标 84 cur = self.__head 85 pre = None # 是cur游标的前驱位置 86 while cur != None: 87 if cur.elem == item: 88 # 先判断删除的节点是否是头节点 89 # 头节点 直接指向头节点下节点 90 if cur == self.__head: 91 self.__head = cur.next 92 else: 93 # 包含尾节点的特殊情况了 94 pre.next = cur.next 95 break 96 else: 97 pre = cur 98 cur = cur.next 99 return -1 100 101 def search(self, item): 102 """查找节点是否存在""" 103 cur = self.__head 104 while cur != None: # 如果条件cur.next != None这样可能会漏掉cur节点 105 if cur.elem == item: 106 return True 107 else: 108 cur = cur.next 109 return False
哈希表
直接寻址
当关键字的全局u比较小时,直接寻址是一种简单而有效的方法
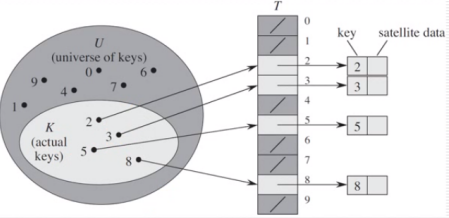
直接寻址的缺点:
当域u很大时,消耗大量内存 U很大,key很少
无法处理关键字不是数字的情况
哈希
直接寻址表:key为k的元素放到k位置上
改进直接寻址表:
构建大小为m的寻指表T
key为k的元素放到h(k)位置上
h(k)是一个函数,将域u映射到表T[0,1,2,3...,m-1]
哈希表定义
一种线性表的存储结构。哈希表由一个直接寻址表和一个哈希函数组成,哈希函数h(k)将元素关键字k作为自变量,返回元素的存储下标
常见哈希函数
除法哈希 h(k)=k mod m
乘法哈希 h(k)=floor(m(kA mod 1)) 0<A<1
解决哈希冲突
线性探查:如果位置i被占用,探查i+1, i+2.....

二次探查:如果位置i被占用,探查i+1^2,i-1^2,i+2^2,i-2^2.....

二度哈希:有n个哈希函数,但是用第一个哈希函数h1发生冲突,则尝试使用h2,h3......

拉链法:哈希表每个位置都连接一个链表,当冲突发生时,冲突的元素被加到该位置链表的最后
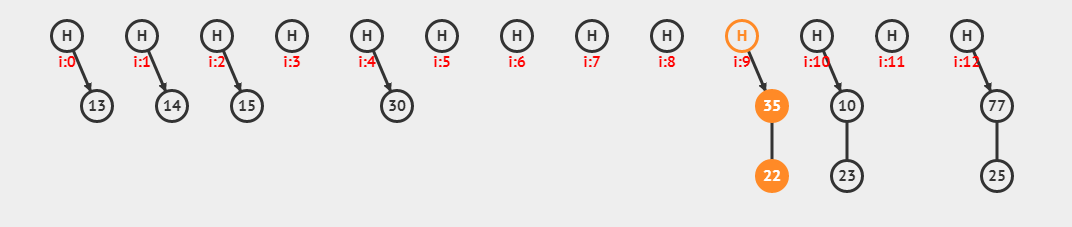
装载因子:n/m n代表元素个数 m链表大小
Python 字典和集合都是哈希表来实现的
哈希的运用:
1.哈希表,不同的key对应的值应该是平均分配(哈希函数)
2.md5摘要算法 如果判断两个文件是不是相同的(两个文件大小2G),可以用但不一定正确,如果存在哈希冲突(2G 500T),但是概率太小了,假如有30位2**30那么2**31次方就有可能有冲突,单向的算法,但是目前用的最多的就是SHA-2系列
树
见https://www.cnblogs.com/Alexephor/p/11379263.html
二叉树
定义
将二叉树的节点定义为一个对象,节点之间通过类似链表的连接方式来连接
二叉树的遍历
1 #!/usr/bin/env python 2 # -*- coding:utf-8 -*- 3 4 5 class BiTreeNode(object): 6 """ 7 二叉树定义 8 """ 9 10 def __init__(self, data): 11 self.data = data 12 self.lchild = None 13 self.rchild = None 14 15 16 class BST(object): 17 """ 18 二叉搜索树 19 """ 20 21 def __init__(self, li): 22 self.root = None 23 # 把列表转成二叉树 24 if li: 25 for val in li: 26 self.insert(val) 27 28 def insert(self, key): 29 """ 30 我这里只存的key,当然也可以把key的值存起来 31 :param key: 32 :return: 33 """ 34 if not self.root: 35 self.root = BiTreeNode(key) 36 else: 37 p = self.root 38 while p: 39 if key < p.data: # key存储在左子树 40 if p.lchild: # 如果左子树有节点,往左子树走 41 p = p.lchild 42 else: # 若左子树为空,就插入到左孩子的位置 43 p.lchild = BiTreeNode(key) 44 break 45 elif key > p.data: # 若key > p.data 46 if p.rchild: 47 p = p.rchild 48 else: 49 p.rchild = BiTreeNode(key) 50 break 51 else: # 不考虑key==p.data 字典的key唯一的嘛 也不可能相同 52 break 53 54 def traverse(self): 55 def in_order(root): 56 if root: 57 in_order(root.lchild) 58 print(root.data, end=',') 59 in_order(root.rchild) 60 in_order(self.root) 61 62 def query(self, key): 63 p = self.root 64 while p: 65 if key < p.data: 66 p = p.lchild 67 elif key > p.data: 68 p = p.rchild 69 else: 70 return True 71 return False 72 73 74 tree = BST([5, 4, 1, 4, 9, 6, 3, 2]) 75 tree.traverse() 76 print(tree.query(1)) 77 a = BiTreeNode('A') 78 b = BiTreeNode('B') 79 c = BiTreeNode('C') 80 d = BiTreeNode('D') 81 e = BiTreeNode('E') 82 f = BiTreeNode('F') 83 g = BiTreeNode('G') 84 85 e.lchild = a 86 e.rchild = g 87 a.rchild = c 88 c.lchild = b 89 c.rchild = d 90 g.rchild = f 91 92 root = e 93 94 95 def pre_order(root): 96 """ 97 前序遍历 98 :param root: 根节点 99 :return: 100 """ 101 if root: 102 print(root.data, end='') 103 pre_order(root.lchild) 104 pre_order(root.rchild) 105 106 107 def in_order(root): 108 """ 109 中序遍历 110 :param root: 根节点 111 :return: 112 """ 113 if root: 114 in_order(root.lchild) 115 print(root.data, end='') 116 in_order(root.rchild) 117 118 119 def last_order(root): 120 """ 121 后序遍历 122 :param root: 根节点 123 :return: 124 """ 125 if root: 126 last_order(root.lchild) 127 print(root.data, end='') 128 last_order(root.rchild) 129 130 131 def level_order(root): 132 from collections import deque 133 """ 134 层次遍历 135 :param root: 根节点 136 :return: 137 """ 138 q = deque() 139 q.append(root) 140 while len(q) > 0: # 不是空队 141 x = q.popleft() 142 print(x.data, end='') 143 if x.lchild: 144 q.append(x.lchild) 145 if x.rchild: 146 q.append(x.rchild) 147 148 # pre_order(root) 149 # in_order(root) 150 # last_order(root) 151 # level_order(root)
创建树的图
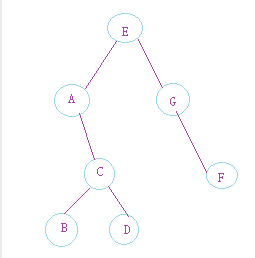
深度优先(代码p107)
前序遍历找根:EACBDGF
中序遍历找左右孩子:ABCDEGF
后序遍历也定根:BDCAFGE
进出栈思想推出序列
广度优先
队列思想推出序列
层次遍历:EAGCFBD
二叉搜索树
定义
是一棵二叉树,且满足:设x是二叉树的一个节点,如果y是x的左子树的一个节点,那么y.key<=x.key;如果y是x右子树的一个节点,那么y.key>=x.key
二叉搜索树的创建(代码p16)
二叉搜索树的遍历(中序遍历)
二叉搜索树的查询/插入/删除
删除三种情况
- 如果要删除的节点是叶子节点:直接删除
- 如果要删除节点只有一个孩子:将此节点的父亲与孩子连接,然后删除该节点
- 如果要删除的节点有两孩子:将其右子树的最小节点(该节点最多有一个右孩子)删除,并替换当前节点
二叉搜索树的效率
平均情况下,二叉搜索树进行搜索的时间复杂度为O(logn)
最坏的情况下,二叉搜索树可能非常偏斜
解决方式:
随机插入
AVL树
AVL树
是一棵自平衡的二叉搜索树
性质:根的左右子树的高度之差的绝对值不能超过1
根的左右子树都是平衡二叉树
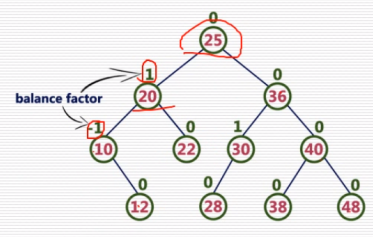
持续更新中..................