统计学习方法第二版学习笔记（一）

第1章 统计学习及监督学习概论

1.1统计学习

1. 统计学习是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科。
2. 统计学习一般包括监督学习、无监督学习、强化学习等。有时候还包括半监督学习、主动学习。
3. 统计学习方法可以概括如下：

　　从给定的、有限的、用于学习的训练数据集合出发，假设数据是独立同分布产生的；并且假设要学习的模型属于某个函数的集合，称为假设空间；应用某个评价准则，从假设空间中选取一个最优模型，使它对已知的训练数据及未知的测试数据在给定的评价标准下有最优的预测；最优模型的选取由算法实现。

　　这样统计学习方法包括模型的假设空间、模型选择的准则以及模型学习的算法。称其为统计学习方法的三要素，简称为模型、策略和算法。

　　实现统计学习方法的步骤如下：

• 得到一个有限的训练数据集合；
• 确定包含所有可能的模型的假设空间，即学习模型的集合；
• 确定模型选择的准则，即学习的策略；
• 实现求解最优模型的算法，即学习的算法；
• 通过学习方法选择最优模型；
• 利用学习的最优模型对新数据进行预测或分析。

1.2统计学习的分类

1.2.1基本分类

1. 监督学习是指从标注数据中学习预测模型的机器学习问题。监督学习的本质是学习输入到输出的映射的统计规律。依据输入输出变量的不同类型，预测任务可分为：输入变量与输出变量均为连续变量的回归问题；输出变量为有限个离散变量的分类问题；输入变量与输出变量均为变量序列的标注问题。
2. 无监督学习是指从无标注数据中学习预测模型的机器学习问题。预测模型表示数据的类别、转换或概率，以实现对数据的聚类、降维或概率估计。
3. 强化学习是指智能系统在与环境的连续互动中学习最优行为策略的机器学习问题。假设智能系统与环境的互动基于马尔可夫决策过程，智能系统能得到的是与环境互动得到的数据序列。强化学习的本质是学习最优的序贯决策。
4. 半监督学习是指利用标注数据和未标注数据学习预测模型的机器学习问题。半监督学习旨在利用未标注数据中的信息，辅助标注数据，进行监督学习，以较低的成本达到较好的学习效果。
5. 主动学习是指机器不断主动给出示例让教师进行标注，以较小的标注代价，达到较好的学习效果。

1.2.2按模型分类

　　1、概率模型与非概率模型

　　监督学习中概率模型是生成模型，非概率模型是判别模型。本书中的决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯混合模型是概率模型。感知机、支持向量机、k近邻、AdaBoost、k均值、潜在语义分析、神经网络是非概率模型。Logistic回归既可看作是概率模型，也可以看作是非概率模型。

　　2、线性模型与非线性模型

　　3、参数化模型与非参数化模型

1.2.3按算法分类

　　在线学习、批量学习

1.2.4按技巧分类

　　1、贝叶斯学习

　　公式（1.4）：

　　参考：https://zhuanlan.zhihu.com/p/107944440

　　

　　2、核方法

1.3统计学习方法三要素

　　1、统计学习方法由模型、策略、算法三要素组成，可简单表示为：

　　方法=模型+策略+算法

　　2、模型就是所要学习的条件概率分布或决策函数

　　

 　　3、策略：考虑按照什么样的准则学习或选择最优的模型（风险最小化策略）

　　模型的预测值与真实值差距越小，则表示模型越好，对应的参数向量越合适。所使用的判别标准就是所谓的“策略”。

　　为此引入损失函数、风险函数的概念：

　　损失函数度量模型一次预测的好坏，风险函数度量平均意义下模型预测的好坏。

　　常用的损失函数有：

• 0-1损失函数
• 平方损失函数
• 绝对损失函数
• 对数损失函数

　　风险函数或期望损失：

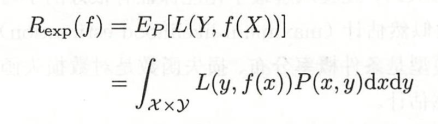
　　经验风险或经验损失：

 

 　　期望风险Rexp是模型关于联合分布的期望损失，经验风险Remp是模型关于训练样本集的平均损失。

　　依据大数定律，当样本容量N趋于无穷时，经验风险Remp趋于期望风险Rexp。故此常用经验风险估计期望风险。但是由于现实中训练样本数目有限，甚至很小，所以用经验风险估计期望风险常常并不理想，要对经验风险进行一定的矫正。监督学习常用的两个基本矫正策略为：经验风险最小化和结构风险最小化。

　　

 　　（常用方法增加样本量、增加正则项、交叉验证等）

　　4、算法

　　统计学习基于训练数据集，根据学习策略，从假设空间中选择最优模型，最后需要考虑用什么样的计算方法求解最优模型。

　　此时，统计学习问题归结为最优化问题，统计学习的算法称为求解最优化问题的算法。最优化问题通常无法找到显式的解析解，此时需要用数值计算方法求解。如何保证找到全局最优解，并使求解规程非常高效，就成为一个重要问题。

1.5正则化与交叉验证

1.5.1正则化

　　1、从拉格朗日乘子法（KKT条件）及贝叶斯最大后验概率角度理解L1、L2正则化。

　　参考：https://blog.csdn.net/hong__fang/article/details/78281200

　　2、对于线性回归问题，L1正则化又称为“LASSO回归”，L2正则化称为“岭回归”。

　　3、L1正则化使模型的非零参数尽量地少（使得较多的参数归零），L2正则化则尽量把参数保留下来（使高阶项趋于零）。

课后题解答参考：

https://zhuanlan.zhihu.com/p/89249562

笔记参考：

https://zhuanlan.zhihu.com/c_1213397558586257408